1.7. Применение теоремы о циркуляции вектора магнитной индукции. Магнитное поле внутри прямого проводника с током

В качестве примера применения теоремы о циркуляции вектора магнитной индукции для расчета индукции магнитного поля рассмотрим магнитное поле постоянного тока, текущего в бесконечно длинном прямом проводнике цилиндрической формы радиуса R. Замкнутый контур выберем в виде окружности радиуса r, лежащей в плоскости, перпендикулярной оси проводника, и с центром на этой оси (рис. 18).  Пусть направление обхода контура связано с направлением тока правилом правого винта. Из осевой симметрии следует, что во всех точках, равноудаленных от оси проводника с током, индукция магнитного поля одинакова. Проекция вектора магнитной индукции на направление элементарного перемещения совпадает по величине с магнитной индукцией во всех точках замкнутого контура. Т аким образом, для циркуляции вектора магнитной индукции получаем , (1.12) где   – проекция вектора магнитной индукции на направление элементарного перемещения  . Если  , то по закону полного тока: . (1.13) Из сравнения (1.12) и (1.13) следует , что совпадает с ранее полученной формулой (1.6). Если  , в предположении равномерного распределения тока по сечению проводника, по закону полного тока , (1.14) где   – площадь, охватываемая контуром l; j – плотность тока. Из сравнения (1.12) и (1.14) следует . 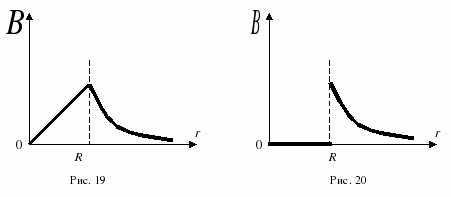(1.15) На графике (рис. 19) показана зависимость индукции магнитного поля от расстояния до оси прямого проводника с током. Рассмотрим полый проводник цилиндрической формы в виде трубы, вдоль стенки которой течет постоянный ток. Пусть ^ R – радиус трубы. Замкнутый контур выберем также в форме окружности радиуса r с центром на оси проводника. Пусть  . В этом случае контур не охватывает ток и . (1.16) Из сравнения (1.12) и (1.16) следует, что магнитное поле внутри полого проводника с током отсутствует. На рис. 20 представлена зависимость величины индукции магнитного поля в некоторой точке от ее расстояния до оси прямого полого проводника с током. 1.8. Магнитное поле соленоида Соленоид представляет собой тонкий провод, навитый плотно (виток к витку) на цилиндрический каркас. На рис. 21 представлено схематическое изображение бесконечно длинного соленоида диаметром D. Будем считать, чт о намотка выполнена плотно, соседние витки прилегают друг к другу и по соленоиду течет ток силойI. Выясним, как направлен вектор   в различных точках магнитного поля соленоида. Для этого рассмотрим два любых элемента тока   и  , равных по величине и расположенных симметрично относительно плоскости сечения АА, перпендикулярной к оси соленоида (рис. 22). Элементы   и   перпендикулярны плоскости рисунка. По закону Био–Савара–Лапласа рассматриваемые элементы тока создадут в каждой точке сечения АА магнитные поля, индукции которых   и   равны по величине, а их результирующий вектор   параллелен оси соленоида. Этот вывод справедлив для любой пары одинаковых элементов тока соленоида, расположенных симметрично относительно плоскости сечения АА. Из принципа суперпозиции следует, что линии индукции магнитного поля бесконечно длинного соленоида, если оно отлично от нуля, должны быть параллельны оси соленоида как внутри, так и вне соленоида. Теперь докажем, что в точках, находящихся на расстоянии, много большем диаметра соленоида с плотной намоткой витков, магнитное поле равно нулю. Для этого рассмотрим два равных по модулю элемента тока   и  , расположенных симметрично относительно оси соленоида (рис. 23). В точках, достаточно удален ных от соленоида, для которых  , по закону Био–Савара–Лапласа магнитные индукции   и   будут равны и противоположны по направлению с хорошей степенью точности. Этот вывод справедлив для любой пары одинаковых элементов тока соленоида, расположенных симметрично относительно оси соленоида. Из принципа суперпозиции следует, что в достаточно удаленных от соленоида точках магнитное поле отсутствует. Дл я вычисления величины индукции магнитного поля соленоида применим теорему о циркуляции вектора   по замкнутому контуру. Выберем контур прямоугольной формы, две стороны которого параллельны, а другие две стороны перпендикулярны оси соленоида (рис. 24, а, б). Пусть участок контура   находится от соленоида на расстоянии, много большем его диаметра, а участок  , параллельный оси соленоида, расположен в первом случае внутри соленоида (рис. 24, а) и во втором случае вне соленоида (рис. 24, б). Циркуляция вектора   на контуре 1–2–3–4 равна сумме линейных интегралов: . Из соображений симметрии и так как линии магнитной индукции должны быть параллельны оси соленоида, как было показано выше,   во всех точках участка  . На участках контура   и     перпендикулярен элементарному перемещению. Следовательно,   во всех точках участков   и  . Точки участка   находятся на расстоянии, много большем диаметра соленоида, и в них, как отмечалось ранее, можно считать   с хорошей степенью точности. Таким образом, , (1.17) где   – длина участка  . Согласно теореме о циркуляции в случае, когда контур охватывает ток (рис. 24, а), , (1.18) где n – плотность намотки (число витков на единицу длины соленоида),  а n  – число витков на длине  . Если контур не охватывает ток (рис. 24, б), то . (1.19) Из сравнения (1.17) с (1.18) и (1.19) следует, что магнитное поле внутри бесконечно длинного соленоида однородно. Магнитная индукция поля равна . (1.20)

Тепловое излучение. Характеристики теплового излучения спектральная плотность энергетической светимости, монохроматический коэффициент поглощения

Тепловое излучение, температурное излучение, электромагнитное излучение, испускаемое веществом и возникающее за счёт его внутренней энергии (в отличие, например, от люминесценции, возникающей за счёт внешних источников энергии). Т. и. имеетсплошной спектр, положение максимума которого зависит от температуры вещества. С её повышением возрастает общая энергия испускаемого Т. и., а максимум перемещается в область малых длин волн. Т. и. испускают, например, поверхность накалённого металла, земная атмосфера и т. д.

Т. и. возникает в условиях детального равновесия в веществе (см. Детального равновесия принцип) для всех безызлучательных процессов, то есть для различных типов столкновений частиц в газах и плазме, для обмена энергиями электронного и колебательного движений в твёрдых телах и т. д. Равновесное состояние вещества в каждой точке пространства — состояние локального термодинамического равновесия (ЛТР) — при этом характеризуется значением температуры, от которого и зависит Т. и. вещества в данной точке.

В общем случае системы тел, для которой осуществляется лишь ЛТР и различные точки которой имеют различные температуры, Т. и. не находится в термодинамическом равновесии с веществом. Горячие тела испускают больше, чем поглощают, а более холодные — наоборот. Происходит перенос излучения от более горячих тел к более холодным. Для поддержания стационарного состояния, при котором сохраняется распределение температуры в системе, необходим подвод теплоты к более горячим телам и отвод от более холодных; это может осуществляться как в природных условиях (например, в атмосфере Земли), так и искусственно (например, в лампах накаливания).

При полном термодинамическом равновесии все части системы тел имеют одну температуру и энергия Т. и., испускаемого каждым телом, компенсируется энергией поглощаемого этим телом Т. и. др. тел. В этом случае Т. и. находится в термодинамическом равновесии с веществом и называется равновесным излучением (равновесным является Т. и. абсолютно чёрного тела). Спектр равновесного излучения не зависит от природы вещества и определяется Планка законом излучения.

Для Т. и. нагретых тел в общем случае справедлив Кирхгофа закон излучения, связывающий их испускательную и поглощательную способности с испускательной способностью абсолютно чёрного тела.

При наличии ЛТР, применяя законы излучения Кирхгофа и Планка к испусканию и поглощению Т. и. в газах и плазме, можно изучать процессы переноса излучения. Такое рассмотрение широко используется в астрофизике, в частности в теории звёздных атмосфер.

Количественной характеристикой теплового излучения служит спектральная плот­ность энергетической светимости (излучательности) тела — мощность излучения с еди­ницы площади поверхности тела в интервале частот единичной ширины:

где d  — энергия электромагнитного излучения, испускаемого за единицу времени (мощность излучения) с единицы площади поверхности тела в интервале частот от  до +d.

Единица спектральной плотности энергетической светимости (R_,T) — джоуль на метр в квадрате (Дж/м²).

Записанную формулу можно представить в виде функции длины волны:

Так как c=, то

где знак минус указывает на то, что с возрастанием одной из величин ( или ) другая величина убывает. Поэтому в дальнейшем знак минус будем опускать. Таким образом,

                                                                       (197.1)

С помощью формулы (197.1) можно перейти от R_,T  к R_,T и наоборот.

Зная спектральную плотность энергетической светимости, можно вычислить интег­ральную энергетическую светимость (интегральную излучательность)(ее называют про­сто энергетической светимостью тела), просуммировав по всем частотам:

                                                       (197.2)

Способность тел поглощать падающее на них излучение характеризуется спект­ральной поглощательной способностью показывающей, какая доля энергии, приносимой за единицу времени на единицу площади поверхности тела падающими на нее электромагнитными волнами с частотами от  до +d, поглощается телом. Спектральная поглощательная способность — величина безразмерная. Величины R_,T  и А_,T зависят от природы тела, его термодинамической температуры и при этом различаются для излучений с различными частотами. Поэтому эти величины относят к определенным Т и (вернее, к достаточно узкому интервалу частот от  до +d).

Тело, способное поглощать полностью при любой температуре все падающее на него излучение любой частоты, называется черным. Следовательно, спектральная поглощательная способность черного тела для всех частот и температур тождественно равна единице ( ). Абсолютно черных тел в природе нет, однако такие тела, как сажа, платиновая чернь, черный бархат и некоторые другие, в определенном интервале частот по своим свойствам близки к ним.

Идеальной моделью черного тела является замкнутая полость с небольшим отвер­стием О, внутренняя поверхность которой зачернена (рис. 286). Луч света, попавший внутрь такой полости, испытывает многократные отражения от стенок, в результате чего интенсивность вышедшего излучения оказывается практически равной нулю. Опыт показывает, что при размере отверстия, меньшего 0,1 диаметра полости, пада­ющее излучение всех частот полностью поглощается. Вследствие этого открытые окна домов со стороны улицы кажутся черными, хотя внутри комнат достаточно светло из-за отражения света от стен.

Наряду с понятием черного тела используют понятие серого тела — тела, поглощательная способность которого меньше единицы, но одинакова для всех частот и зависит только от температуры, материала и состояния поверхности тела. Таким образом, для серого тела  =A_T = const<l.

Исследование теплового излучения сыграло важную роль в создании квантовой теории света, поэтому необходимо рассмотреть законы, которым оно подчиняется.

Ток смещения. Система уравнений Макс¬велла. Относительность электрических и магнитных полей. Электромагнитная волна.

Согласно Максвеллу, если всякое переменное магнитное поле возбуждает в окружа­ющем пространстве вихревое электрическое поле, то должно существовать и обратное явление: всякое изменение электрического поля должно вызывать появление в окружающем пространстве вихревого магнитного поля. Для установления количественных соотношений между изменяющимся электрическим полем и вызываемым им магнит­ным полем Максвелл ввел в рассмотрение так называемый ток смещения.

Рассмотрим цепь переменного тока, содержащую конденсатор (рис. 196). Между обкладками заряжающегося и разряжающегося конденсатора имеется переменное электрическое поле, поэтому, согласно Максвеллу, через конденсатор «протекают» токи смещения, причем в тех участках, где отсутствуют проводники.

Найдем количественную связь между изменяющимся электрическим и вызываемым им магнитным полями. По Максвеллу, переменное электрическое поле в конденсаторе в каждый момент времени создает такое магнитное поле, как если бы между обклад­ками конденсатора существовал ток смещения, равный току в подводящих проводах. Тогда можно утверждать, что токи проводимости (I) и смещения (I_см) равны: I_см =I.

Ток проводимости вблизи обкладок конденсатора

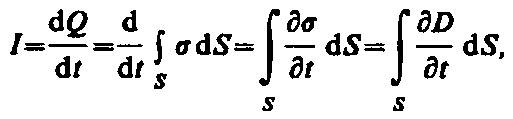(138.1)

(поверхностная плотность заряда  на обкладках равна электрическому смещению D в конденсаторе (см. (92.1)). Подынтегральное выражение в (138.1) можно рассматривать как частный случай скалярного произведения когда и dS взаимно параллельны. Поэтому для общего случая можно записать

Сравнивая это выражение с (см. (96.2)), имеем

(138.2)

Выражение (138.2) и было названо Максвеллом плотностью тока смещения.

Рассмотрим, каково же направление векторов плотностей токов проводимости и смещения j и j_см. При зарядке конденсатора (рис. 197, а) через проводник, соединя­ющий обкладки, ток течет от правой обкладки к левой; поле в конденсаторе усиливается; следовательно, >0, т. е. вектор направлен в ту же сторону, что и D. Из рисунка видно, что направления векторов и j совпадают. При разрядке конденсатора (рис. 197, б) через проводник, соединяющий обкладки, ток течет от левой обкладки к правой; поле в конденсаторе ослабляется; следовательно, <0, т. е. вектор направлен противоположно вектору D. Однако вектор направлен опять так же, как и вектор j. Из разобранных примеров следует, что направление вектора j, а следовательно, и вектора j_см, совпадает с направлением вектора , как это и следует из формулы (138.2).

Подчеркнем, что из всех физических свойств, присущих току проводимости, Макс­велл приписал току смещения лишь одно — способность создавать в окружающем пространстве магнитное поле. Таким образом, ток смещения (в вакууме или веществе) создает в окружающем пространстве магнитное поле (линии индукции магнитных полей токов смещения при зарядке и разрядке конденсатора показаны на рис. 197 штриховыми линиями).

В диэлектриках ток смещения состоит из двух слагаемых. Так как, согласно (89.2), D=₀E+P, где Е – напряженность электростатического поля, а Р — поляризованность (см. § 88), то плотность тока смещения

(138.3)

где ₀ — плотность тока смещения в вакууме, — плотность тока поляризации — тока, обусловленного упорядоченным движением электрических зарядов в ди­электрике (смещение зарядов в неполярных молекулах или поворот диполей в поляр­ных молекулах). Возбуждение магнитного поля токами поляризации правомерно, так как токи поляризации по своей природе не отличаются от токов проводимости. Однако то, что и другая часть плотности тока смещения , не связанная с движением зарядов, а обусловленная только изменением электрического поля во времени, также возбуждает магнитное поле, является принципиально новым утверждением Максвелла. Даже в вакууме всякое изменение во времени электрического поля приводит к возник­новению в окружающем пространстве магнитного поля.

Следует отметить, что название «ток смещения» является условным, а точ­нее — исторически сложившимся, так как ток смещения по своей сути — это изменя­ющееся со временем электрическое поле. Ток смещения поэтому существует не только в вакууме или диэлектриках, но и внутри проводников, по которым проходит переменный ток. Однако в данном случае он пренебрежимо мал по сравнению с током проводимости. Наличие токов смещения подтверждено экспериментально А.А. Эйхенвальдом, изучавшим магнитное поле тока поляризации, который, как следует из (138.3), является частью тока смещения.

Максвелл ввел понятие полного тока, равного сумме токов проводимости (а также конвекционных токов) и смещения. Плотность полного тока

Введя понятия тока смещения и полного тока, Максвелл по-новому подошел к рас­смотрению замкнутости цепей переменного тока. Полный ток в них всегда замкнут, т. е. на концах проводника обрывается лишь ток проводимости, а в диэлектрике (вакууме) между концами проводника имеется ток смещения, который замыкает ток проводимости.

Максвелл обобщил теорему о циркуляции вектора Н (см. (133.10)), введя в ее правую часть полный ток I_полн = j_полнdS сквозь поверхность S, натянутую на замкнутый контур L. Тогда обобщенная теорема о циркуляции вектора Н запишется в виде

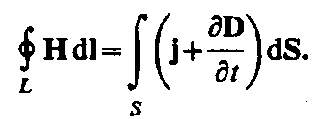(138.4)

Выражение (138.4) справедливо всегда, свидетельством чего является полное соответст­вие теории и опыта.