Формула 1 — Потенциал

 Потенциал электрического поля это энергетическая характеристика поля. Он представляет собой работу которую нужно совершить против сил электрического поля для того чтобы переместить единичный положительный точечный заряд находящийся на бесконечности в данную точку поля.

Измеряется потенциал электрического поля в вольтах.

В случае если поле создается несколькими зарядами, которые расположены в произвольном порядке. Потенциал в данной точке такого поля будет представлять собой алгебраическую сумму всех потенциалов, которые создают заряды каждый в отдельности. Это так называемый принцип суперпозиции.

Формула 2 — суммарный потенциал разных зарядов

 Допустим, что в электрическом поле заряд перемещается из точки "a" в точку "b". Работа совершается против силы электрического поля. Соответственно потенциалы в этих точках будут отличаться.

Формула 3 — Работа в электрическом поле

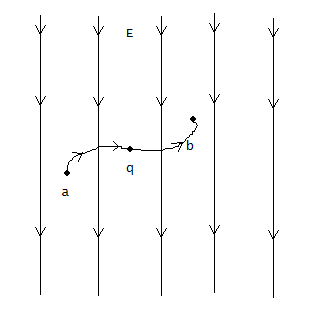
Рисунок 1 — перемещение заряда в электрическом поле

  Разность потенциалов двух точек поля будет равна одному Вольту, если для того чтобы переместить заряд в один кулон между ними необходимо совершить работу в один джоуль.

 Если заряды имеют одинаковые знаки, то потенциальная энергия взаимодействия между ними будет положительна. В этом случае заряды отталкиваются друг от друга.

Для разноименных зарядов энергия взаимодействия будет отрицательна. Заряды в этом случае будут, притягивается друг к другу.

Для установления связи между силовой характеристикой электрического поля - напряжённостью и его энергетической характеристикой - потенциалом рассмотрим элементарную работу сил электрического поля на бесконечно малом перемещении точечного заряда q: dA = q E dl, эта же работа равна убыли потенциальной энергии заряда q: dA = - dW_п = - q d , где d - изменение потенциала электрического поля на длине перемещения dl. Приравнивая правые части выражений, получаем: E dl = -d или в декартовой системе координат

E_x dx + E_y dy + E_z dz = -d ,      (1.8)

где E_x, E_y, E_z - проекции вектора напряженности на оси системы координат. Поскольку выражение (1.8) представляет собой полный дифференциал, то для проекций вектора напряженности имеем

откуда

.

Стоящее в скобках выражение является градиентом потенциала j, т. е.

E = - grad = -Ñ .

Напряжённость в какой-либо точке электрического поля равна градиенту потенциала в этой точке, взятому с обратным знаком. Знак «минус» указывает, что напряженность E направлена в сторону убывания потенциала.

Рассмотрим электрическое поле, создаваемое положительным точечным зарядом q (рис. 1.6). Потенциал поля в точке М, положение которой определяется радиус-вектором r, равен = q / 4pe₀er. Направление радиус-вектора r совпадает с направлением вектора напряженности E, а градиент потенциала направлен в противоположную сторону. Проекция градиента на направление радиус-вектора

.

Проекция же градиента потенциала на направление вектора t, перпендикулярного вектору r, равна

,

т. е. в этом направлении потенциал электрического поля является постоянной величиной ( = const).

В рассмотренном случае направление вектора r совпадает с направлением рис. 1.6 силовых линий. Обобщая полученный результат, можно утверждать, что во всех точках кривой, ортогональной к силовым линиям, потенциал электрического поля одинаков. Геометрическим местом точек с одинаковым потенциалом является эквипотенциальная поверхность, ортогональная к силовым линиям.

рис. 1.7

При графическом изображении электрических полей часто используют эквипотенциальные поверхности. Обычно эквипотенциали проводят таким образом, чтобы разность потенциалов между любыми двумя эквипотенциальными поверхностями была одинакова. На рис. 1.7 приведена двухмерная картина электрического поля. Силовые линии показаны сплошными линиями, эквипотенциали - штриховыми.

Подобное изображение позволяет сказать, в какую сторону направлен вектор напряжённости электрического поля; где напряжённость больше, где меньше; куда начнёт двигаться электрический заряд, помещённый в ту или иную точку поля. Так как все точки эквипотенциальной поверхности находятся при одинаковом потенциале, то перемещение заряда вдоль нее не требует работы. Это значит, что сила, действующая на заряд, все время перпендикулярна перемещению.

Радиоактивность. α, β, γ – распады.

Радиоактивностью называется способность атомного ядра самопроизвольно распадаться с испусканием частиц.     Радиоактивный распад ядра возможен тогда, когда он энергетически выгоден, т.е. сопровождается выделением энергии. Условием этого является превышение массы M исходного ядра суммы масс m_iпродуктов распада, которому соответствует неравенство M > ∑m_i. Это условие является необходимым, но не всегда достаточным. Распад может быть запрещен другими законами сохранения – сохранения момента количества движения, электрического заряда, барионного заряда и т.д.    Радиоактивный распад характеризуется временем жизни радиоактивного изотопа, типом испускаемых частиц, их энергиями.    Основными видами радиоактивного распада являются:

• α-распад – испускание атомным ядром α-частицы;

• β-распад – испускание атомным ядром электрона и антинейтрино, позитрона и нейтрино, поглощение ядром атомного электрона с испусканием нейтрино;

• γ-распад – испускание атомным ядром γ-квантов;

• спонтанное деление – распад атомного ядра на два осколка сравнимой массы.

Поток вектора. Теорема Гаусса и ее применение к расчету электриче­ских полей.

Потоком вектора магнитной индукции (магнитным потоком) через площадку dS называ­ется скалярная физическая величина, равная где B_n=В cos  —проекция вектора В на направление нормали к площадке dS ( — угол между векторами n и В), dS=dSn — вектор, модуль которого равен dS, а направление его совпадает с направлением нормали n к площадке. Поток вектора В может быть как положительным, так и отрицательным в зависимости от знака cos  (определяется выбором положительного направления нормали n). Поток вектора В связывают с контуром, по которому течет ток. В таком случае положительное направление нормали к контуру нами уже определено : оно связывается с током правилом правого винта. Таким образом, магнитный поток, создаваемый контуром через поверхность, ограниченную им самим, всегда положителен. Для однородного поля и плоской поверхности, расположенной перпендикулярно вектору В, B_n=B=const и

Из этой формулы определяется единица магнитного потока вебер (Вб): 1 Вб — маг­нитный поток, проходящий сквозь плоскую поверхность площадью 1 м², расположен­ную перпендикулярно однородному магнитному полю, индукция которого равна 1 Тл (1 Вб=1 Тлм²). Теорема Гаусса для поля В: поток вектора магнитной индукции сквозь любую замкнутую поверхность равен нулю:

(120.3)

Эта теорема отражает факт отсутствия магнитных зарядов, вследствие чего линии магнитной индукции не имеют ни начала, ни конца и являются замкнутыми.

Итак, для потоков векторов В и Е сквозь замкнутую поверхность в вихревом и потенциальном полях получаются различные выражения. В качестве примера рассчитаем поток вектора В сквозь соленоид. Магнитная индукция однородного поля внутри соленоида с сердечником с магнитной проницае­мостью , согласно (119.2), равна

Магнитный поток сквозь один виток соленоида площадью S равен

а полный магнитный поток, сцепленный со всеми витками соленоида и называемый потокосцеплением,

(120.4)

Сторонние силы

С торонние силы – силы, вызывающие разделение зарядов внутри источника тока. Сторонние силы – силы неэлектрического происхождения. 0ни возникают за счёт химических реакций, за счёт механической энергии и др.

Электродвижущая сила источника тока — э.д.с. ( ε ), единица измерения — 1 В (Вольт). Э.д.с.- физическая величина, равная работе, совершаемой сторонними силами при перемещении по электрической цепи единичного положительного заряда: ε = Аст./q .

4. Сопротивление проводника — R, единица измерения — 1 Ом. Под действием электрического поля в вакууме свободные заряды двигались бы ускоренно. В веществе они движутся в среднем равномерно, т.к. часть энергии отдают частицам вещества при столкновениях.

Теория утверждает, что энергия упорядоченного движения зарядов рассеивается на искажениях кристаллической решетки. Исходя из природы электрического сопротивления, следует, что R = ρ*l/S , где l — длина проводника, S — площадь поперечного сечения, ρ — коэффициент пропорциональности, названный удельным сопротивлением материала. Эта формула хорошо подтверждается на опыте. Взаимодействие частиц проводника с движущимися в токе зарядами зависит от хаотического движения частиц, т.е. от температуры проводника. Известно, что ρ = ρ0(1 +Δ t) , R = R0(1 +Δt)

Коэффициент k называется температурным коэффициентом сопротивления: k = (R — R0)/R0*t .

Для химически чистых металлов K > 0 и равно 1/273 К-1. Для сплавов температурные коэффициенты имеют меньшее значение. Зависимость (t) для металлов линейная:

В 1911 году открыто явление сверхпроводимости, заключающееся в том, что при температуре, близкой к абсолютному нулю, сопротивление некоторых металлов падает скачком до нуля.

У некоторых веществ (например, у электролитов и полупроводников) удельное сопротивление с ростом температуры уменьшается, что объясняется ростом концентрации свободных зарядов. Величина, обратная удельному сопротивлению, называется удельной электрической проводимостью G G = 1/ρ .

5. Напряжение — U , единица измерения — 1 В. Напряжение — физическая величина, равная работе, совершаемой сторонними и электрическими силами при перемещении единичного положительного заряда. U = (Aст.+ Аэл.)/q .

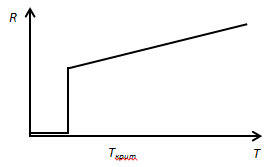
Зависимость сопротивления проводника от температуры. Сверхпроводники

С увеличением температуры сопротивление проводника возрастает по линейному закону

где R₀ - сопротивление при t=0° С; R- сопротивление при температуре t, α - термический коэффициент сопротивления, показывает как меняется сопротивление проводника при изменении температуры на 1 градус. Для чистых металлов при не очень низких температурах  , т.е. можно записать

При определенных температурах (0,14-20 К),     называемых «критическими» сопротивление проводника резко уменьшается до 0 и металл переходит в сверхпроводящее состояние. Впервые в 1911 г. Это обнаружил Камерлинг-Оннес для ртути. В 1987 г. разработаны керамики,  переходящие в сверхпроводящее состояние при температурах превышающих 100 К, так называемые высокотемпературные сверхпроводники - ВТСП.

Строение атома. Спектры. Спектральные закономерности излучения атома водорода. Формула Бальмера.

Атом состоит из массивного положительно заряженного ядра и маленьких отрицательно заряженных электронов, которые вращаются по орбиталям вокруг ядра. Ядро в свою очередь, состоит из положительных протонов и нейтронов, имеющих нулевой заряд. 

Атомные спектры, оптические спектры, получающиеся при испускании или поглощении электромагнитного излучения свободными или слабо связанными атомами (например, в газах или парах). Являются линейчатыми, то есть состоят из отдельных спектральных линий, характеризуемых частотой излучения v, которая соответствует квантовому переходу между уровнями энергии E_i и E_k атома согласно соотношению: hv = E_i-E_k где h-постоянная Планка.

Спектральные закономерности 

В середине XVIII в. Г. Кирхгоф обнаружил: свечение газов дает четко выраженные дискретные линии.

Швейцарский препо­даватель И. Бальмер эмпирически вывел формулу для спектра водорода (1885):  , где п—любое целое число >2, т. е. п=3, 4, 5 и т.д.

Теорема о циркуляции вектора магнитной индукции. Применение к расчету поля соленоида