Постулаты Бора

Первая попытка построить качественно новую — квантовую — теорию атома была предпринята в 1913 г. датским физиком Нильсом Бором (1885—1962). Он поставил перед собой цель связать в единое целое эмпирические закономерности линейчатых спектров, ядерную модель атома Резерфорда и квантовый характер излучения и погло­щения света. В основу своей теории Бор положил два постулата.

Первый постулат Бора (постулат стационарных состояний): в атоме существуют стационарные (не изменяющиеся со временем) состояния, в которых он не излучает энергии. Стационарным состояниям атома соответствуют стационарные орбиты, по которым движутся электроны. Движение электронов по стационарным орбитам не сопровождается излучением электромагнитных волн.

В стационарном состоянии атома электрон, двигаясь по круговой орбите, должен иметь дискретные квантованные значения момента импульса, удовлетворяющие условию

(210.1)

где т_е — масса электрона, v — его скорость по n-й орбите радиуса r_n, ћ = h/(2).

Втором постулат Бора (правило частот): при переходе электрона с одной стационар­ной орбиты на другую излучается (поглощается) один фотон с энергией

(210.2)

равной разности энергий соответствующих стационарных состояний (Е_n и E_m — соот­ветственно энергии стационарных состояний атома до и после излучения (поглоще­ния)). При Е_m<Е_n происходит излучение фотона (переход атома из состояния с боль­шей энергией в состояние с меньшей энергией, т. е. переход электрона с более удален­ной от ядра орбиты на более близлежащую), при Е_m>Е_n — его поглощение (переход атома в состояние с большей энергией, т. е. переход электрона на более удаленную от ядра орбиту). Набор возможных дискретных частот  = (E_n—E_m)/h квантовых перехо­дов и определяет линейчатый спектр атома.

Бо́ровская моде́ль а́тома (Моде́ль Бо́ра) — полуклассическая модель атома, предложенная Нильсом Бором в 1913 г. За основу он взял планетарную модель атома, выдвинутую Резерфордом. Однако, с точки зрения классической электродинамики, электрон в модели Резерфорда, двигаясь вокруг ядра, должен был бы излучатьнепрерывно и очень быстро, потеряв энергию, упасть на ядро. Чтобы преодолеть эту проблему, Бор ввел допущение, суть которого заключается в том, что электроны в атоме могут двигаться только по определенным (стационарным) орбитам, находясь на которых они не излучают, а излучение или поглощение происходит только в момент перехода с одной орбиты на другую. Причем стационарными являются лишь те орбиты, при движении по которым момент количества движения электрона равен целому числу постоянных Планка

Работа и мощность тока. Законы Ома и Джоуля - Ленца в интегральной и ло­кальной (дифференциальной) форме. Законы последовательного и параллельного соединения резисторов

РАБОТА ПОСТОЯННОГО ТОКА

Работа тока - это работа электрического поля по переносу электрических зарядов вдоль проводника; Работа тока на участке цепи равна произведению силы тока, напряжения и времени, в течение которого работа совершалась.

Применяя формулу закона Ома для участка цепи, можно записать несколько вариантов формулы для расчета работы тока:

По закону сохранения энергии:

работа равна изменению энергии участка цепи, поэтому выделяемая проводником энергия равна работе тока.

В системе СИ:

ЗАКОН ДЖОУЛЯ -ЛЕНЦА

При прохождениии тока по проводнику проводник нагревается, и происходит теплообмен с окружающей средой, т.е. проводник отдает теплоту окружающим его телам.

Количество теплоты, выделяемое проводником с током в окружающую среду, равно произведению квадрата силы тока, сопротивления проводника и времени прохождения тока по проводнику.

По закону сохранения энергии количество теплоты, выделяемое проводником численно равно работе, которую совершает протекающий по проводнику ток за это же время.

В системе СИ:

[Q] = 1 Дж

МОЩНОСТЬ ПОСТОЯННОГО ТОКА - отношение работы тока за время t к этому интервалу времени.

В системе СИ:

Последовательное и параллельное соединения проводников

Последовательным называется такое соединение резисторов, когда конец одного проводника соединяется с началом другого и т.д. (рис. 1). При последовательном соединении сила тока на любом участке электрической цепи одинакова. Это объясняется тем, что заряды не могут накапливаться в узлах цепи. Их накопление привело бы к изменению напряженности электрического поля, а следовательно, и к изменению силы тока. Поэтому

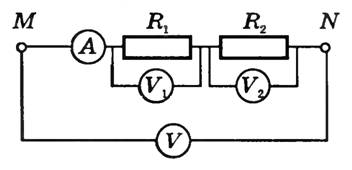Рис. 1

Амперметр А измеряет силу тока в цепи и обладает малым внутренним сопротивлением (RA → 0).

Включенные вольтметры V1 и V2 измеряют напряжение U1 и U2 на сопротивлениях R1 и R2. Вольтметр V измеряет подведенное к клеммам Μ и N напряжение U. Вольтметры показывают, что при последовательном соединении напряжение U равно сумме напряжений на отдельных участках цепи:

Применяя закон Ома для каждого участка цепи, получим:

где R — общее сопротивление последовательно соединенной цепи. Подставляя U, U1, U2 в формулу (1), имеем

Сопротивление цепи, состоящей из n последовательно соединенных резисторов, равно сумме сопротивлений этих резисторов:

Если сопротивления отдельных резисторов равны между собой, т.е. R1 = R2 = ... = Rn, то общее сопротивление этих резисторов при последовательном соединении в n раз больше сопротивления одного резистора: R = nR1.

При последовательном соединении резисторов справедливо соотношение  , т.е. напряжения на резисторах прямо пропорциональны сопротивлениям.

Параллельным называется такое соединение резисторов, когда одни концы всех резисторов соединены в один узел, другие концы — в другой узел (рис. 2). Узлом называется точка разветвленной цепи, в которой сходятся более двух проводников. При параллельном соединении резисторов к точкам Μ и N подключен вольтметр. Он показывает, что напряжения на отдельных участках цепи с сопротивлениями R1 и R2 равны. Это объясняется тем, что работа сил стационарного электрического поля не зависит от формы траектории:

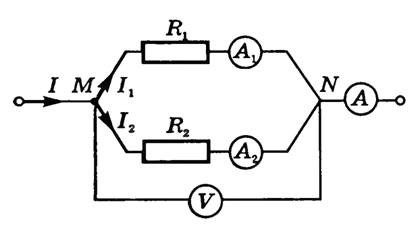Рис. 2

Амперметр показывает, что сила тока I в неразветвленной части цепи равна сумме сил токов I1 и I2 в параллельно соединенных проводниках R1 и R2:

Это вытекает и из закона сохранения электрического заряда. Применим закон Ома для отдельных участков цепи и всей цепи с общим сопротивлением R:

Подставляя I, I1 и I2 в формулу (2), получим:

Величина, обратная сопротивлению цепи, состоящей из n параллельно соединенных резисторов, равна сумме величин, обратных сопротивлениям этих резисторов:

Если сопротивления всех n параллельно соединенных резисторов одинаковы и равны R1 то  . Откуда  .

Сопротивление цепи, состоящей из n одинаковых параллельно соединенных резисторов, в n раз меньше сопротивления каждого из них.

При параллельном соединении резисторов справедливо соотношение  , т.е. силы токов в ветвях параллельно соединенной цепи обратно пропорциональны сопротивлениям ветвей.

Работа силы и ее выражение через криволинейный интеграл. Мощность.

Чтобы охарактеризовать скорость совершения работы, вводят понятие мощности:

(11.3)

За время dt сила F совершает работу Fdr, и мощность, развиваемая этой силой, в данный момент времени

т. е. равна скалярному произведению вектора силы на вектор скорости, с которой движется точка приложения этой силы; N — величина скалярная.

Единица мощности — ватт (Вт): 1 Вт — мощность, при которой за время 1 с совершается работа 1 Дж (1 Вт = 1 Дж/с). Изменение механического движения тела вызывается силами, действующими на него со стороны других тел. Чтобы количественно характеризовать процесс обмена энергией между взаимодействующими телами, в механике вводится понятие работы силы. Работа силы на участке траектории от точки 1 до точки 2 равна алгебраической сумме элементарных работ на отдельных бесконечно малых участках пути. Эта сумма приводится к интегралу

(11.2)

Для вычисления этого интеграла надо знать зависимость силы F_s, от пути s вдоль траектории 1—2. Пусть эта зависимость представлена графически (рис. 14), тогда искомая работа А определяется на графике площадью заштрихованной фигуры. Если, например, тело движется прямолинейно, сила F=const и =const, то получим

где s — пройденный телом путь

Работа электрического поля. Циркуляция электрического поля. Потен­циал. Связь потенциала с напряженностью электростатического поля.

Элементарная работа, совершаемая силой F при перемещении точечного электрического заряда из одной точки электростатического поля в другую на отрезке пути , по определению равна

где - угол между вектором силы F и направлением движения . Если работа совершается внешними силами, то dA0. Интегрируя последнее выражение, получим, что работа против сил поля при перемещении пробного заряда из точки “а” в точку “b” будет равна

где - кулоновская сила, действующая на пробный заряд в каждой точке поля с напряженностью Е. Тогда работа

Пусть заряд перемещается в поле заряда q из точки “а”, удалённой от q на расстоянии в точку “b”, удаленную от q на расстоянии (рис 1.12).

Как видно из рисунка тогда получим

Как было сказано выше, работа сил электростатического поля, совершаемая против внешних сил, равна по величине и противоположна по знаку работе внешних сил, следовательно

(13.16)

Циркуляция вектора напряженности электрического поля. Работа, совершаемая силами электрического поля при перемещении единичного положительного заряда по замкнутому контуру длиной l, определяется как циркуляция вектора напряженности электрического поля:

Так как для замкнутого пути положения начальной и конечной точек перемещения заряда совпадают, то работа сил электрического поля на замкнутом пути равна нулю, а значит, равна нулю и циркуляция вектора напряженности, т.е.

.

Равенство нулю означает, что силы электрического поля являются силами консервативными, а само поле - потенциальным.

Потенциал электрического поля представляет собой отношение потенциальной энергии к заряду. Как известно электрическое поле является потенциальным. Следовательно, любое тело находящиеся в этом поле обладает потенциальной энергией. Любая работа, которая будет совершаться полем, будет происходить за счет уменьшения потенциальной энергии.