Абсолютно черное тело

- понятие теории теплового излучения, означающее тело, к-рое полностью поглощает любое падающее на его поверхность эл.-магн. излучение, независимо от темп-ры этого тела. Т. о., для А. ч. т. поглощательная способность (отношение поглощённой энергии к энергии падающегоизлучения) равна 1 при излучениях всех частот, направлений распространения и поляризаций.

Плотность энергии и спектральный состав излучения, испускаемого единицей поверхности А. ч. т. (излучения А. ч. т., чёрного излучени я), зависят только от его темп-ры, но не от природы излучающего вещества. Излучение А. ч. т. может находиться в равновесии с веществом (при равенстве потоков излучения, испускаемого и поглощаемого А. ч. т., имеющим опре-дел. темп-ру), посвоим характеристикам такое излучение представляет излучение равновесное и подчиняется Планка закону излучения, определяющему ис-пускат. способность и энергетич. яркость А. ч. т. (пропорциональные плотности энергии равновесного излучения). Понятие А. ч. т. введено в 1859 Г. Р. Кирхгофом (G. R. Kirchhoff), установившим связь между испускат. и поглощат.способностями тела, находящегося в равновесии с излучением при определ. темп-ре (см. Кирхгофа закон излучения). А. ч. т. в природе не существует, однако хорошим приближением к нему является устройство, состоящее из замкнутой полости, внутр. поверхность к-рой нагрета до темп-ры Т, с отверстием, малым по сравнению с размерами полости. Внутри полости устанавливается практически полное равновесие излучения с веществом, и плотность энергии выходящего из отверстия излучения очень мало отличается от равновесной. Подобные устройства, с высокой точностью моделирующие А. ч. т., применяют в качестве световых эталонов, используют при измерениях высоких темп-р (см. Пирометрия оптическая).

КИРХГОФА ЗАКОН ИЗЛУЧЕНИЯ

закон, утверждающий, что отношение испускат. способности e(l, Т) тел к их поглощат. способности а(l, Т) не зависит от природы излучающего тела, равно излучат. способности абсолютно чёрного тела e0(l, T) и зависит от длины волны излучения l и абс. темп-ры Т:

(e(l, T))/(a(l, T))=e0(l,T).

Ф-ция e0(l, T) в явном виде даётся Планка законом излучения.

К. з. и. явл. одним из осн. законов теплового излучения и не распространяется на др. виды излучения. Он установлен нем. физиком Г. Р. Кирхгофом (G. R. Kirchhoff) в 1859 на основании второго начала термодинамики и затем подтверждён экспериментально. Согласно К. з. и., тело, к-рое при данной темп-ре лучше поглощает излучение, должно интенсивнее излучать. Напр., при накаливании платиновой пластинки, часть к-рой покрыта платиновой чернью, её чёрный конец (поглощат. способность к-рого близка к единице) светится ярче, чем светлый.

Вина закон излучения, закон распределения энергии в спектре равновесного излучения (излучения абсолютно чёрного тела) в зависимости от температуры. Этот закон теоретически выведен В. Вином (1893). Согласно В. з. и., плотность энергии излучения u_v, соответствующая частоте излучения v, зависит от v и абсолютной температуры Т следующим образом:  u_v = v³f (v/T),

  где f — некоторая функция отношения v/T. Из этого закона можно получить Вина закон смещения. В 1896 Вин получил для u_vследующую зависимость:   

  (c₁ и c₂ — постоянные коэффициенты). Этот закон представляет собой предельный случай Планка закона излучения и справедлив при больших частотах излучения (малых длинах волн).

Закон Стефана-Больцмана

Теоретическое объяснение законов излучения абсолютно черного тела имело огромное значение в истории физики – оно привело к понятию квантов энергии. Долгое время попытки получить теоретически вид функции f(w,Т) не давали общего решения задачи. Стефан (1879), анализируя экспериментальные данные, пришел к выводу, что энергетическая светимость R любого тела пропорциональна четвертой степени абсолютной температуры. Однако последующие более точные измерения показали ошибочность его выводов. Больцман (1884), исходя из термодинамических соображений, получил теоретически для энергетической светимости абсолютно черного тела следующее значение:

Таким образом, заключение, к которому Стефан пришел для нечерных тел (с абсолютно черными телами он не экспериментировал), оказалось справедливым лишь для абсолютно черных тел.

Рэлея — Джинса закон излучения, закон, выражающий распределение энергии в спектре абсолютно чёрного тела в зависимости от температуры. Р. — Д. з. и. может быть записан в виде:  ,

где u_n — плотность излучения, соответствующая частоте n, с — скорость света, Т — абсолютная температура, k — Больцмана постоянная.

Р. — Д. з. и. был выведен в 1900 Дж. У. Рэлеем из классических представлений о равномерном распределении энергии по степеням свободы. В 1905—09 Дж. Джинс, применив методы классической статистической механики к стационарным волнам в полости, пришёл к той же формуле, что и Рэлей. Р. — Д. з. и. хорошо согласуется с экспериментом лишь для малых n (в длинноволновой области спектра). С ростом n энергия излучения по Р. — Д. з. и. должна неограниченно расти, достигая чрезвычайно больших значений в далёкой ультрафиолетовой и ещё более коротковолновой областях спектра (так называемая ультрафиолетовая катастрофа), но это противоречит опыту. Распределение энергии в спектре абсолютно чёрного тела, справедливое для всего спектра, получается только на основе квантовых представлений (см. Планка закон излучения). Р. — Д. з. и. является частным случаем закона Планка для малых n; его применяют вместо закона Планка при рассмотрении достаточно длинноволнового излучения и в тех случаях, когда не требуется высокая точность вычислений.

Атомное ядро. Строение атомных ядер. Энергия связи. Ядерные силы. Ядерные ре­акции

Атомное ядро – центральная и очень компактная часть атома, в которой сосредоточена практически вся его масса и весь положительный электрический заряд. Ядро, удерживая вблизи себя кулоновскими силами электроны в количестве, компенсирующем его положительный заряд, образует нейтральный атом. Большинство ядер имеют форму близкую к сферической и диаметр ≈ 10^-12 см, что на четыре порядка меньше диаметра атома (10^-8 см). Плотность вещества в ядре – около 230 млн.тонн/см³.      Атомное ядро было открыто в 1911 г. в результате серии экспериментов по рассеянию альфа-частиц тонкими золотыми и платиновыми фольгами, выполненных в Кембридже (Англия) под руководством Э. Резерфорда. В 1932 г. после открытия там же Дж. Чедвиком нейтрона стало ясно, что ядро состоит из протонов и нейтронов  (В. Гейзенберг, Д.Д. Иваненко, Э. Майорана).  Атом состоит из ядра и окружающего его электронного "облака". Находящиеся в электронном облаке электроны несут отрицательныйэлектрический заряд. Протоны, входящие в состав ядра, несут положительный заряд.В любом атоме число протонов в ядре в точности равно числу электронов в электронном облаке, поэтому атом в целом – нейтральная частица, не несущая заряда. Атом может потерять один или несколько электронов или наоборот – захватить чужие электроны. В этом случае атом приобретает положительный или отрицательный заряд и называется ионом. Практически вся масса атома сосредоточена в его ядре, так как масса электрона составляет всего лишь 1/1836 часть массы протона. Плотность вещества в ядре фантастически велика – порядка 10¹³ - 10¹⁴ г/см³. Спичечный коробок, наполненный веществом такой плотности, весил бы 2,5 миллиарда тонн! Внешние размеры атома – это размеры гораздо менее плотного электронного облака, которое примерно в 100000 раз больше диаметра ядра. Кроме протонов, в состав ядра большинства атомов входят нейтроны, не несущие никакого заряда. Масса нейтрона практически не отличается от массы протона. Вместе протоны и нейтроны называются нуклонами (от латинского nucleus – ядро). Электроны, протоны и нейтроны являются главными "строительными деталями" атомов и называются субатомными частицами. Их заряды и массы в кг и в специальных “атомных” единицах массы (а.е.м.) показаны в таблице 2-1.

Энергия связи ядра – минимальная энергия, необходимая для того, чтобы разделить ядро на составляющие его нуклоны (протоны и нейтроны). Ядро – система связанных нуклонов, состоящая из Z протонов (масса протона в свободном состоянии m_p) и N нейтронов (масса нейтрона в свободном состоянии m_n). Для того, чтобы разделить ядро на составные нуклоны, нужно затратить определенную минимальную энергию W, называемую энергией связи. При этом покоящееся ядро с массой М переходит в совокупность свободных покоящихся протонов и нейтронов с суммарной массой Zm_p + Nm_n. Энергия покоящегося ядра Мс². Энергия освобождённых покоящихся нуклонов (Zm_{p +} Nm_n)с². В соответствии с законом сохранения энергии Мс² + W = (Zm_p + Nm_n)с². Или W = (Zm_p + Nm_n)с² - Мс². Поскольку W > 0, то М < (Zm_p + Nm_n), т.е. масса, начального ядра, в котором нуклоны связаны, меньше суммы масс свободных нуклонов, входящих в его состав.     W растёт с увеличением числа А нуклонов в ядре (А = Z + N). Удобно иметь дело с удельной энергией связи ε = W/A, т.е. средней энергией связи, приходящейся на один нуклон. Для большинства ядер ε ≈ 8 МэВ (1 МэВ = 1.6·10^-13 Дж). Для разрыва химической связи нужна энергия в 10⁶ раз меньше.

Между нуклонами в ядре действуют силы притяжения – ядерные силы. Ядерные силы относятся, наряду с гравитационными и электромагнитными, к числу так называемыхфундаментальных сил природы. В квантовой механике вместо понятия “сила” чаще используется понятие “взаимодействие”. Синонимом выражения “ядерные силы” является выражение “сильное взаимодействие”. Этим выражением подчеркивается тот факт, что ядерные силы гораздо более “сильные”, чем электромагнитные и тем более гравитационные. Ведь ядерные силы удерживают в ядре одноименно заряженные протоны, которые по закону Кулона отталкиваются, и незаряженные нейтроны. Не будь ядерных сил, ядра разлетелись бы на отдельные нуклоны. Таким образом, ядерные силы самые “сильные” в природе. Я́дерная реа́кция — это процесс взаимодействия атомного ядра с другим ядром или элементарной частицей, сопровождающийся изменением состава и структуры ядра и выделением большого количества энергии. Впервые ядерную реакцию наблюдал Резерфордв 1919 году, бомбардируя α-частицами ядра атомов азота, она была зафиксирована по появлению вторичных ионизирующих частиц, имеющих пробег в газе больше пробега α-частиц и идентифицированных как протоны. Впоследствии с помощью камеры Вильсонабыли получены фотографии этого процесса.

По механизму взаимодействия ядерные реакции делятся на два вида:

• реакции с образованием составного ядра, это двухстадийный процесс, протекающий при не очень большой кинетической энергиисталкивающихся частиц (примерно до 10 МэВ).

• прямые ядерные реакции, проходящие за ядерное время, необходимое для того, чтобы частица пересекла ядро. Главным образом такой механизм проявляется при больших энергиях бомбардирующих частиц.

Взаимодействие параллельных проводников с током. Направление и величина сил взаимодействия.

Взаимодействие проводников с током

Если близко один к другому расположены проводники с токами одного направления, то магнитные линии этих проводников, охватывающие оба проводника, обладая свойством продольного натяжения и стремясь сократиться, будут заставлять проводники притягиваться (фиг. 100, а). Магнитные линии двух проводников с токами разных направлений в пространстве между проводниками направлены в одну сторону. Магнитные линии, имеющие одинаковое направление, обладают свойством бокового распора. Поэтому проводники с токами противоположного направления отталкиваются один от другого (фиг. 100, б). Рассмотрим взаимодействие двух параллельных проводов с токами, расположенными на расстоянии а один от другого. Пусть длина проводов равна /. Магнитная индукция, созданная током l₁ на линии расположения второго Проводника, равна:

Магнитная индукция, созданная током /₂ на линии расположения первого проводника, будет равна:

Второе начало термодинамики. Энтропия.

Появление второго начала термодинамики связано с необходимостью дать ответ на вопрос, какие процессы в природе возможны, а какие - нет. Второе начало термодинамики определяет направление протекания термодинамических процессов.Используя понятие энтропии и неравенство Клаузиуса (см. раздел 3.8), второе начало термодинамики можно сформулировать как закон возрастания энтропии замкнутой системы при необратимых процессах: любой необратимый процесс в замкнутой системе происходит так, что энтропия системы при этом возрастает Можно дать более краткую формулировку второго начала термодинамики: в процессах, происходящих в замкнутой системе, энтропия не убывает. Здесь существенно то, что речь идет о замкнутых системах, так как в незамкнутых системах энтропия может вести себя любым образом. Приведем еще две формулировки второго начала термодинамики:1) невозможен круговой процесс, единственным результатом которого является превращение теплоты, полученной от нагревателя, в эквивалентную ей работу;2) невозможен круговой процесс, единственным результатом которого является передача теплоты от менее нагретого тела к более нагретому.Понятие энтропии введено в 1865 г. Р. Клаузиусом. Для выяснения физического содержания этого понятия рассматривают отношение теплоты Q, полученной телом в изотермическом процессе, к температуре T теплоотдающего тела, называемое приведенным количеством теплоты. В термодинамике доказывается, что энтропия системы, совершающей необратимый цикл, возрастает:ΔS > 0 (3.32)

Энтропия замкнутой системы может либо возрастать (в случае необратимых процессов), либо оставаться постоянной (в случае обратимых процессов). Taк как для адиабатического процесса δQ = 0, то S = 0 и, следовательно, S = const, т. е. адиабатический обратимый процесс протекает при постоянной энтропии. Поэтому его часто называют изоэнтропийным процессом. Энтропия обладает свойством аддитивности: энтропия системы равна сумме энтропий тел, входящих в систему. Более глубокий смысл энтропии вскрывается в статистической физике: энтропия связывается с термодинамической вероятностью состояния системы.

Гипотеза Планка. Фотоны. Масса, энергия и импульс фотона.

Гипо́теза Пла́нка — гипотеза, выдвинутая 14 декабря 1900 года Максимом Планком и заключающаяся в том, что при тепловом излучении энергия испускается и поглощается не непрерывно, а отдельными квантами (порциями). Каждая такая порция-квант имеет энергию  , пропорциональную частоте ν излучения: где h или   — коэффициент пропорциональности, названный впоследствии постоянной Планка. На основе этой гипотезы он предложил теоретический вывод соотношения между температурой тела и испускаемым этим телом излучением — формулу Планка.Позднее гипотеза Планка была подтверждена экспериментально.Выдвижение этой гипотезы считается моментом рождения квантовой механики.

Фото́н — элементарная частица, квант электромагнитного излучения (в узком смысле — света). Это безмассовая частица, способная существовать в вакууме только двигаясь со скоростью света.Электрический заряд фотона также равен нулю. Фотон может находиться только в двух спиновых состояниях с проекциейспина на направление движения (спиральностью) ±1. В физике фотоны обозначаются буквой γ. Классическая электродинамика описывает фотон как электромагнитную волну с круговой правой или левой поляризацей. С точки зрения классической квантовой механики, фотону как квантовой частице свойственен корпускулярно-волновой дуализм, он проявляет одновременно свойства частицы и волны.

Фотон — безмассовая нейтральная частица. Спин фотона равен 1 (частица является бозоном), но из-за нулевой массы покоя более подходящей характеристикой является спиральность, проекция спина частицы на направление движения. Фотон может находиться только в двух спиновых состояниях со спиральностью, равной  . Этому свойству в классической электродинамикесоответствует поперечность электромагнитной волны.^[9] Массу покоя фотона считают равной нулю, основываясь на эксперименте и теоретических обоснованиях, описанных выше. Поэтому скорость фотона равна скорости света. По этой причине (не существует системы отсчёта, в которой фотон покоится)внутренняя чётность частицы не определена.^[9] Если приписать фотону наличие т. н. «релятивистской массы» (термин ныне выходит из употребления) исходя из соотношения   то она составит   Фотон — истинно нейтральная частица(тождественен своей античастице)^[49], поэтому его зарядовая чётность отрицательна и равна −1. Вследствие закона сохранения зарядовой чётности и её мультипликативности в электромагнитных процессах невозможно превращение чётного числа фотонов в нечётное и наоборот (Теорема Фарри). Фотон не имеет электрического заряда и не распадается спонтанно в вакууме, стабилен. Фотон может иметь одно из двух состояний поляризации и описывается тремя пространственными параметрами — составляющими волнового вектора, который определяет его длину волны   и направление распространения. Если энергия фотона равна  , то импульс   связан с энергией соотношением  , где   — скорость света (скорость, с которой в любой момент времени движется фотон как безмассовая частица). Для сравнения, для частиц с ненулевой массой покоя связь массы и импульса с энергией определяется формулой  , как показано в специальной теории относительности.^[55] В вакууме энергия и импульс фотона зависят только от его частоты   (или, что эквивалентно, от длины волны  ):

,

,

и, следовательно, величина импульса есть:

,

Действие маг­нитного поля на токи и заряженные частицы. Магнитный момент контура с током.

Электрический ток представляет собой упорядоченное направленное движение заряженных частиц. Поэтому действие магнитного поля на проводник с током (сила Ампера) является результатом того, что это поле действует на движущиеся внутри проводника заряженные частицы. Силу, действующую на заряженную частицу в магнитном поле, называют силой Лоренца в честь голландского физика Х. Лоренца. Найдём направление и модуль силы Лоренца F_Л с помощью закона Ампера (3.1). Пусть на прямолинейный участок проводника длиной L при силе тока в нем I, находящийся в однородном магнитном поле с индукцией В (рис.4а), действует сила Ампера F_А. Если N – число заряженных частиц, упорядоченно движущихся на этом участке проводника, то, очевидно, что сила Лоренца, F_Л равна: Найдём N, исходя из того, что сила тока I равна произведению заряда частицы q, их концентрации n, скорости их упорядоченного движения v и площади поперечного сечения проводника S: I = qnvS. (4.2)

Так как , то из (4.2) получаем следующее выражение для N:

подставляя которое в (4.1) и учитывая формулу (3.1), получим формулу для F_Л:

Если заряд положительный, то для определения направления силы Лоренца можно пользоваться правилом левой руки (рис. 4б). На движущуюся отрицательно заряженную частицу сила Лоренца действует в противоположном направлении. Сила Лоренца не совершает работы, так как её вектор перпендикулярен вектору скорости движения частицы. Сила Лоренца используется в электронно-лучевых трубках (ЭЛТ) телевизоров и мониторов, где магнитное поле позволяет отклонять электроны, летящие к экрану ЭЛТ. Заряженная частица, влетая в однородном магнитном поле, направленное перпендикулярно вектору ее скорости, начинает равномерно двигаться по окружности радиуса r, а сила Лоренца в этом случае является центростремительной силой (рис. 4в). Радиус окружности движения частиц в магнитном поле можно узнать из соотношения:

где m – масса заряженной частицы. Как следует из (4.5), r зависит от массы частицы, и это используется в масс-спектрометрах – устройствах, где анализ движения заряженных частиц в магнитном поле позволяет измерять их массы. Частицы разных знаков, влетая в магнитное поле, поворачивают в разные стороны, что даёт возможность определить знак заряда частиц.

Если заряженная частица движется в магнитном поле так, что вектор скорости v составляет с вектором магнитной индукции B угол , то траекторией движения частицы является винтовая линия (рис. 4г). Поэтому заряженная частица, влетая в магнитное поле, продолжает свое движение вдоль линий индукции этого поля. Таким же образом магнитное поле Земли защищает нас и всё живое от потоков заряженных частиц космического пространства.

Вопросы для повторения:

Как найти направление и модуль силы Лоренца?

Как действует сила Лоренца на модуль скорости заряженной частицы?

Опишите движение заряженной частицы в однородном магнитном поле, если её начальная скорость перпендикулярна линиям магнитной индукции.

 

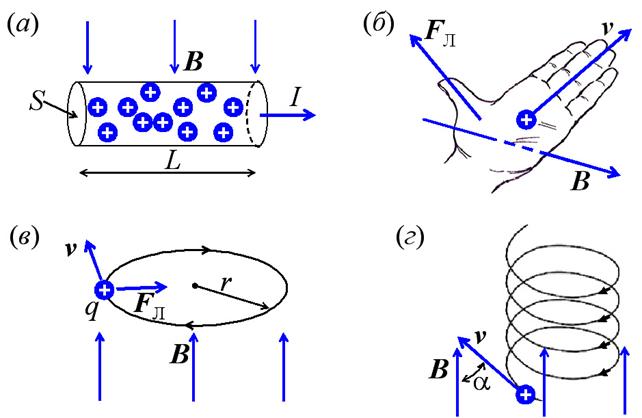
Рис. 4. (а) – к вычислению силы Лоренца; (б) – определение направления силы Лоренца с помощью правила левой руки; движение по окружности (в) и винтовой линии (г) заряженной частицы в магнитном поле.

Опыт показывает, что электрические токи взаимодействуют между собой, напрмер, токи I притягиваются, а токи I отталкиваются. Взаимодействие токов осуществляется через поле, которое называется магнитным. Следовательно, движущиеся заряды (токи ) изменяют свойства окружающего их пространства - создают в нем магнитное поле. Это поле проявляется в том, что на движущиеся в нем заряды (токи) действуют силы. Подобно тому, как для исследования электрического поля мы использовали пробный заряд, применим для исследования магнитного поля пробный ток, циркулирующий в плоском замкнутом контуре очень малых размеров . Будем называть такой контур пробным контуром.

О риентацию его в пространстве характеризует направление нормали к контуру, восстанавливаемой по правилу правого буравчика: вращаем рукоятку правого буравчика по направлению тока в контуре, тогда направление его поступательного движения даст направление нормали (см. рис. 1). Помещая пробный контур в магнитное поле, обнаружим, что поле стремится повернуть контур (нормаль) в определенном направлении. Вращающий момент, действующий на контур, зависит как от свойств магнитного поля в данной точке, так и от свойств контура. Оказывается, что максимальная величина вращающего момента пропорциональна IS, т.е. M ~ IS, где I -ток контуре, S - площадь контура с током, (рис. 1). Векторную величину (1)

называют магнитным моментом контура, который в СИ измеряется в Ам². На пробные контуры с разными р_m, помещаемыми в данную точку магнитного поля, будут действовать разные по величине максимальные вращающие моменты М , но отношение М / р будет для всех контуров одинаково, оно будет являться силовой характеристикой магнитного поля, которая называется магнитной индукцией

В = М /р . (2)

Магнитная индукция есть вектор, направление которого совпадает с направлением нормали контура с током, свободно у становившегося во внешнем магнитном поле(см.рис.2)

Поле вектора В можно представить с помощью силовых линий, (см. рис. 2), как и поле вектора ; таким образом В является аналогом Е .Магнитная индукция в СИ измеряется в теслах: 1 Тл=1 Нм/1 Ам². Тесла равен магнитной индукции однородного поля, в котором на плоский контур с током, который имеет магнитный момент 1 А м², действует максимальный вращающий момент, равный 1 Нм.

На контур с током, помещенный в магнитное поле с индукцией , действует вращающий момент . (3)

Величина его M =

при имеем М = M = p B , при = 0 или = , M= 0.

Динамика материальной точки и твердого тела. Инерциальные си­стемы отсчета. Законы Ньютона. Масса. Импульс. Сила. Силы в механике.

Динамика является основным разделом механики, в ее основе лежат три закона Ньютона, сформулированные им в 1687 г. Законы Ньютона играют исключительную роль в механике и являются (как и все физические законы) обобщением результатов огромного человеческого опыта. Их рассматривают как систему взаимосвязанных законов и опытной проверке подвергают не каждый отдельный закон, а всю систему в целом. Первый закон Ньютона: всякая материальная точка (тело) сохраняет состояние покоя или равномерного прямолинейного движения до тех пор, пока воздействие со стороны других тел не заставит ее изменить это состояние. Стремление тела сохранять состояние покоя или равномерного прямолинейного движения называется инертностью. Поэтому первый закон Ньютона называют также законом инерции. Первый закон Ньютона выполняется не во всякой системе отсчета, а те системы, по отношению к которым он выполняется, называются инерциальными системами отсчета. Инерциальной системой отсчета является такая система отсчета, относительно которой материальная точка, свободная от внешних воздействий, либо покоится, либо движется равномерно и прямолинейно. Первый закон Ньютона утверждает существование инерциальных систем отсчета. Второй закон Ньютона — основной закон динамики поступательного движения — от­вечает на вопрос, как изменяется механическое движение материальной точки (тела) под действием приложенных к ней сил а = kF/m. (6.3)

Соотношение (6.3) выражает второй закон Ньютона: ускорение, приобретаемое материальной точкой (телом), пропорционально вызывающей его силе, совпадает с нею по направлению и обратно пропорционально массе материальной точки (тела). (6.7)

Это выражение — более общая формулировка второго закона Ньютона: скорость изме­нения импульса материальной точки равна действующей на нее силе. Выражение (6.7) называется уравнением движения материальной точки. Взаимодействие между материальными точками (телами) определяется третьим зако­ном Ньютона: всякое действие материальных точек (тел) друг на друга носит характер взаимодействия; силы, с которыми действуют друг на друга материальные точки, всегда равны по модулю, противоположно направлены и действуют вдоль прямой, соединяющей эти точки:

F₁₂ = – F₂₁, (7.1)

где F₁₂ — сила, действующая на первую материальную точку со стороны второй;

F₂₁ — сила, действующая на вторую материальную точку со стороны первой. Эти силы приложены к разным материальным точкам (телам), всегда действуют парами и явля­ются силами одной природы. Масса тела — физическая величина, являющаяся одной из основных характеристик материи, определяющая ее инерционные (инертная масса) и гравитационные (гравитационная масса) свойства. В настоящее время можно считать доказанным, что инертная и гравитационная массы равны друг другу (с точностью, не меньшей 10^–12 их значения). Сила — это векторная величина, являющаяся мерой механического воздействия на тело со стороны других тел или полей, в результате которого тело приобретает ускорение или изменяет свою форму и размеры. Сила трения, которая препятствует скольжению соприкасающихся тел друг относительно друга. Силы трения зависят от относительных скоростей тел. Силы трения могут быть разной природы, но в результате их действия механическая энергия всегда превращается во внутреннюю энергию соприкасающихся тел. На любое тело, расположенное вблизи поверхности Земли, действует сила тяготения F, под влиянием которой и в согласии со вторым законом Ньютона тело начнет двигать­ся с ускорением свободного падения g. Таким образом, в системе отсчета, связанной с Землей, на всякое тело массой т действует сила

называемая силой тяжести. И́мпульс (Количество движения) — векторная физическая величина, являющаяся мерой механического движения тела. В классической механике импульс тела равен произведению массы m этого тела на его скорость v, направление импульса совпадает с направлением вектора скорости: .

ДИСПЕРСИЯ СВЕТА

зависимость преломления показателя n в-ва от частоты n (длины волны l) света или зависимость фазовой скорости световых волн от их частоты. Следствие Д. с.— разложение в спектр пучка белого света при прохождении его сквозь призму (см. СПЕКТРЫ ОПТИЧЕСКИЕ). Изучение этого спектра привело И. Ньютона (1672) к открытию Д. с. Для в-в, прозрачных в данной области спектра, n увеличивается с увеличением v (уменьшением l), чему и соответствует распределение цветов в спектре; такая зависимость n от l наз. нормальной Д. с.

Вблизи полос поглощения в-ва изменение n с изменением l значительно сложнее. Так, для тонкой призмы из р-ра цианина в области поглощения (рис. 1) красные лучи преломляются сильнее фиолетовых, а наименее преломляемым будет зелёный, затем синий (т. н. аномальная Д. с.— уменьшение и с уменьшением l). У всякого в-ва имеются свои полосы поглощения, и общий ход показателя

преломления обусловлен распределением этих полос по спектру. Для наблюдения Д. с. в узких спектр.линиях разработаны спец. методы, основанные на интерференции. На рис. 2 показан вид интерференц. полос в области аномальной дисперсии паров натрия.

Преломление света в в-ве возникает вследствие изменения фазовой скорости света; показатель преломления n=c/cф, где cф—фазовая скорость его в данной среде. По эл.-магн. теории света cф=с/?em, где e— диэлектрич. проницаемость, m — магн. проницаемость. В оптич. области спектра для всех в-в m очень близка к единице. Поэтому n=?e и Д. с. объясняется зависимостью e от частоты. Эта зависимость определяется вз-ствием эл.-магн. поля световой волны с атомами и молекулами, приводящими к поглощению; показатель преломления при этом становится комплексной величиной n^=n+ic, где c — характеризуетпоглощение. В видимой и УФ областях спектра осн. значение имеют колебания эл-нов, а в ИК — колебания ионов.

Согласно классич. представлениям, под действием электрич. поля световой волны эл-ны атомов или молекул совершают вынужденные колебания с частотой, равной частоте приходящей волны. При приближении частоты световой волны к частоте собств. колебаний эл-нов возникает явление резонанса, обусловливающее поглощение света. Наличие собств. частоты колебаний приводит к зависимости n от n, хорошо передающей весь ход Д. с. как вблизи полос поглощения, так и вдали от них. Для того чтобы получить количеств.совпадение с опытом, в классич. теории приходилось вводить для каждой линии поглощения нек-рыеэмпирич. константы («силы осцилляторов»). Согласно электронной теории, справедливы приближённые ф-лы:

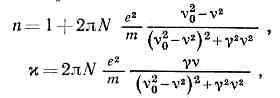
где N — число ч-ц в ед. объёма, m — масса эл-на, g — коэфф. затухания. На рис. 3 приведены графики зависимости n и c от n/n0.

Квант.теория подтвердила качеств. результаты классич. теории и, кроме того, дала возможность связать эти константы с др. хар-ками электронных оболочек атомов (с их волновыми функциями в разных энергетич. состояниях).

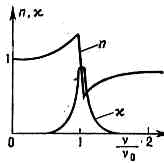
Рис. 3. Графики зависимости n и c от n/n0.

Квант.теория объяснила также особенности Д. с., наблюдающиеся в тех случаях, когда имеется значит. число атомов в возбуждённых состояниях (т. н. отрицательная Д. с.).

Д. с. в прозрачных материалах, применяемых в оптич. приборах, имеет большое значение при расчёте спектральных приборов, при расчёте ахроматич. линз или призм, для уничтожения Д. с., вызывающей хроматическую аберрацию, и др.

Вращательная дисперсия — изменение угла вращения плоскости поляризации j в зависимости от длины волны К. В прозрачных в-вах угол j обычно возрастает с уменьшением К, причём для нек-рых сред приближённо выполняется закон Био: j=К/l2 (К — постоянная для данного в-ва). Вращательная Д. с. такого типа наз. нормальной. В области поглощения света ход вращательной Д. с. значительно сложнее, причём угол j может достигать огромных величин (аномальная вращат. дисперсия). (см. ВРАЩЕНИЕ ПЛОСКОСТИ ПОЛЯРИЗАЦИИ).

Диэлектрики в электрическом поле. Поляризация диэлектриков. Поляризованность. Электрическое смещение. Теорема Гаусса для вектора электрического смещения.

Диэлектрики в электрическом поле и электрики в электрическом поле. В отличие от проводников, в диэлектриках нет свободных зарядов. Все заряды являются связанными : электроны принадлежат своим атомам, а ионы твёрдых диэлектриков колеблются в близи узлов кристаллической решётки.

Соответственно, при помещении диэлектрика в электрическое поле не возникает направленного движения зарядов. Поэтому для диэлектриков не проходят наши доказательства свойств

проводников ведь все эти рассуждения опирались на возможность появления тока. И действительно, ни одно из четырёх свойств проводников, сформулированных в предыдущей статье,

не распростаняется на диэлектрики.

1.Напряжённость электрического поля внутри диэлектрика может быть не равна нулю.

2.Объёмная плотность заряда в диэлектрике может быть отличной от нуля.

3.Линии напряжённости могут быть не перпендикулярны поверхности диэлектрика.

4.Различные точки диэлектрика могут иметь разный потенциал. Стало быть, говорить о

¾потенциале диэлектрика¿ не приходится.

Д иэлектрик, помещенный во внешнее электрическое поле, поляризуется под действием этого поля. Поляризацией диэлектрика называется процесс приобретения им отличного от нуля макроскопического дипольного момента. Степень поляризации диэлектрика характеризуется векторной величиной, которая называется поляризованостью или вектором поляризации (P). Поляризованность определяется как электрический момент единицы объема диэлектрика где N - число молекул в объеме . Поляризованность P часто называют поляризацией, понимая под этим количественную меру этого процесса. В диэлектриках различают следующие типы поляризации: электронную, ориентационную и решеточную (для ионных кристаллов). Электронный тип поляризации характерен для диэлектриков с неполярными молекулами. Во внешнем электрическом поле (рис. 2.1) положительные заряды внутри молекулы смещаются по направлению поля, а отрицательные в противоположном направлении, в результате чего молекулы приобретают дипольный момент, направленный вдоль внешнего поля

Индуцированный дипольный момент молекулы пропорционален напряженности внешнего электрического поля , где - поляризуемость молекулы. Значение поляризованности в этом случае равно , где n - концентрация молекул ; - индуцированный дипольный момент молекулы, который одинаков для всех молекул и направление которого совпадает с направлением внешнего поля. Ориентационнный тип поляризации характерен для полярных диэлектриков. В отсутствие внешнего электрического поля молекулярные диполи ориентированы случайным образом, так что макроскопический электрический момент диэлектрика равен нулю.

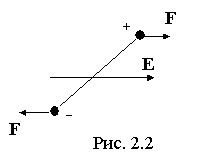
Если поместить такой диэлектрик во внешнее электрическое поле, то на молекулу-диполь будет действовать момент сил (рис. 2.2), стремящийся ориентировать ее дипольный момент в направлении напряженности поля. Однако полной ориентации не происходит, поскольку тепловое движение стремится разрушить действие внешнего электрического поля.

Такая поляризация называется ориентационной. Поляризованность в этом случае равна , где <p> - среднее значение составляющей дипольного момента молекулы в направлении внешнего поля. Решеточный тип поляризации характерен для ионных кристаллов. В ионных кристаллах (NaCl и т.д.) в отсутствие внешнего поля дипольный момент каждой элементарной ячейки равен нулю (рис. 2.3.а), под влиянием внешнего электрического поля положительные и отрицательные ионы смещаются в противоположные стороны (рис. 2.3.б). Каждая ячейка кристалла становится диполем, кристалл поляризуется. Такая поляризация называется решеточной. Поляризованность и в этом случае можно определить как , где - значение дипольного момента элементарной ячейки, n - число ячеек в единице объема.

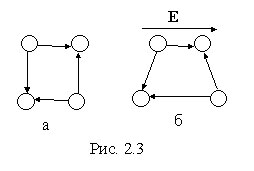
Поляризованность изотропных диэлектриков любого типа связана с напряженностью поля соотношением , где - диэлектрическая восприимчивость диэлектрика.

Электрическое поле в диэлектрической среде создается как свободными, так и связанными зарядами, так что вектор напряженности E, характеризующий результирующее поле в диэлектрике,

. Если обозначить объемную плотность свободных зарядов , а связанных зарядов , то присутствие связанных зарядов отразится в теореме Гаусса следующим образом:

,

в дифференциальной форме, либо в интегральной форме

.

С учетом выражения (2.1)

,

откуда для вектора электрического смещения (индукции) находим

.

Последнее выражение показывает, что вектор электрической индукции учитывает поляризованность среды. Возвращаясь к соответствующим формулировкам теоремы Гаусса

; ,

можно видеть, что вектор электрического смещения характеризует источники электрического поля, т. е. свободные заряды, на которых этот вектор начинается и заканчивается. Так как , то . Напряженность электрического поля характеризует как свободные, так и связанные заряды, поэтому вектор напряженности терпит разрывы на границах областей, где присутствуют связанные заряды, например на границе раздела двух диэлектриков с различными .

Законы сохранения в механике: закон сохранения импульса, закон сохранения момента им­пульса, закон сохранения энергии в механике. Законы сохранения как след­ствие симметрии пространства и времени. (13.3)

т. е. полная механическая энергия системы сохраняется постоянной. Выражение (13.3) представляет собой закон сохранение механической энергии: в системе тел, между которыми действуют только консервативные силы, полная механическая энергия со­храняется, т. е. не изменяется со временем.Т-кинетиская энергия , П- потенциальня энргия.

Последнее выражение и является законом сохранения импульса: импульс замкнутой системы сохраняется, т. е. не изменяется с течением времени.

Закон сохранения импульса справедлив не только в классической физике, хотя он и получен как следствие законов Ньютона. Эксперименты доказывают, что он выпол­няется и для замкнутых систем микрочастиц (они подчиняются законам квантовой механики). Этот закон носит универсальный характер, т. е. закон сохранения импуль­са — фундаментальный закон природы. (19.4)

Выражение (19.4) представляет собой закон сохранения момента импульса: момент импульса замкнутой системы сохраняется, т. е. не изменяется с течением времени.

Закон сохранения момента импульса — фундаментальный закон природы. Он связан со свойством симметрии пространства — его изотропностью, т. е. с инвариантностью физических законов относительно выбора направления осей координат системы от­счета (относительно поворота замкнутой системы в пространстве на любой угол).

Магнитное поле в веществе. Магнетики. Виды магнетиков. Намагниченность.

Подобно тому, как для количественного описания поляризации диэлектриков вводи­лась поляризованность , для количественного описания намагничения магнетиков вводят векторную величину — намагниченность, определяемую магнитным моментом единицы объема магнетика:

где — магнитный момент магнетика, представляющий собой векторную сумму магнитных моментов отдельных молекул.

Закон полного тока для магнитного поля в веществе (теорема о циркуляции вектора В) является обобщением закона (118.1):

где I и I' — соответственно алгебраические суммы макротоков (токов проводимости) и микротоков (молекулярных токов), охватываемых произвольным замкнутым кон­туром L. Таким образом, циркуляция вектора магнитной индукции В по произволь­ному замкнутому контуру равна алгебраической сумме токов проводимости и молеку­лярных токов, охватываемых этим контуром, умноженной на магнитную постоянную.

Всякое вещество является магнетиком, т. е. оно способно под действием магнитного поля приобретать магнитный момент (намагничиваться).

Наведенные составляющие магнитных полей атомов (молекул) складываются и образуют собственное магнитное поле вещества, ослабляющее внешнее магнитное поле. Этот эффект получил название диамагнитного эффекта, а вещества, намагничивающиеся во внешнем

магнитном поле против направления поля, называются диамагнетиками.

В отсутствие внешнего магнитного поля диамагнетик немагнитен, поскольку в дан­ном случае магнитные моменты электронов взаимно компенсируются, и суммарный магнитный момент атома (он равен векторной сумме магнитных моментов (орбиталь­ных и спиновых) составляющих атом электронов) равен нулю. Так как диамагнитный эффект обусловлен действием внешнего магнитного поля на электроны атомов вещества, то диамагнетизм свойствен всем веществам. Однако наряду с диамагнитными веществами существуют и парамагнитные — вещества, нама­гничивающиеся во внешнем магнитном поле по направлению поля. Парамагнетик намагничивается, создавая собственное маг­нитное поле, совпадающее по направлению с внешним полем и усиливающее его. Этот эффект называется парамагнитным. При ослаблении внешнего магнитного поля да нуля ориентация магнитных моментов вследствие теплового движения нарушается и парамагнетик размагничивается.

Помимо рассмотренных двух классов веществ — диа- и парамагнетиков, называемых слабомагнитными веществами, существуют еще сильномагнитные вещества — ферромагнетики — вещества, обладающие спонтанной намагниченностью, т. е. они намагниче­ны даже при отсутствии внешнего магнитного поля. К ферромагнетикам кроме основ­ного их представителя — железа (от него и идет название «ферромагнетизм») — от­носятся, например, кобальт, никель, гадолиний, их сплавы и соединения.

Ферромагнетики помимо способности сильно намагничиваться обладают еще и другими свойствами, существенно отличающими их от диа- и парамагнетиков. Если для слабомагнитных веществ зависимость J от Н линейна , то для ферромагнетиков эта зависимость, впервые изученная в 1878 г. методом баллистичес­кого гальванометра для железа русским физиком А.Г. Столетовым (1839—1896), является довольно сложной. По мере возрастания Н намагниченность J сначала растет быстро, затем медленнее и, наконец, достигается так называемое магнитное насыщение J_нас, уже не зависящее от напряженности поля. Характерная особенность ферромагнетиков состоит также в том, что для них зависимость J от H (а следовательно, и В от Н) определяется предысторией намагниче­ния ферромагнетика. Это явление получило название магнитного гистерезиса. вВферромагнетике наблюдается остаточное намагничение J_ос

Магнитный поток. Теорема Гаусса для магнитного поля. Работа по перемещению проводника с током в магнитном поле.

Потоком вектора магнитной индукции (магнитным потоком) через площадку dS называ­ется скалярная физическая величина, равная

(120.1)

где B_n=В cos  —проекция вектора В на направление нормали к площадке dS ( — угол между векторами n и В), dS=dSn — вектор, модуль которого равен dS, а направление его совпадает с направлением нормали n к площадке. Поток вектора В может быть как положительным, так и отрицательным в зависимости от знака cos  (определяется выбором положительного направления нормали n). Поток вектора В связывают с контуром, по которому течет ток. В таком случае положительное направление нормали к контуру нами уже определено: оно связывается с током правилом правого винта. Таким образом, магнитный поток, создаваемый контуром через поверхность, ограниченную им самим, всегда положителен.

Поток вектора магнитной индукции Ф_B через произвольную поверхность S равен

(120.2)

Для однородного поля и плоской поверхности, расположенной перпендикулярно вектору В, B_n=B=const и

Из этой формулы определяется единица магнитного потока вебер (Вб): 1 Вб — маг­нитный поток, проходящий сквозь плоскую поверхность площадью 1 м², расположен­ную перпендикулярно однородному магнитному полю, индукция которого равна 1 Тл (1 Вб=1 Тлм²).

Теорема Гаусса для поля В: поток вектора магнитной индукции сквозь любую замкнутую поверхность равен нулю:

(120.3)

Эта теорема отражает факт отсутствия магнитных зарядов, вследствие чего линии магнитной индукции не имеют ни начала, ни конца и являются замкнутыми. (121.1)

т. е. работа по перемещению проводника с током в магнитном поле равна произведе­нию силы тока на магнитный поток, пересеченный движущимся проводником. Получен­ная формула справедлива и для произвольного направления вектора В.

Работа dA, совершаемая силами Ампера при рассматриваемом перемещении кон­тура в магнитном поле, равна алгебраической сумме работ по перемещению провод­ников AВС (dA₁) и CDA (dA₂), т. е.

МАГНИТНОЕ ПОЛЕ ПРЯМОЛИНЕЙНОГО ТОКА

dl=r dα/sinα; r = R/sinα; dB=μ0 μ I r dα sinα sin(c.2)α /

/ 4π sinα R(c.2) = μ0 μ I sinα dα / 4πR; B=(μ0 μ I / 4πR)*∫[0 - π] sinαdα=μ0 μ I / 2πR;

Второй случай: Магнитное поле в центре кругового тока

dB=μ0 μ I dl / 4πR(c.2); B=(μ0 μ I / 4πR(c.2))*∫[0 — 2πR] dl = = μ0 μ I / 2R;

ЗАКОН ПОЛНОГО ТОКА (ЦИРКУЛЯЦИЯ ВЕКТОРА МАГ. ПОЛЯ)

Замкнутый ∫[по L] B(в) dl(в); Для того, чтобы определить циркуляцию вектора рассмотрим прямолинейный проводник с током.

Выберем контур l в виде окружности, в центре которой

находится проводник с током. Замкнутый ∫B(в)dl(в)= =B*замкнутый ∫[по L]dl=μ0 μ I 2 π R / 2 πR=μ0μ I;

Эта формула справедлива для контура L любой формы, охватывающего проводник с током. Из этой формулы можно сделать 2 вывода:

1)магнитное поле прямлинейного тока является вихревым — циркуляция вектора B вдоль линии магнитной индукции. 2)циркуляция вектора B магнитного поля прямого тока в вакууме (μ=1) одинаково вдоль всех линий магнитной индукции и равна μ0*I.

Рассмотрим контур, неохватывающий проводник с током. Найдем циркуляцию вектора В по этому контуру: Замкнутый ∫[по L] B(в)dl(в); B(в)dl(в)=Bdlcosα

dlcosα=rdφ; Замкнутый ∫[по L] B(в)dl(в)=

=∫[по 1-a-2]B(в)dl(в) + ∫[2-b -1] B(в) dl;

B=μ0 I/2πr ; B(в)dl=Br dφ=μ0 I r dφ / 2πr = μ0 I dφ/2π;

(μ0 I/ 2π)*(∫[по 1-a-2] dφ + ∫[2-b-1] dφ)=(μ0 I / 2π)*(∫[φ1 — φ2]dφ + ∫[φ2 — φ1]dφ)=0; Замкнутый ∫B(в)dl(в)=0; Циркуляция вектора B по замкнутому контуру неохватывающая проводник с током равна нулю. Замкнутый ∫[по L] B(в) dl(в)=μ0 Σji=μ0 Jохв; Циркляция вектора В вдоль произвольного замкнутого контура равна произведению магнитной постоянной на алгебраическую сумму токов, охватываемых этим контуром, т.е. на электрический ток через поверхность S, натянутую на этот контур

Замкнутый ∫[по L] B(в)dl(в)=μ0 ∫[по S] jdS(в)

МАГНИТНЫЙ ПОТОК. ТЕОРЕМА ГАУССА ДЛЯ МАГ. ПОЛЯ

dФm=B(в)dS(в); Фm=∫[по S]B(в)dS(в); Линии индукции магнитного поля замкнуты. Рассмотрим замкнутую повехность S и линию индукции, пронизывающую эту поверхность. Т.к. линия индукции замкнута,

то каждая из них будет пронизываться замкнутой поверхностью дважды, один раз входя, другой раз выходя. В результате этого она войдет в выражение для потока вектора В через замкнутую поверхность дважды с противоположными знаками. В результате этого суммарный поток вектора магнитной индукции через замкнутую поверхность будет равен нулю, поэтому теорема гаусса для магнитного поля имеет вид:

Замкнутый ∫[по S] dS(в)=0; Эта формула отражает тот факт, что в природе не существует магнитных зарядов, т.е. источника, на котором могли бы начинаться и заканчиваться линии индукции магнитного поля. Магнитный поток через поверхность, ограниченную замкнутым контуром, называется потоком сцепления этого контура ψ. Например потокосцепление рамки и катушки из N витков: ψ=NФ; Ф — магнитный поток через каждый виток.

Потокосцепление контура обусловлена магнитном полем тка в самом контуре называется потокосцеплением самоиндукции. Потокосцепление контура, обусловленное магнитным полем тока в другом контуре, называется потокосцеплением взаимоиндукции.

РАБОТА ПЕРЕМЕЩЕНИЯ ПРОВОДНИКА С ТОКОМ В МАГНИТНОМ ПОЛЕ

На проводник с током в магнитном поле действует сила ампера. Если проводник не прикреплен, то под действием этой силы ток будет перемещаться и совершает работу.Вычислим ее: Fa=IBl; dA=Fa dx=IBldx=IBdS; dS=ldx; dS=ldx;

BdS=dФm; dA=IdФm; A12=∫[1 - 2] IdФm; Если при перемещении проводника y=const, то A12=J(Ф2 — Ф1). Работа по перемещению проводника с током в магнитном поле равна произведению силы тока на магнитный поток, пересеченный движущимся проводником.

Механическое движение. Система отсчета. Понятие материальной точ­ки. Основные понятия кинематики поступательного и вращательного движения.

Механическое движе­ние — это изменение с течением времени взаимного расположения тел или их частей. Механика для описания движения тел в зависимости от условий конкретных задач использует разные физические модели. Простейшей моделью является материальная точка — тело, обладающее массой, размерами которого в данной задаче можно пренебречь. Понятие материальной точки — абстрактное, но его введение облегчает решение практических задач. Например, изучая движение планет по орбитам вокруг Солнца, можно принять их за материальные точки. Любое движение твердого тела можно представить как комбинацию поступатель­ного и вращательного движений. Поступательное движение — это движение, при кото­ром любая прямая, жестко связанная с движущимся телом, остается параллельной своему первоначальному положению. Вращательное движение — это движение, при котором все точки тела движутся по окружностям, центры которых лежат на одной и той же прямой, называемой осью вращения.Движение тел происходит в пространстве и во времени. Поэтому для описания движения материальной точки надо знать, в каких местах пространства эта точка находилась и в какие моменты времени она проходила то или иное положение.Положение материальной точки определяется по отношению к какому-либо друго­му, произвольно выбранному телу, называемому телом отсчета. С ним связывается система отсчета — совокупность системы координат и часов, связанных с телом от­счета. При движении материальной точки ее координаты с течением времени изменяются. В общем случае ее движение определяется скалярными уравнениями

x = x(t), у = y(t), z = z(t), (1.1)

эквивалентными векторному уравнению

r = r(t). (1.2)

Уравнения (1.1) и соответственно (1.2) называются кинематическими уравнениями дви­жения материальной точки.

Ос­новы молекулярно-кинетической теории. Термодинамические параметры. Равновесные состо­яния и процессы.

Современная молекулярно-кинетическая теория строения вещества – теория, в основе которой лежат три положения, подтвержденные экспериментально и теоретически: все тела состоят из мельчайших частиц – атомов или молекул; атомы и молекулы вещества всегда находятся в непрерывном хаотическом движении; между частицами любого вещества существуют силы взаимодействия. Огромная роль молекулярно-кинетической теории в развитии физики состоит в том, что она позволила с единых позиций подойти к изучению физических явлений, так или иначе связанных с характером движения молекул в телах. Многие свойства тел в разных агрегатных состояниях объясняются различиями в характере движения атомов и молекул в газах, жидкостях и твердых телах. В свою очередь, особенности теплового движения в трех агрегатных состояниях связаны с тем, что между молекулами действуют силы взаимного притяжения и отталкивания. Чем меньше среднее расстояние между молекулами, тем в большей степени проявляют себя эти силы. Кинетическая теория газов основана на следующих общих положениях классической статистической физики:

а) в системе частиц выполняются законы сохранения импульса, момента импульса, энергии, электрического заряда (для систем заряженных частиц) и числа частиц (для закрытых систем частиц, не претерпевающих химических и других превращений);

б) все частицы системы считаются “мечеными”, т. е. предполагается возможность отличать друг от друга тождественные частицы (например, молекулы одного и того же вещества);

в) все физические процессы в системе протекают в пространстве и времени непрерывно (например, энергия молекулы может изменяться под влиянием внешних воздействий на любую величину, т. е. непрерывно);

г) каждая частица системы может иметь совершенно произвольные значения координат (в пределах объема системы) и компонент скорости совершенно независимо от того, каковы значения этих характеристик у других частиц системы.

Термодинамическая система – совокупность макроскопических тел, которые могут взаимодействовать между собой и с другими телами (внешней средой) – обмениваться с ними энергией и веществом. Обмен энергией и веществом может происходить как внутри самой системы между ее частями, так и между системой и внешней средой. В зависимости от возможных способов изоляции системы от внешней среды различают несколько видов термодинамических систем. Термодинамическими параметрами (параметрами состояния) называются физические величины, служащие для характеристики состояния термодинамической системы.Примерами термодинамических параметров являются давление, объем, температура, концентрация. Различают два типа термодинамических параметров: экстенсивные и интенсивные. Первые пропорциональны количеству вещества в данной термодинамической системе, вторые не зависят от количества вещества в системе. Простейшим экстенсивным параметром является объем V системы. Величину v, равную отношению объема системы к ее массе, называют удельным объемом системы. Простейшими интенсивными параметрами являются давление р и температура Т. Равновесное состояние термодинамической системы – состояние системы, при котором все параметры имеют определенные значения, и в котором система может оставаться сколько угодно долго. Температура во всех частях термодинамической системы, находящейся в равновесном состоянии, одинакова. Под термодинамическим процессом понимают всякое изменение состояния рассматриваемой термодинамической системы, характеризующееся изменением ее термодинамических параметров. Термодинамический процесс называется равновесным, если в этом процессе система проходит непрерывный ряд бесконечно близких термодинамически равновесных состояний Примерами простейших термодинамических процессов могут служить следующие процессы:

а) изотермический процесс, при котором температура системы не изменяется (T = const);

б) изохорный процесс, происходящий при постоянном объеме системы (V = const);

в) изобарный процесс, происходящий при постоянном давлении в системе (p = const);

г) адиабатный процесс, происходящий без теплообмена между системой и внешней средой.

Первое начало термодинамики. Изопроцессы.

U = Q - A, или Q =U + A. (3.4)

Уравнение (3.4) выражает первое начало термодинамики – теплота, сообщенная системе, идет на приращение внутренней энергии и совершение системой работы над внешними телами. Выражение (3.4) в дифференциальной форме будет иметь вид

Q = dU +A, (3.5)

где dU — бесконечно малое изменение внутренней энергии системы, A — элементарная работа, — бесконечно малое количество теплоты. В этом выражении dU является полным дифференциалом, a A и Q таковыми не являются. В дальнейшем будем использовать запись первого начала термодинамики в форме (3.5).Из формулы (3.4) следует, что в СИ количество теплоты выражается в тех же единицах, что работа и энергия, т. е. в джоулях (Дж). Изохорный процесс (V = const). Диаграмма этого процесса (изохора) в координатах p,V изображается прямой, параллельной оси ординат (рис. 13), где процесс 1—2 есть изохорное нагревание, а 1—3 — изохорное охлаждение. При изохорном процессе газ не совершает работы над внешними телами, т. е. A = pdV = 0.Из первого начала термодинамики (Q = dU +A) для изохорного процесса следует, что вся теплота, сообщаемая газу, идет на увеличение его внутренней энергии: Q = dU. Согласно формуле (3.9), dU_m = C_VdT.Тогда для произвольной массы газа получим

Изобарный процесс (p = const). Диаграмма этого процесса (изобара) в координатах р,V изображается прямой, параллельной оси V. При изобарном процессе работа газа (см. формулу 3.3) при увеличении объема от V₁ до V₂ равна

(3.15)

Рисунок 13 - Изохора Рисунок 14 - Изобара

и определяется площадью заштрихованного прямоугольника (рис. 14). Если использовать уравнение (1.12) Клапейрона - Менделеева для выбранных нами двух состояний, то

, ,

откуда

.Тогда, выражение (3.15) для работы изобарного расширения примет вид

В изобарном процессе при сообщении газу массой m количества теплоты

его внутренняя энергия возрастает на величину (согласно формуле 3.9)

.