Тривалість роботи
Вхідний контроль, виконання лабораторної роботи, формування отриманих результатів у формі письмового звіту згідно завдання, аналіз результатів роботи та висновки, захист роботи виконуються протягом двох аудиторних занять.
Основні теоретичні положення
Розташуємо масив зверху вниз, від нульового елементу - до останнього.
Ідея методу: крок сортування полягає в проході від низу до верху по масиву. По дорозі є видимими пари сусідніх елементів. Якщо елементи деякої пари знаходяться в неправильному порядку, то міняємо їх місцями.
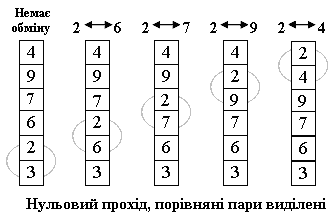
Після нульового проходу по масиву "вгорі" виявляється "найлегший" елемент - звідси аналогія з бульбашкою. Наступний прохід робиться до другого зверху елементу, таким чином другий за величиною елемент піднімається на правильну позицію...
Робимо проходи по нижній частині масиву, що все зменшується, до тих пір, поки в ній не залишиться тільки один елемент. На цьому сортування закінчується, оскільки послідовність впорядкована за збільшенням.
template<class T>
void bubbleSort(T a[], long size){
long i, j;
T x;
for( i=0; i < size; i++){ // i - номер проходу
for( j = size-1; j > i; j-- ){ // внутрішній цикл проходу
if ( а[j-1]> а[j]) {
x=a[j-1]; а[j-1]=a[j]; а[j]=x;
}
}
}
}
Середнє число порівнянь і обмінів мають квадратичний порядок зростання: Theta(n2), звідси і слідує, що алгоритм бульбашки дуже повільний і малоефективний.
Проте, у нього є величезний плюс: він простий і його можна по-всякому покращувати. Чим ми зараз і займемося.
По-перше, розглянемо ситуацію, коли на якому-небудь з проходів не відбулося жодного обміну. Що це означає ?
Це означає, що всі пари розташовані в правильному порядку, так що масив вже відсортований. І продовжувати процес не має сенсу(особливо, якщо масив був відсортований із самого початку !).
Отже, перше поліпшення алгоритму полягає в запам'ятовуванні, чи проводився на даному проході який-небудь обмін. Якщо немає - алгоритм закінчує роботу.
Процес поліпшення можна продовжити, якщо запам'ятовувати не тільки сам факт обміну, але і індекс останнього обміну. Дійсно: всі пари сусідніх елементів з індексами, меншими до, вже розташовані в потрібному порядку. Подальші проходи можна закінчувати на індексі до, замість того щоб рухатися до встановленої заздалегідь верхньої межі i.
Інше покращення алгоритму можна отримати з наступного спостереження. Хоча легка бульбашка знизу підніметься вгору за один прохід, важкі бульбашки опускаються з мінімальною швидкістю: один крок за ітерацію. Отже масив 2 3 4 5 6 1 буде відсортований за 1 прохід, а сортування послідовності 6 1 2 3 4 5 вимагає 5 проходів.
Щоб уникнути подібного ефекту, можна міняти напрям наступних один за іншим проходів. Алгоритм, що вийшов, іноді називають "шейкер-сортування".
template<class T>
void shakerSort(T a[], long size){
long j, до = size-1;
long lb=1, ub = size-1; // межі невідсортованої частини масиву
T x;
do {
// прохід від низу до верху
for( j=ub; j>0; j-- ){
if ( а[j-1]> а[j]) {
x=a[j-1]; а[j-1]=a[j]; а[j]=x;
k=j;
}
}
lb = k+1;
// прохід зверху вниз
for (j=1; j<=ub; j++) {
if ( а[j-1]> а[j]) {
x=a[j-1]; а[j-1]=a[j]; а[j]=x;
k=j;
}
}
ub = k-1;
} while ( lb < ub );
}
Наскільки описані зміни вплинули на ефективність методу ? Середня кількість порівнянь, хоч і зменшилося, але залишається O(n2), тоді як число обмінів не помінялося взагалі ніяк. Середня(воно ж гірше) кількість операцій залишається квадратичною.
Додаткова пам'ять, очевидно, не потрібна. Поведінка вдосконаленого (але не початкового) методу задоволена природне, майже відсортований масив буде відсортований набагато швидше випадкового. Сортування бульбашкою стійке, проте шейкер-сортування втрачає цю якість.
На практиці метод бульбашки, навіть з поліпшеннями, працює, на жаль, дуже поволі. А тому - майже не застосовується.