Решение:

Условие задачи не дописано – отсутствует значение потенциала φ на расстоянии r от точечного заряда.

По определению, вектор напряженности электрического поля:

где φ – потенциал;

единичные векторы.

Поскольку в случае точечного заряда силовые линии направлены радиально от точечного заряда, (52) можно переписать так:

где r – расстояние от заряда до исследуемой точки.

Поскольку заряд положителен, то силовые линии поля направлены радиально от него, а, следовательно, градиент потенциала gradφ направлен противоположно, то есть – к заряду.

Численное значение градиента потенциала:

Поскольку условие задачи не дописано, примем численное значение потенциала равным φ = 1 В.

Тогда искомый градиент потенциала:

Ответ: поскольку условие задачи не дописано, принято численное значение потенциала φ = 1 В, при таком потенциале, его градиент в исследуемой точке равен gradφ = 10 B/м; поскольку точечный заряд положителен, то градиент потенциала направлен радиально к заряду.

12.

Какова разность потенциалов между двумя точками электростатического поля, если при перемещении между ними заряда q = 0,012 Кл, полем была совершена работа А = 0,36 Дж?

Дано:

q = 0,012 Кл

А = 0,36 Дж

Найти:

U - ?

Решение:

По определению, работа А электрического поля по перемещению заряда q между точками с разностью потенциалов U, равна:

Отсюда искомая разность потенциалов:

Вычисляем:

Ответ: U = 30 B.

13.

Пространство между пластинами плоского конденсатора заполнено стеклом (ε = 7). Расстояние между пластинами d = 5 мм, разность потенциалов U=1кВ. Определить: 1) напряженность поля в стекле; 2) поверхностную плотность заряда на пластинах конденсатора.

Дано:

ε = 7

d = 5 мм = 0,005 м

U=1кВ = 1000 В

Найти:

E, σ - ?

Решение:

Напряженность электрического поля между пластинами конденсатора:

где U – напряжение между пластинами;

d – расстояние между пластинами;

Вычисляем:

Электроемкость плоского конденсатора:

где ε₀ = 8,85∙10^-12 Ф/м – электрическая постоянная;

ε – диэлектрическая проницаемость среды между пластинами;

S – площадь пластины.

Тогда заряд конденсатора:

Искомая поверхностная плотность заряда:

Вычисляем:

Ответ: E = 2∙10⁵ В/м; σ = 1,24∙10^-5 Кл/м².

14.

Напряженность электрического поля у поверхности Земли равна в среднем Е=130 В/м. Определить заряд Земли, допустив, что она имеет форму шара радиус 6400 км.

Дано:

Е=130 В/м

R = 6400 км = 6,4∙10⁶ м

Найти:

q - ?

Решение:

Полагая, что Земля имеет форму шара, можем записать формулу напряженности электрического поля на ее поверхности:

где q – заряд Земли;

ε = 1 – диэлектрическая проницаемость среды, в которой находится заряженный шар (в нашем случае это воздух с диэлектрической проницаемостью равной единице);

ε₀ = 8,85∙10^-12 Ф/м – электрическая постоянная;

R – радиус Земли.

Тогда искомый заряд Земли:

Вычисляем:

Ответ: q = 5,92∙10⁵ Кл.

15.

В однородное магнитное поле с индукцией 0,1 Тл помещена квадратная рамка площадью 25 см². Нормаль к плоскости рамки составляет с направлением магнитного поля угол 60°. Определить вращающий момент, действующий на рамку, если по ней течет ток I = 1 A.

Дано:

B = 0,1 Тл

S = 25 см² = 25∙10^-4 м²

α = 60°

I = 1 A

Найти:

M - ?

Решение:

Заданная в условии ситуация приведена на рисунке 7.

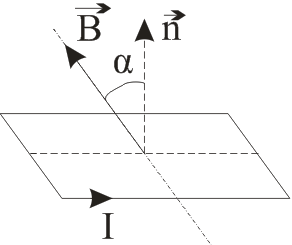
Рисунок 7

B – магнитная индукция поля, в котором находится рамка с током I.

Угол между силовыми линиями поля и нормалью к рамке равен α.

Тогда искомый вращающий момент, действующий на рамку:

где p – магнитный момент рамки с током, равный:

где S – площадь рамки.

Тогда (68) примет вид:

Вычисляем:

Ответ: М = 2,17∙10^-4 Н∙м.

16.

Электрон вращается по круговой орбите вокруг протона. Найти силу их электрического взаимодействия, если средний радиус орбиты электрона равен 10^-8 см. e = 1,6∙10^-19 Кл.

Дано:

R = 10^-8 см = 10^-10 м

e = 1,6∙10^-19 Кл

Найти:

F - ?