1.

Два маленьких шарика q₁ = 4 нКл и q₂ = 2 нКл находятся на расстоянии 60 см друг от друга. Определить напряженность Е электрического поля в точке, лежащей посередине между ними.

Дано:

q₁ = 4 нКл = 4∙10^-9 Кл

q₂ = 2 нКл = 2∙10^-9 Кл

d = 60 см = 0,6 м

Найти:

E - ?

Решение:

Заданная в условии ситуация приведена на рисунке 1.

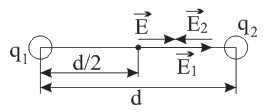
Рисунок 1

На расстоянии d друг от друга расположены заряды q₁ и q₂. В точке, лежащей на середине отрезка d, заряд q₁ создает электрическое поле Е₁, а заряд q₂ – поле Е₂ (направление линий напряженности – от положительных зарядов к отрицательным).

Результирующая напряженность электрического поля в исследуемой точке:

В скалярной форме:

Напряженности полей Е₁ и Е₂ найдем как для точечных зарядов, поскольку размеры шариков пренебрежимо малы по сравнению с расстоянием между ними:

где ε = 1 – диэлектрическая проницаемость среды (в нашем случае воздух, раз не сказано иного);

ε₀ = 8,85∙10^-12 Ф/м – электрическая постоянная.

Тогда (2) примет вид:

Вычисляем:

Ответ: E = 200 В/м.

2.

Точечный +q находится в центре сферической поверхности. Если увеличить ее радиус, то поток вектора через поверхность сферы: a) не изменится; б) увеличится; в) уменьшится.

Решение:

Во всех точках поверхности сферы радиусом R вектор напряженности E электрического поля направлен вдоль нормали к поверхности сферы (поэтому угол между ними равен нулю), его модуль постоянен и по закону Кулона равен:

где q – заряд, находящийся в центре сферы;

ε = 1 – диэлектрическая проницаемость среды (в нашем случае воздух, раз не сказано иного);

ε₀ = 8,85∙10^-12 Ф/м – электрическая постоянная.

Выделим на поверхности сферы малую площадку площадью ΔS_i, поток вектора напряженности через эту площадку равен:

Так как модуль вектора напряженности во всех точках сферы одинаков, суммирование потоков через поверхность сферы, сводится к суммированию площадей участков, на которые разбивается сфера. Вычислим поток вектора напряженности:

где площадь поверхности сферы. Как видим, поток вектора напряженности электрического поля сквозь сферу не зависит от радиуса сферы, поэтому при увеличении радиуса сферы, поток вектора напряженности сквозь нее не изменится.

Ответ: a) не изменится.

3.

Плотность электрического тока в медном проводе равна 10 А/см². Определить удельную тепловую мощность тока, если удельное сопротивление меди равно 17 нОм∙м.

Дано:

j = 10 A/см² = 10⁵ А/м²

ρ = 17 нОм∙м = 17∙10^-9 Ом∙м

Найти:

p - ?

Решение:

Мощность тока I, проходящего по проводнику с сопротивлением R:

С другой стороны, сила тока равна:

где j – плотность тока;

S – площадь поперечного сечения проводника.

Сопротивление проводника:

где ρ – удельное сопротивление проводника;

L – длина проводника.

Подставив (11) и (12) в (10), получим:

где V – объем проводника.

Тогда искомая удельная мощность тока:

Ответ: p = 170 Вт/м³.

4.

Какое количество теплоты выделится в проводнике сопротивлением 100 Ом за 30 с, если сила тока i в нем равномерно убывает от I₀ = 10 A до I = 0?

Дано:

R = 100 Ом

T = 30 c

I₀ = 10 A

I = 0

Найти:

Q - ?

Решение:

Запишем закон Джоуля-Ленца:

где Q – количество теплоты, выделившееся в проводнике сопротивлением R за время t при токе i.

Поскольку ток линейно изменяется от I₀ до I, то закон изменения тока можно представить в виде:

где k – коэффициент пропорциональности, равный:

где Т – время действия тока. Тогда (15) примет вид:

Ответ: Q = 10⁵ Дж.

5.

Электродвижущая сила батареи равна 20 В. Коэффициент полезного действия при силе тока 4 А равен 0,8. Чему равно внутреннее сопротивление батареи?

Дано:

E = 20 B

I = 4 A

η = 0,8

Найти:

r - ?

Решение:

На рисунке 2 приведена схема рассматриваемой цепи.

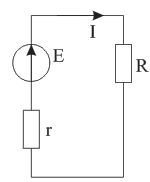
Рисунок 2

Полезная мощность:

где I – ток в цепи;

R – внешнее сопротивление цепи.

Мощность источника:

где E – ЭДС источника.

Тогда КПД:

Отсюда:

По закону Ома:

где r – внутреннее сопротивление источника ЭДС.

Подставим (22) в (23) и выразим r:

Вычисляем:

Ответ: r = 1 Ом.

6.

Плотность тока в проводнике длиной 25 м и удельным сопротивлением 42∙10^-8 Ом∙м равна 4 МА/м². Определить разность потенциалов на концах проводника.

Дано:

L = 25 м

ρ = 42∙10^-8 Ом∙м

j = 4 МА/м² = 4∙10⁶ А/м²

Найти:

U - ?

Решение:

По закону Ома, напряжение на проводнике сопротивлением R с током I равно:

Сила тока:

где j – плотность тока;

S – площадь поперечного сечения проводника.

Сопротивление проводника:

где ρ – удельное сопротивление проводника;

L – длина проводника.

Подставим (27) и (28) в (26):

Ответ: U = 42 B.

7.

На рисунке 3 представлена зависимость магнитного потока, пронизывающего некоторый замкнутый контур, от времени. На каком интервале времени ЭДС индукции максимальна? Минимальна?

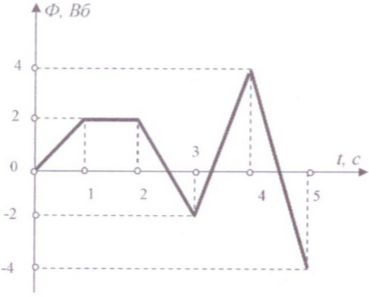
Рисунок 3

Решение:

По закону Фарадея-Ленца, ЭДС индукции равна:

где Ф – магнитный поток;

t – время.

Поскольку нас интересует абсолютная величина ЭДС индукции, знак “минус”, определяющий лишь направление этой ЭДС, можно отбросить:

На всех временных диапазонах, кроме 1-2, магнитный поток изменяется линейно:

где k – некоторый постоянный для каждого диапазона коэффициент.

На участке 1-2 магнитный поток не изменяется, следовательно, согласно (30), ЭДС индукции на этом временном интервале равна нулю, а значит, минимальна.

Рассматриваем остальные диапазоны времени.

На остальных участках, поскольку магнитный поток изменяется линейно, выражение (31) можно переписать так:

С другой стороны, коэффициент k есть ни что иное как:

Таким образом, подставив (34) в (33), получим:

Коэффициент k на каждом диапазоне имеет разный знак, следовательно, ЭДС индукции на этих временных промежутках имеет разное направление, однако, поскольку нас по-прежнему интересует лишь величина ЭДС, (35) имеет смысл записать так:

Таким образом, становится очевидно, что ЭДС индукции максимальна на том участке, на котором больше отношение ΔФ/Δt, взятое по модулю.

Рассчитаем ЭДС индукции для каждого участка:

Таким образом, ЭДС индукции максимальна на участке 4-5, а минимальна – на участке 1-2.

Ответ: ЭДС индукции максимальна на участке 4-5, а минимальна – на участке 1-2.

8.

В цепи на рисунке 4 амперметр показывает ток I = 1,5 A. Ток, текущий через сопротивление R₁ равен I₁ = 0,5 A. Сопротивление R₂ = 2 Ом, R₃ = 6 Ом. Определить сопротивление R₁, а также токи I₂ и I₃ через сопротивления R₂ и R₃.

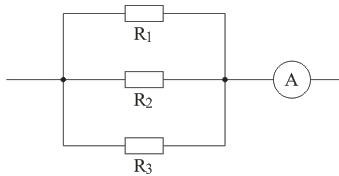
Рисунок 4

Дано:

I = 1,5 A

I₁ = 0,5 A

R₂ = 2 Ом

R₃ = 6 Ом

Найти:

R₁, I₂, I₃ - ?

Решение:

Эквивалентное сопротивление параллельно соединенных резисторов R₂ и R₃:

Схема примет вид, указанный на рисунке 5.

Тогда, по первому закону Кирхгофа, ток в сопротивлении R₂₃:

I – ток в неразветвленной части цепи;

I₁ – ток в сопротивлении R₁.

Тогда напряжение на резисторе R₂₃, равное напряжению на резисторе R₁:

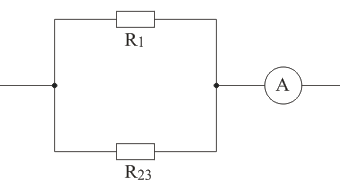
Рисунок 5

Тогда искомое сопротивление R₁:

Токи в резисторах R₂ и R₃ соответственно:

Ответ: R₁ = 3 Ом; I₂ = 0,75 A; I₃ = 0,25 A.

9.

Ток в проводнике равномерно возрастает от 0 до 2 А в течение 2 с. Определить заряд, прошедший по проводнику за это время.

Дано:

I₁ = 0

I₂ = 2 A

T = 2 c

Найти:

q - ?

Решение:

По определению, сила тока i есть производная от заряда q, прошедшего по проводнику, от времени t:

Отсюда искомый заряд:

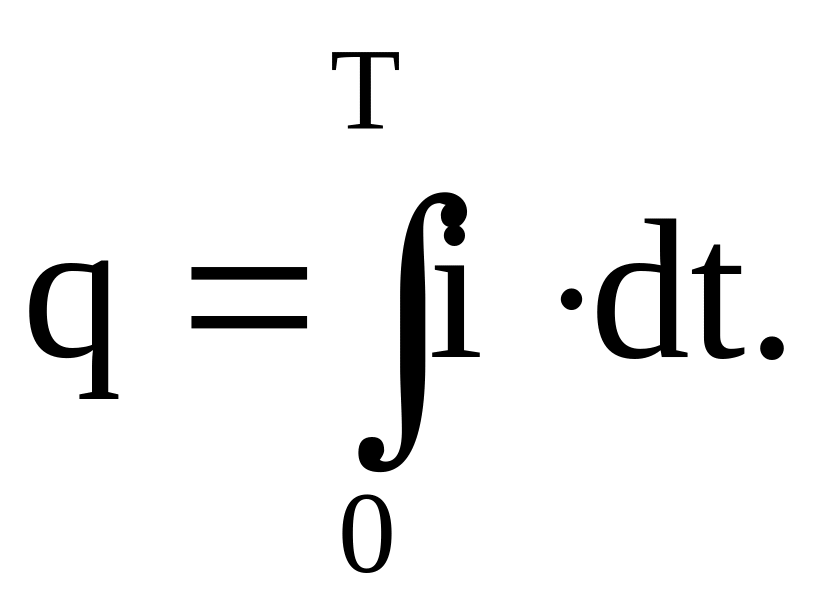
Здесь T – время прохождения тока.

Поскольку ток возрастает равномерно, закон его изменения можно записать так:

где k – постоянный коэффициент, равный:

где I₁ и I₂ – начальное и конечное значения тока. Тогда (44) примет вид:

Ответ: q = 2 Кл.

10.

Три конденсатора соединены так, как показано на рисунке 6, где U_AB = 250B, C₁ = 1,5 мкФ; C₂ = 3 мкФ; C₃ = 4 мкФ. Какой заряд и какая энергия накоплена этой батареей конденсаторов?

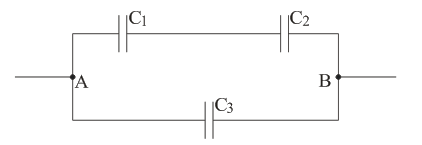
Рисунок 6

Дано:

U_AB = 250B

C₁ = 1,5 мкФ = 1,5∙10^-6 Ф

C₂ = 3 мкФ = 3∙10^-6 Ф

C₃ = 4 мкФ = 4∙10^-6 Ф

Найти:

q, W - ?

Решение:

Эквивалентная емкость последовательно соединенных конденсаторов C₁ и C₂:

Эквивалентная емкость параллельно соединенных конденсаторов C₁₂ и C₃:

Искомый заряд всей батареи:

Искомая энергия всей батареи:

Ответ: q = 1,25∙10^-3 Кл; W = 1,56∙10^-1 Дж.

11.

Электростатическое поле создано положительным точечным зарядом. Определить числовое значение градиента потенциала этого поля, если на расстоянии r = 10 см от заряда потенциал.

Дано:

r = 10 см = 0,1 м

φ

Найти:

gradφ - ?