
- •3.1. Комбинаторика
- •3.2. Комбинаторика 2
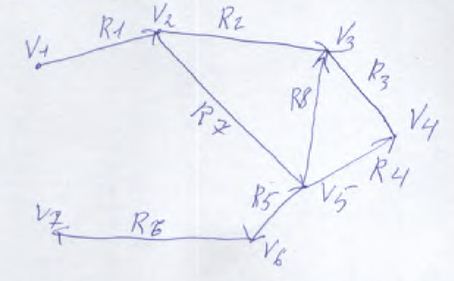
- •4. Теория графов
- •1). Матрица смежности
- •2). Функции разметки
- •3). Построить подграф являющийся остовным деревом
- •4). Матрица транзитивного замыкания.
- •6). Матрица связанности вершин
- •7). Изобразить карту графа, или убедиться что ее не существует
- •8). Проверить для графа теорему о четырех красках
- •9). Получить матрицы списков смежности вершин
- •10). Осуществить обход по ширине и глубине графа.
- •11). Преобразовать граф в ориентированный и найти матрицу отношений связанности на нем.
- •7. Основы теории чисел
6). Матрица связанности вершин
|
V1 |
V2 |
V3 |
V4 |
V5 |
V6 |
V7 |
V1 |
0 |
1 |
3 |
3 |
3 |
3 |
3 |
V2 |
1 |
4 |
3 |
3 |
3 |
3 |
3 |
V3 |
3 |
3 |
6 |
3 |
3 |
3 |
3 |
V4 |
3 |
3 |
3 |
4 |
3 |
3 |
3 |
V5 |
3 |
3 |
3 |
3 |
6 |
1 |
1 |
V6 |
3 |
3 |
3 |
3 |
1 |
0 |
1 |
V7 |
3 |
3 |
3 |
3 |
1 |
1 |
0 |
7). Изобразить карту графа, или убедиться что ее не существует
8). Проверить для графа теорему о четырех красках
9). Получить матрицы списков смежности вершин
|
V1 |
V2 |
V3 |
V4 |
V5 |
V6 |
V7 |
V1 |
- |
+ |
- |
- |
- |
- |
- |
V2 |
+ |
- |
+ |
- |
+ |
- |
- |
V3 |
- |
+ |
- |
+ |
+ |
- |
- |
V4 |
- |
- |
+ |
- |
+ |
- |
- |
V5 |
- |
+ |
+ |
+ |
- |
+ |
- |
V6 |
- |
- |
- |
- |
+ |
- |
+ |
V7 |
- |
- |
- |
- |
- |
+ |
- |
10). Осуществить обход по ширине и глубине графа.
Обход по ширине: Пара вершин, между которыми существует наибольшее количество маршрутов разной длины. Самое большое количество маршрутов (6) между вершиной V3 V3 и V5 V5. Например V5 V5:
R7, R2, R8;
R8, R2, R7;
R8, R3, R4;
R4, R2, R8;
R7, R2, R3, R4;
R4, R3, R2, R7;
Обход по глубине: самый длинный маршрут (V3 V3 (7)):
R1, R7, R8, R3, R4, R5, R6.
11). Преобразовать граф в ориентированный и найти матрицу отношений связанности на нем.
Матрица отношений связанности
|
V1 |
V2 |
V3 |
V4 |
V5 |
V6 |
V7 |
V1 |
0 |
1 |
3 |
1 |
1 |
1 |
1 |
V2 |
0 |
0 |
3 |
1 |
1 |
1 |
1 |
V3 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
V4 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
V5 |
0 |
0 |
2 |
1 |
0 |
1 |
1 |
V6 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
V7 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
