33. Метод анализа иерархий Саати.

Среди сложных методов принятия решений при многих критериях особое место занимает метод анализа иерархий Саати. Он активно применяется в различных областях человеческой деятельности со времени его появления до наших дней. О нём очень много, как теоретических, так и практических материалов в литературе и в Интернете.

Этот метод разработан американским математиком Томасом Саати, который написал о нем книги, разработал программные продукты и в течение 20 лет проводит симпозиумы ISAHP (англ. International Symposium on Analytic Hierarchy Process). МАИ широко используется на практике и активно развивается учеными всего мира. В его основе наряду с математикой заложены и психологические аспекты. МАИ позволяет понятным и рациональным образом структурировать сложную проблему принятия решений в виде иерархии, сравнить и выполнить количественную оценку альтернативных вариантов решения. Метод Анализа Иерархий используется во всем мире для принятия решений в разнообразных ситуациях: от управления на межгосударственном уровне до решения отраслевых и частных проблем в бизнесе, промышленности, здравоохранении и образовании.

Первый шаг МАИ – построение иерархической структуры, объединяющей цель выбора, критерии, альтернативы и другие факторы, влияющие на выбор решения. Построение такой структуры помогает проанализировать все аспекты проблемы и глубже вникнуть в суть задачи. Эта структура отражает понимание проблемы лицом, принимающим решение. Каждый элемент иерархии может представлять различные аспекты решаемой задачи, причем во внимание могут быть приняты как материальные, так и нематериальные факторы, измеряемые количественные параметры и качественные характеристики, объективные данные и субъективные экспертные оценки […]. Мы можем использовать иерархию как инструмент для обработки и восприятия больших объемов информации. По мере проектирования этой структуры у нас формируется все более полное понимание проблемы.

Следующим этапом анализа является определение приоритетов, представляющих относительную важность или предпочтительность элементов построенной иерархической структуры, с помощью процедуры парных сравнений. Безразмерные приоритеты позволяют обоснованно сравнивать разнородные факторы, что является отличительной особенностью МАИ.

На заключительном этапе анализа выполняется синтез (линейная свертка) приоритетов на иерархии, в результате которой вычисляются приоритеты альтернативных решений относительно главной цели. Лучшей считается альтернатива с максимальным значением приоритета.

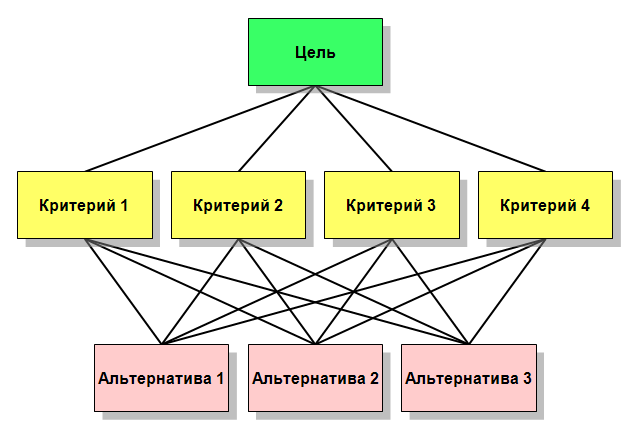
Рис. Простейшая иерархия МАИ.

Рассмотрим использование МАИ на простейшем примере.

Предположим, что для принятия УР надо выбрать одну из двух альтернатив а1 и а2.

1. Для сравнения альтернатив Т. Саати предлагает использовать шкалу относительной важности, в которой:

1 – одинаковая важность;

3 – умеренное превосходство;

5 – существенное превосходство;

7 – значительное превосходство;

9 – очень сильное превосходство,

а 2, 4, 6, 8 – промежуточные суждения.

2. На основе мнения экспертов составим матрицу сравнения критериев К1и К2, по которым оценивается важность альтернатив. Эксперты утверждают, К1 существенно превосходит по важности К2.

Кроме того, рассчитываем значения собственного вектора этой матрицы. Для этого найдём среднее геометрическое значений матрицы в каждой из строк

; ;

Найдём значения весовых коэффициентов критериев. Для этого нормируем значения собственного вектора:

2,24/(2,24+0,45)=0,83; 0,45/(2,24+0,45)=0,17.

Как матрицу, так и результаты расчётов помещаем в таблицу…

Критерии	К1	К2	Собственный вектор	Веса критериев
К1	1	5	2,24	0,83
К2	1/5	1	0,45	0,17

Отсюда видно, что матрица диагональная, а также то, что в левой нижней ячейке матрицы стоит число, обратное мнению экспертов относительно важности критериев – 1/5. Это искусственное число, которое необходимо Саати для нахождения собственного вектора матрицы и для проведения расчётов, окончательный смысл и необходимость которых будет понятна в дальнейшем.

3. Далее сравним альтернативы а1 и а2 сначала по 1-му критерию с, а затем по 2-му критерию К2. Причём, как и ранее, для каждой матрицы сравнения произведём расчеты собственных векторов и весовых коэффициентов. Результаты сравнения и расчетов приведены в таблицах …

Для критерия К1

Альтернативы	а1	а2	Собственный вектор	Веса альтернатив
а1	1	1/4	0,5	0,2
а2	4	1	2,0	0,8

Для критерия К2

Альтернативы	а1	а2	Собственный вектор	Веса альтернатив
а1	1	3	1,73	0,75
а2	1/3	1	0,59	0,25

4.Полченные результаты позволяют рассчитать интегральные оценки W1 и W2 для каждой из альтернатив. Приведём эти расчёты:

W1 = 0,83×0,2 + 0,17×0,75 = 0,29;

W2 = 0,83×0,8 + 0,17×0,25 = 0,71.

Отсюда следует УР: «Выбираем альтернативу а2, т.к. 0,71>0,29».

Для пояснения ещё одной очень важной особенности МАИ приведём ещё одну учебную задачу, предложенную Саати. Это задача связана с покупкой дома.

Из 3-х домов А, В и С надо выбрать лучший по 8-ми критериям. Эти критерии сравнивают эксперты по приведённой ранее девятибалльной шкале важности. Матрица сравнения приведена ниже

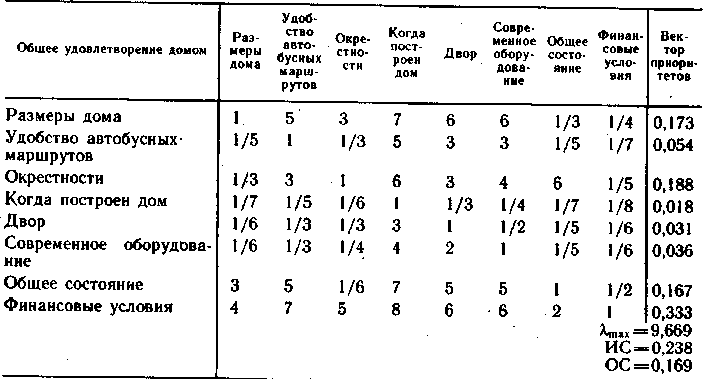
Здесь вместо весов критериев употреблён термин «вектор приоритетов». Мы видим, что наибольшим приоритетом для покупателей является стоимость дома. Кроме того, рассчитаны показатели λmax, индекс согласованности ИС и отношение согласованности ОС.

λmax вычисляется как сумма произведений, получаемая умножением суммы чисел, составляющих столбцы матрицы на соответствующие элементы, составляющие вектор приоритетов, т.е. (1+1/5+1/3+1/7+1/6+1/6+3+4)×0,173+… для всех остальных столбцов и составляющих вектора приоритетов. λmax всегда больше n, где n – размерность матрицы. В данном случае n = 8.

Индекс согласованности ИС=(λmax – n)/(n – 1) говорит о том, насколько согласованы мнения экспертов в данном случае относительно важности критериев.

Чтобы оценить эту деятельность, надо найти отношение согласованности ОС=ИС/ИС_табл, т.е. сравнить ИС с идеальным значением. ИС_табл находят как отношение согласованности для псевдослучайной матрицы, в которую входят числа 9, 8, 7, … , 1, 1/2, 1/3, … , 1/9. Саати приводит результаты расчёта усреднённых ИС_табл для различных n. Эти результаты даны в следующей таблице…

n	3	4	5	6	7	8	9
ИСтабл	0,58	0,9	1,12	1,24	1,32	1,41	1,45

По мнению Саати, если ОС>20%, то мнения экспертов не согласованы и с ними должна быть проведена дополнительная работа по разъяснению поставленной проблемы. Если же и в этом случае будет неудовлетворительный результат, то менеджер должен изменить состав экспертов.

Следующий этап решения данной задачи связан со сравнением домов по каждому из критериев. Результаты экспертного ранжирования и аналитических расчетов приведены в таблице …

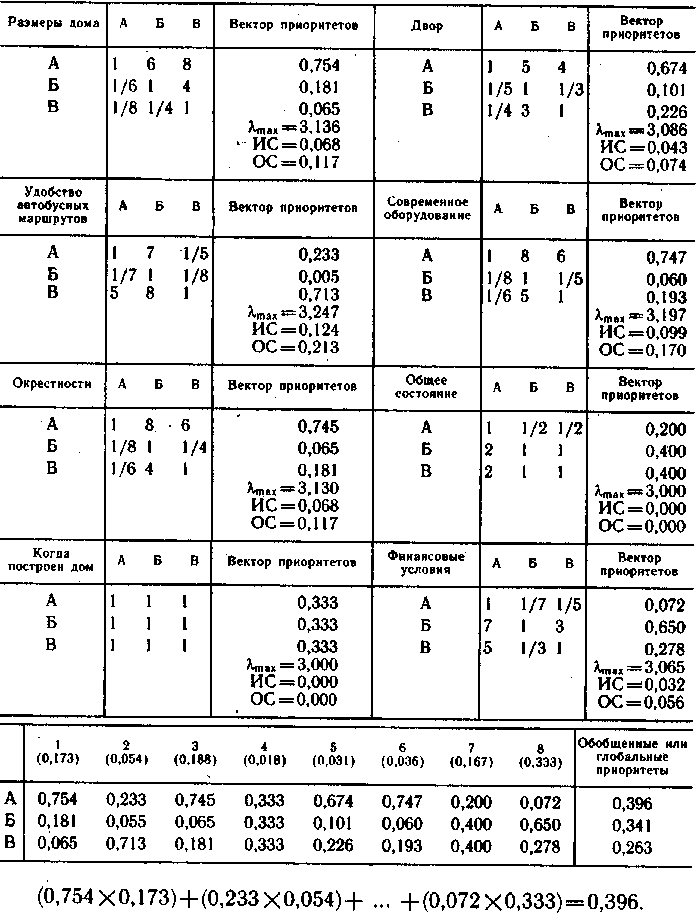
Рассчёт интегральных оценок для каждого из домов (А,В и С) приведён в таблице

	1 (0,173)	2 (0,054)	3 (0,188)	4 (0,018)	5 (0,031)	6 (0,036)	7 (0,167)	8 (0,333)	Обобщённые или глобальные приоритеты
A Б В	0,754 0,181 0,065	0,233 0,055 0,713	0,745 0,065 0,181	0,333 0,333 0,333	0,674 0,101 0,226	0,747 0,060 0,193	0,200 0,400 0,400	0,072 0,650 0,278	0,396 0,341 0,263

Указанные расчёты производились путём сложения произведений соответствующих дому А элементов векторов приоритетов из таблицы … на элементы вектора приоритетов из таблицы …

(0,754×0,173)+(0,233×0,054)+ … +(0,072×0,333)=0,396

При этом оказалось, что дом А имеет более высокий глобальный приоритет, т.е. его выбор предпочтительнее.

В заключение хочется отметить, что изобрести такой метод мог только редкий человек, в котором сочетается гуманитарная и аналитическая направленность. Именно такого сочетания обычно не хватает менеджеру.

Об этом говорит в первую очередь экспертно-аналитическая направленность данного метода.