31. Принятие ур в условиях риска и неопределенности.

УР всегда спроектировано в будущее. Мы заранее не знаем, как будут развиваться события, и как будет изменяться ситуация. То есть мы находимся в состоянии неопределённости. Причинами же неопределенности являются:

• незнание (непонимание ситуации, неполнота или отсутствие данных об обстановке);

• случайность;

• противодействие (конфликт, сопротивление).

Принятие решений в условиях неопределенности приводит к феномену, который называют риском. Тем не менее, риск и неопределённость – это разные понятия. Необходимости их разделения подчёркнута в работе Ф. Найта «Риск, неопределённость и прибыль» (1921). Он считает главным отличием то, что риск – измерим, а неопределённость – неизмерима. Однако, это не так. Формально для решения задач с риском используется теория игр (Д.Ф.Нейман), а для задач с неопределённостью (они возникают когда не известны вероятности исходов) – теория статистических решений.

Заметим, что для решений задач детерминированного характера, когда причина риска – незнание, необходимо сделать попытку сбора недостающей информации.

Под риском понимается «действие наудачу в надежде на счастливый исход». Из этого краткого определения следует, что ему, с одной стороны, сопутствует неопределенная обстановка, с другой стороны, есть надежда на успех, которую можно оценить с той или иной вероятностью удачи.

Риск – возможная опасность потерь …

Можно рассматривать риск как историческую и экономическую категорию. В последнем случае это событие, которое может произойти, а может и не произойти. Любое событие может иметь три экономических результата: отрицательный (проигрыш, ущерб, убыток); нулевой; положительный выигрыш, выгода, прибыль.

Риск – следствие неопределённости ситуации.

Функции риска

Известно, что риску присущи стимулирующая и защитная функции. Стимулирующая функция имеет конструктивный (создание защищающих инструментов и устройств) и деструктивный (авантюризм, волюнтаризм) аспекты.

Защитная функция тоже имеет два аспекта: историко-генетический (поиск средств защиты) и социально-правовой (необходимость законодательного закрепления понятия «правомерность риска»).

В психологии термин риск связан с тремя направлениями исследований:

1. Риск, как мера ожидаемой неудачи в деятельности. Вес риска определяется, как произведение вероятности неуспеха на степень неблагоприятных последствий.

2. Риск как действие, грозящее субъекту определёнными потерями (проигрышем, заболеванием, иным ущербом). Различают мотивированный риск, предполагающий получение ситуативных преимуществ в деятельности, немотивированный риск, не имеющий рационального основания; оправданный и неоправданный риск.

3. Риск, как ситуация выбора. Выбор должен быть осуществлён между менее привлекательной, но более надёжной стратегией, и более привлекательной, но менее надёжной («Синица в руках или журавль в небе»).

Склонность к риску представляет собой довольно устойчивую характеристику индивида и связана с такими личностными чертами, как импульсивность, независимость, стремление к успеху, склонность к доминированию. На рисковое поведение оказывает влияние также и культура и социальные условия.

Антиподом риска являются гарантии. Выделяют гарантии достижения (рассчитаны на успех) и гарантии компенсации (рассчитаны на неудачу).

Перед принятием УР надо провести качественный и количественный анализ рисков.

Исследование риска надо проводить в следующей последовательности:

• выявление объективных и субъективных факторов, влияющих на конкретный вид риска;

• качественный анализ выявленных факторов;

• оценка конкретного вида риска с финансовых позиций;

• установка допустимого уровня риска;

• разработка мероприятий по снижению риска при принятии УР.

Качественный анализ можно, например, провести с помощью причинно-следственной диаграммы (см. вопрос …). При этом как следствие рассматривается рисковая ситуация, а причины – это факторы риска и обстоятельства, приводящие к данной рискованной ситуации. Напомним, что для получения этой диаграммы проще всего использовать мозговой штурм. Помощь экспертов целесообразна как для построения диаграммы, так и для ранжирования факторов, влияющих на рисковую ситуацию (перед ранжированием надо выделить наиболее существенные факторы, например, путём опроса работников и экспертов).

Специальными приёмами управления риском занимается риск-менеджмент.

Основные приёмы снижения степени риска:

• получение дополнительной информации о ситуации принятия решения;

• передача риска страховой компании;

• резервирование средств (самострахование) – создание обособленных фондов возмещения убытков за счёт части собственных оборотных средств;

• диверсификация – процесс распределения инвестируемых средств между различными объектами вложения, которые непосредственно не связаны между собой;

• избегание риска, т. е. уклонение от мероприятий, связанных с риском;

• удержание риска – оставление его за инвестором (покрытие убытков за его счёт);

• лимитирование – установление системы ограничений как сверху, так и снизу на суммы расходов, продажи, кредита.

Количественный анализ риска связан с оценкой степени риска, которая определяется вероятностью наступления функции потери p_i, а также возможного ущерба от него.

Риск – динамичное явление, выбор той или иной альтернативы дает результаты, существенно зависящие от обстановки. Обстановка определяется всеми возможными при данной альтернативе исходами. Выбор наилучшего решения в условиях данных об обстановке существенно зависит от того, какова сте­пень этой неопределенности. В зависимости от этого обычно различают два вари­анта решений:

1. Выбор наилучшего решения, когда вероятности возмож­ных вариантов обстановки известны или о них можно сделать допустимые предположения.

В этом случае должно избираться решение, при котором среднее ожидаемое значение выигрыша максимально.

Согласно теории игр ожидаемый выигрыш (математическое ожидание выигрыша)

ЕV = ∑p_iWi,

где р_i – вероятность исхода, а Wi – выигрыш (потери) при i-м исходе, причём ∑p_i = 1.

Таким образом, выбор приемлемой альтернативы в условиях риска предполагает просчет возможных их вариантов с учетом вероятностей возможных исходов, выигрышей и/или потерь. Субъективное отношение к риску учитывается функциями полезности, причём в этом случае вместо ожидаемого выигрыша для каждой альтернативы может быть аналогично рассчитана ожидаемая полезность EU = ∑p_iUi.

2. Выбор наилучшего решения, когда вероятности возмож­ных вариантов обстановки неизвестны или о них можно сделать допустимые предположения. Например, можно считать, что они равны (Принцип независимости Лапласа).

Степень риска кроме математического ожидания оценивается ещё и вариацией возможного результата. При выборе альтернатив, если есть возможность, надо учитывать не только ожидаемые прибыли, но и их средне квадратичные отклонения, либо коэффициенты вариации.

Когда вероятности исходов р_i неизвестны рекомендации по выбору альтернатив вырабатываются методами теории статистических решений. Ситуация становится более неопределённой. Задачи выбора альтернатив в этом случае называются задачами с неопределённостью.

Здесь возможны три случая:

• может потребоваться гарантия, что выигрыш в любых условиях окажется не меньше, чем наибольший возможный в худших условиях. Это линия поведения по принципу "рас­считывай на худшее". Оптимальным решением в данном случае будет то, для которого выигрыш окажется максимальным из мини­мальных при различных вариантах обстановки (максиминный критерий Вальда).

• может иметь место требование в любых услови­ях избежать большого риска. Здесь оптимальным решением будет то, для которого риск, максимальный при различных вариантах обстановки, окажется минимальным (критерий минимаксного риска Сэвиджа).

• можно остановиться между лини­ей поведения "рассчитывай на худшее" и линией поведения "рассчи­тывай на лучшее" ( критерий пессимизма-оптимизма Гурвица).

Рассмотрим задачу выбора альтернатив в условиях риска и неопределённости на следующем примере.

Модель газетного киоска.

Киоскёр принимает решение относительно количества закупаемых журналов. Есть 4-ре альтернативы. 1-я – не закупать журнал; 2-ая – закупить один журнал; 3-я – закупить два журнала; 4-ая – закупить три журнала. Предварительно киоскёром изучен спрос на журнал. Оказывается, что с вероятностью p₀=0,1 отсутствует спрос на этот журнал (С=0); с p₁=0,3 имеется спрос на один журнал (С=1); с p₂=0,4 имеется спрос на два журнала (С=2); с p₃=0,2 имеется спрос на три журнала (С=3).

Доход от торговли зависит от закупочной и продажной цен на журнал, а также связан с тем сколько покупателей привыкли пользоваться этим киоском для покупки данного журнала. Для его расчёта будем использовать понятие «платёж».

Платёж = 75 × Nпр.ж – 40 × Nзак.ж – 50 × Nнеуд.спр.

Здесь 75 руб. – продажная цена журнала; 40 руб. – его закупочная цена; 50 руб. – потери киоска, связанные с неудовлетворённым спросом покупателей (результат маркетингового анализа).

В результате получаем следующую платёжную матрицу:

Табл. Платёжная матрица

УР. Закупить журналов	Состояние природы
	С=0; p0=0,1	С=1; p1=0,3	С=2; p2=0,4	С=3; p3=0,2
0	0 ( 0 )	- 50 ( 85 )	- 100 ( 170 )	- 150 ( 255 )
1	- 40 ( 40 )	35 ( 0 )	- 15 ( 85 )	- 65 ( 170 )
2	- 80 ( 80 )	- 5 ( 40 )	70 ( 0 )	20 ( 85 )
3	- 120 ( 120 )	- 45 ( 80 )	30 ( 40 )	105 ( 0 )

Под состоянием природы (термин, принятый в теории игр) мы понимаем спрос на журналы. Значения платежей, вычисленные по формуле ( ) записаны в соответствующих ячейках таблицы. В скобках даны значения риска. Риск считается равным нулю при данном спросе в том случае, когда платёж будет максимальный. Остальные значения риска находятся вычитанием текущего платежа в данном столбце из его max значения.

Рассчитаем ожидаемый выигрыш для каждой из альтернатив:

Альтернативы (закуплено журналов)	Ожидаемый выигрыш
0	ЕV0=0х0,1+(-50)х0,3+(-100)х0,4+(-150)х0,2=-85
1	ЕV1= - 12,5
2	ЕV2= 22,5
3	ЕV3= 7,5

Поскольку ЕV₂ имеет max значение выбираем 3-ю альтернативу, т.е. закупку киоскёром 2-х журналов.

Точно также можно для каждой из альтернатив сосчитать математическое ожидание риска

Альтернативы (закуплено журналов)	Ожидаемый риск
0	ЕR0=0х0,1+85х0,3+170х0,4+225х0,2=144,5
1	ЕR1= 72
2	ЕR2= 37
3	ЕR3= 52

Поскольку ЕR₂ имеет min значение, так же, как в предыдущем случае выбираем 3-ю альтернативу.

Предположим, что вероятности состояний природы (спроса) р_i неизвестны. В этом случае мы имеем задачу с неопределённостью.

Если применить максиминный критерий Вальда, то сначала для каждой альтернативы мы выбираем худший платёж (рассчитываем на худшее). Максимальный из этих платежей определяет ту альтернативу, которой мы отдаём предпочтение:

Альтернативы (закуплено журналов)	min
0	- 150
1	- 65	max
2	- 80
3	-120

Если применить критерий минимаксного риска Сэвиджа то сначала для каждой альтернативы мы выбираем состояния природы, дающие наибольший риск (избегай наибольшего риска). Минимальный из этих рисков определяет ту альтернативу, которой мы отдаём предпочтение:

Альтернативы (закуплено журналов)	max
0	225
1	170
2	85	min
3	120

Критерий пессимизма-оптимизма Гурвица.

Этот критерий используется, если требуется остановиться между линией поведения в расчёте на худшее и линией поведения в расчёте на лучшее.

В этом случае предпочтение отдаётся варианту решений, для которого окажется максимальным следующий показатель:

G = k × min a_ij + (1-k) max a_ij, где

k – коэффициент, рассматриваемый как показатель оптимизма (0 ≤ k ≤ 1). Если k=0 – можно рассчитывать на лучшее, k=1 – рассчитывай на худшее;

a_ij – выигрыш, соответствующий i-му решению при j-ом варианте обстановки.

Нетрудно убедиться, что при k=1 критерий Гурвица совпадает с критерием Вальда. Значение k=0 соответствует предельному риску. Значения k между 0 и 1 являются промежуточными между риском и осторожностью и выбираются в зависимости от конкретной обстановки и склонности к риску лица, принимающего решение.

Принятие УР в условиях неопределённости с учетом статистических характеристик результатов деятельности.

Предположим, что необходимо сравнить два проекта, реализация которых происходит в условиях неопределённости. На практике для сравнительной характеристики проектов, особенно в инвестиционно-финансовой сфере, в качестве количественных критериев используют среднее ожидаемое значение результата деятельности и среднеквадратическое отклонение σ как мера изменчивости возможного результата.

В общем случае могут быть следующие соотношения между _i и σ_i по вариантам, когда должно быть отдано предпочтение варианту А:

_А > _Б, σ_А = σ_В;

_А > _Б, σ_А < σ_В;

_А = _Б, σ_А < σ_В;

и, соответственно, варианту В:

_А < _Б, σ_А = σ_В;

_А < _Б, σ_А > σ_В;

_А = _Б, σ_А > σ_В;

Могут быть еще два спорных варианта:

_А > _Б, σ_А > σ_В;

_А < _Б, σ_А < σ_В.

В этих случаях в литературе нет единого мнения о порядке выбора более эффективного проекта. Инвестор, например, может предпочесть вариант с большим ожидаемым доходом и, соответственно, с большим риском (1), или вариант с меньшим доходом и, соответственно, с менее рискованный.

Более строгий подход основан на выборе проекта, обеспечивающего меньший коэффициент вариации (V = σ/ ), т.е. соответственно более благоприятное соотношение риска и дохода.

При этом необходим дополнительный анализ.

Предположим, что величина дохода имеет нормальный закон распределения. Тогда X = ± tσ, где t – характеризует доверительную вероятность.

При t = 1 с вероятностью 68% можно утверждать, что значение дохода лежит в пределах ± σ. При t = 3 вероятность того, что значение дохода лежит в пределах ± 3σ, составляет 99,73%.

Если ЛПР известна (или принята) требуемая доверительная вероятность и, как следствие, соответствующее ей значение t, то менее рискованным следует признать вариант, который обеспечивает равенство

X = – tσ = max.

Использование этого выражения даёт возможность на основании выбора значения t варьировать величиной доверительной вероятности, с которой обеспечивается выбор менее рискованного варианта. Так, если необходимо обеспечить гарантию выбора лучшего результата, принимают t = 3. Тогда X_{i min}= max, то есть предпочтение следует отдать варианту, который обеспечивает максимальное значение дохода из всех возможных минимальных. Нетрудно видеть, что предложенный критерий совпадает с рассмотренным ранее критерием Вальда. Уменьшая значения t, мы увеличиваем значение риска, но вместе с тем получаем более высокую среднюю отдачу.

Существует также прямая связь между t и параметром k в выражении для значения отдачи по критерию Гурвица: k = (t + 3)/6.

Использование дерева решений при принятии УР.

Дерево решений – это графическое средство анализа альтернатив в условиях риска. Оно используется в том случае, когда решение можно представить в виде иерархии его промежуточных этапов. Дерево решений строится обычно при помощи ЭВМ на основе матрицы платежей. При этом вычислительная машина рассчитывает ожидаемые выигрыши, отображает их на ветвях иерархического дерева и на их основе выбирает лучшую альтернативу.

Рассмотрим пример дерева решений (см. рис. ). Он касается выбора альтернатив выдачи ссуды. Она либо выдаётся, либо не выдаётся, либо операции с ней происходят после аудиторской проверки. Здесь этапы принятия решения обозначены квадратиками, а возможные альтернативы обозначены кружками. Ожидаемые выигрыши отображены около кружков в скобках, а их значения, соответствующие выбранному решению над квадратиками. Например, над квадратиком 2 находится

1905=(17250-15000)х0,98+(-15000)х0,02.

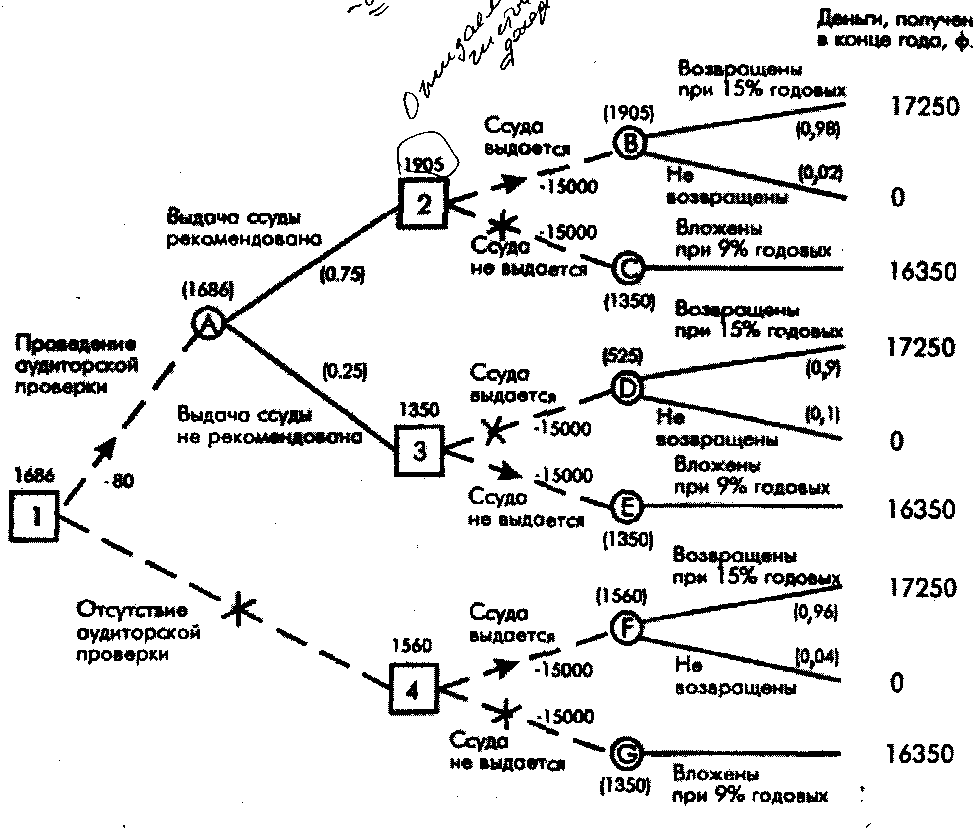
Рис. Дерево решений

И все же риск допустим только в пределах правового поля. В кодексе законов о труде он признается правомерным лишь при одновременном наличии следующих четырех условий: риск должен соответствовать значению той цели, для которой он предпринимается; цель эта не может быть достигнута обычными нерискованными средствами; риск не должен переходить в заведомое причинение ущерба; объектом риска, как правило, могут являться материальные, вещественные факторы, но не жизнь и здоровье человека.

Нарушение хотя бы одного из этих условий исключает правомерность риска.