3 Обернена функція

Розглянемо функцію, задану формулою , де – довільне дійсне число, відмінне від нуля; аргумент може набувати не тільки додатних, а й від’ємних значень.

Наприклад, дано функцію Область її визначення всі дійсні числа, окрім (бо на 0 ділити не можна). Складаємо таблицю значень цієї функції для кількох значень аргументу:

x	-6	-5	-4	-3	-2	-1	0	1	2	3	4	5	6
y	-1	-1,2	-1,5	-2	-3	-6		6	3	2	1,5	1,2	1

Позначимо точки, координати яких наведено в таблиці (рис. 3.1). Коли б на цій самій координатній площині позначили більше точок, координати яких задовольняють рівність вони розмістилися б, як показано на (рис. 3.1). Якщо для кожного дійсного значення , крім , за формулою обчислити відповідне значення і нанести всі точки з одержаними координатами на координатну площину, матимемо графік даної функції (рис. 3.1 ). Таку лінію називають гіперболою. Гіпербола складається з двох гілок.

Рис. 3.1. Побудова графіка

Графік функції – гіпербола, симетрична відносно точки О початку координат. Її гілки розміщено в І і ІІІ координатних квадрантах. Осі координат поділяють координатну площину на чотири координатних кути, їх називають також координатними чвертями, або квадрантами, і нумерують, як показано на рис. 3.2).

Рис. 3.2. Позначення координатних квадрантів на координатній площині

Якщо таким способом побудувати графік функції , дістанемо також гіперболу; тільки її гілки розміщені в ІІ і ІV координатних квадрантах (рис. 3.3).

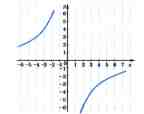
Рис. 3.3. Графік функції

Графік кожної функції , де - відмінне від нуля дійсне число, – це гіпербола, симетрична відносно початку координат (нуля координат О).

Якщо , гілки такої гіперболи розміщено в І і ІІІ координатних кутах, коли , – у ІІ та ІV.

Властивості функції для різних значень можна визначити за графіками, наведеними, наприклад, на рис. 3.1 і 3.3. Подаємо їх у вигляді табл. 3.1:

Таблиця 3.1

Властивості функції	Вид функції
Область визначення D	Усі числа, крім	Усі числа, крім
Область значень E	Усі числа, крім	Усі числа, крім
Додатні значення
Від’ємні значення
Проміжки спадання	і	-
Проміжки зростання	-	і

Функцію, задану формулою , часто називають оберненою пропорційністю (на відміну від функції , яку називають прямою пропорційністю). Раніше оберненою пропорційністю ми називали відповідність, при якій зі збільшенням однієї змінної в кілька разів значення другої зменшувалися в стільки ж разів. Так буває тільки у випадку, коли і – додатні числа. Якщо у функції число від’ємне, то зі збільшенням значень у кілька разів значення також збільшується у стільки ж разів. Це видно з рис. 3.4.

Рис. 3.4. Обернено пропорційна функція з від’ємним

Використовуючи степінь з від’ємним показником, функцію можна записати так: . Іноді її записують і у вигляді: .

Приклад. Чи є оберненою пропорційністю залежність, задана рівністю:

а) 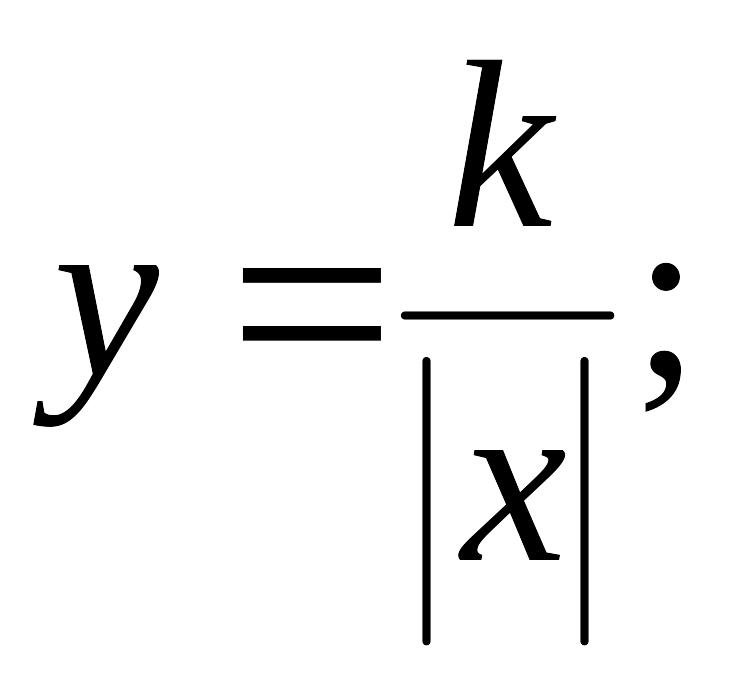б) ? Відповідь: а) Ні, б) ні.

Приведемо практичні приклади.

Завдання 1.

Функцію задано формулою . Знайдіть значення , якщо графік функції проходить через точку

Розв’язання. Підставимо значення і у формулу, якою задано функцію. Одержимо Отже, .

Завдання 2.

Розв'яжіть графічно рівняння

Розв’язання. Побудуємо в одній системі координат графіки функцій і (рис. 3.5).

Рис. 3.5. Графічне розв’язання рівняння

Ці графіки перетинаються в точках P і Q, абсциси яких дорівнюють приблизно 1 і -3. Перевіряємо, чи це точне значення, чи наближене: 1+2=3,

-3+2=-1.

Відповідь: .