
- •1. Основні поняття та властивості функціональної залежності.
- •2 Лінійна функція
- •3 Обернена функція
- •4 Степенева функція
- •5 Тригонометрична та обернена тригонометрична функції
- •7. Показникова та логарифмічна функції.
- •8. Основні можливості наочності викладання теорії функцій в курсі алгебри з використанням програмного комплексу Microsoft Mathematics 4.0
- •Висновок
- •4. Бедрій я. І. Безпека життєдіяльності. Навчальний посібник. – Київ: Кондор, 2009. – 286 с
- •Хід уроку
- •V. Підсумок уроку. Оцінювання учнів.
- •Vі. Домашнє завдання.
- •Хід уроку
- •Iіі. Актуалізація опорних знань та вмінь
- •V. Підсумки уроку
- •VI. Домашнє завдання
- •Хід уроку
- •II. Вивчення властивостей тригонометричних функцій.
- •III. Застосування властивостей тригонометричних функцій до розв'язування вправ.
- •IV. Підсумок уроку.
- •V. Домашнє завдання.
- •Хід уроку
- •1. Поняття логарифмічної функції
- •2. Графік логарифмічної функції.(Міні-дослідження)
- •3. Властивості логарифмічної функції.(Захист міні-проектів)
- •4. Властивості логарифмів чисел
- •V. Підсумок уроку
- •Vі. Домашнє завдання
- •§22 Достатній рівень № 215(1-2), 216 (1), 225(1-2);
Державний вищий навчальний заклад
«Ужгородський національний університет»
Інститут післядипломної педагогічної освіти та доуніверситетської підготовки
Пояснювальна записка
до дипломної роботи
спеціаліста
на тему
«Розвиток поняття функціональної залежності на уроках алгебри в загальноосвітній школі»
Виконала студентка 2 курсу
Напряму підготовки математика
Кус Ю. А.
Керівник: Орбан Ю. М.
Ужгород – 2014р.
Зміст
Вступ 3
Основні поняття та властивості функціональної залежності 5
Лінійна функція 17
Обернена функція 21
Степенева функція 25
Тригонометрична та обернена тригонометрична функції 29
Показникова та логарифмічна функції 39
Напрямки удосконалення наочності та сприйняття основних властивостей функцій в шкільній програмі курсу алгебри 42
Висновки 51
Список літератури 52
Додатки 53
Вступ
Актуальність теми дипломної роботи полягає в зростанні обсягів розділів функціонального аналізу в курсах алгебри загальноосвітньої школи, що потребує удосконалення технологічної наочності матеріалу, що викладається на базі застосування сучасної комп’ютерної техніки та технологічної можливості застосування повномасштабних проекційних та інтерактивних класних дошок, на яких з’являється можливість поетапної побудови графіків як простих функцій так складних суперпозицій декількох функцій в кольоровому режимі з використанням масштабованості та деталізації графіків в характерних точках.
Предметом дипломного дослідження є ефективність процесу формування поняття функціональної залежності в шкільному курсі алгебри в 7–11 класах, послідовність та наочність учбового матеріалу.
Об’єктом дипломного дослідження є навчальний матеріал розділів шкільних підручників з алгебри в 7–11 класах загальноосвітньої школи, присвячений формуванню поняття функціональної залежності.
Метою дипломного дослідження є узагальнення поточного стану матеріалів з алгебри в шкільних підручниках та розробка напрямків удосконалення наочності і сприйняття основних властивостей функцій в шкільній програмі курсу алгебри.
Для реалізації мети дипломного дослідження були виконані наступні завдання:
загальна сутність та основні властивості функцій;
лінійна, обернена функції
степенева функція;
тригонометричні та обернені тригонометричні функції;
показникова та логарифмічна функції.
запропоноване використання комп’ютерного професійного розрахунково-графічного пакету Microsoft Mathematics 4.0 рівня середньої школи та показана ефективність його використання в наочному викладанні матеріалів по складним функціям (сума та різниця функцій).
1. Основні поняття та властивості функціональної залежності.
Функціональна залежність – одне з найважливіших понять математики, вона дає можливість досліджувати й моделювати не тільки стани, але й процеси. Дослідження процесів і явищ за допомогою функцій – один з основних методів сучасної науки. Вивчають функції в 7, 8, 9, 10 і 11 класах загальноосвітньої школи .
Для визначення поняття функції використаємо ряд прикладів:
1. Площа квадрата залежить від довжини його сторони. Кожному значенню довжини квадрата відповідає єдине значення його площі (рис 1.1).
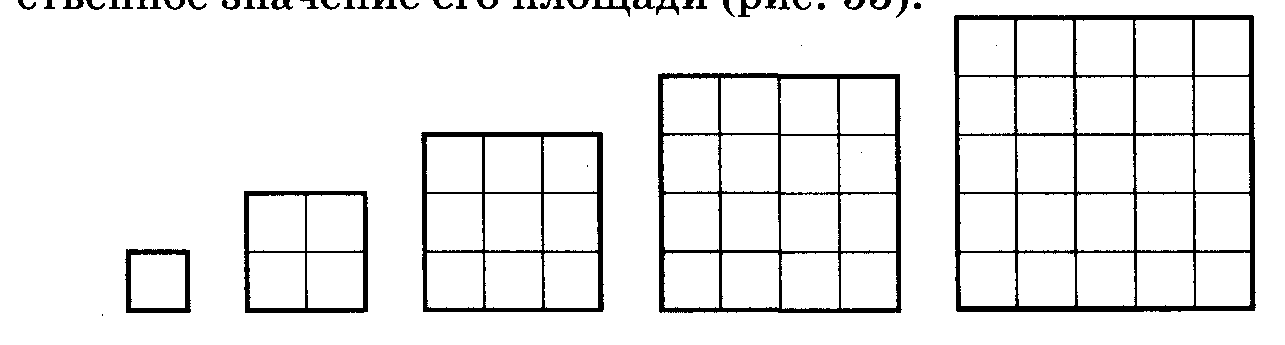
Рис. 1.1. Функціональна залежність площі квадрата від довжини його сторони
2. Кожному значенню маси вантажу, підвішеного на пружині, відповідає певна довжина пружини (рис 1.2).
3.
Маса шматка крейди залежить від його
обсягу. Кожному значенню обсягу ![]() шматка крейди відповідає єдине значення
його маси
шматка крейди відповідає єдине значення
його маси ![]() .
.
4.
Кожному значенню температури повітря
![]() відповідає єдине значення висоти
відповідає єдине значення висоти ![]() стовпчика рідини в термометрі.
стовпчика рідини в термометрі.
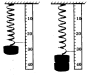
Рис. 1.2. Залежність довжини розтягнення пружини від маси вантажу
5.
Кожному значенню змінної ![]() відповідає єдине значення математичного
виразу
відповідає єдине значення математичного
виразу ![]() .
.
Прикладів залежностей між змінними можна привести багато. Для науки й практики важливо вміти досліджувати такі залежності. Їх називають функціональними залежностями.
У розглянутих прикладах мова йде про зв'язок між двома змінними. Одну з них, значення якої вибирають довільно, називають незалежною змінною, або аргументом. Іншу змінну, залежну від аргументу, називають залежною змінною, або функцією.
Незалежними змінними (аргументами) у наведених вище прикладах є: довжина сторони квадрата, обсяг шматка крейди, маса вантажу, температура повітря. Їхні значення можна вибирати довільно. Залежними змінними будуть: площа квадрата, маса крейди, довжина пружини, висота стовпчика рідини в термометрі. Найчастіше у математиці функціональна залежність задається формулами - це аналітичний спосіб задання.
Залежність між змінними x та y, в якій кожному значенню змінної x із деякої множини D відповідає єдине значення змінної y, називається функціональною залежністю, або функцією.
За
таких умов змінну
називають аргументом функції ![]() ,
множину
,
множину ![]() -областю
визначення функції.
-областю
визначення функції.
Всі
значення, які може приймати аргумент
функції
,
це область визначення аргументу (множина
).
А всі відповідні значення функції
–
область визначення функції (множина
![]() ).
).
Наприклад,
площа ![]() квадрата – це функція від довжини його
сторони
квадрата – це функція від довжини його
сторони ![]() (
(![]() ).
Тут
– функція,
-
аргумент. Область визначення цієї
функції – множину всіх позитивних
чисел.
).
Тут
– функція,
-
аргумент. Область визначення цієї
функції – множину всіх позитивних
чисел.
Висота стовпчика рідини в термометрі – функція від температури . Тут – функція, - аргумент. Нехай, наприклад, протягом доби температура повітря підвищувалася від -50 до +70, а висота стовпчика рідини в термометрі від 20 до 32 см. Цій зміні відповідає якась функція, область визначення якої є проміжок від -50 до +70, а область значення – проміжок від 20 до 32 см.
Задавати функціональні залежності можна різними способами. Часто їх задають формулами. Наприклад, відповідність між довжиною сторони квадрата і його площею можна задати формулою .
Залежність
між радіусом кола ![]() і його довжиною
і його довжиною ![]() можна задати формулою
можна задати формулою ![]() .
.
Залежність
між значеннями змінної
й значеннями функції
у вираженні
,
можна задати формулою ![]() .
.
Завдання функції формулою зручно, тому що це дає можливість знаходити значення функції для довільного значення аргументу. Таке завдання функції досить ощадливе: в основному, формула займає один рядок.
Якщо функцію задають формулою й нічого не говорять про область її визначення, то вважають, що ця область – множина всіх значень змінної, при яких формула має сенс.
Наприклад,
область визначення функції
– множина всіх чисел, а функції ![]() – множина всіх чисел, крім 1, тому що на
0 ділити не можна.
– множина всіх чисел, крім 1, тому що на
0 ділити не можна.
Задавати функцію можна й у вигляді таблиці. Наприклад функцію для перших десяти натуральних значень можна задати у вигляді такої таблиці:
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
1 |
3 |
5 |
7 |
9 |
11 |
13 |
15 |
17 |
19 |
Тут:
Область визначення аргументу: 1,2,3,4,5,6,7,8,9,10;
Область значень функції: 1,3,5,7,9,11,13,15,17,19.
Табличний спосіб завдання функції зручний тим, що для певних значень аргументу в таблицю вже занесені відповідні значення функції, тому не потрібно проводити обчислення. Незручний він тим, що таблиця займає більше місця. До того ж, як правило, містить значення функції не для всіх значень аргументу, а тільки для деяких.
Функцію можна задавати й словесно. Наприклад, якщо кожному цілому числу поставити у відповідність його квадрат, то одержимо функцію, область визначення якої є множина цілих чисел, а область значень – множина квадратів натуральних чисел і число 0.
Числовою
функцією з областю визначення
називають залежність, при якій кожному
числу
із множини
(області визначення) ставиться у
відповідність єдине число
.
Записують цю відповідність так ![]() .
.
Область
визначення функції![]() – це множина тих значень, яких може
набувати аргумент
.
Вона позначається
– це множина тих значень, яких може
набувати аргумент
.
Вона позначається ![]()
Область
значень функції
– це множина, яка складається з усіх
чисел ![]() ,
де
належить області визначення. Її позначають
,
де
належить області визначення. Її позначають
![]()
Позначення і терміни числових функцій наведені на рис. 1.3:
![]() -
Область визначення аргументу x;
-
Область визначення аргументу x;
![]() -
Область значень функції y;
-
Область значень функції y;
![]() Аргумент
(незалежна змінна);
Аргумент
(незалежна змінна); ![]() Функція (залежна змінна);
Функція (залежна змінна); ![]() Функція;
Функція;
![]() -
Значення функції
у точці
-
Значення функції
у точці ![]() .
.
Рис. 1.3. Визначення основних термінів функціональних залежностей
Графіком
функції
називається множина всіх точок
координатної площини з координатами
![]() ,
де перша координата
«пробігає»
всю область визначення функції, а друга
координата – це відповідне значення
функції
у точці
(рис. 1.4).
,
де перша координата
«пробігає»
всю область визначення функції, а друга
координата – це відповідне значення
функції
у точці
(рис. 1.4).
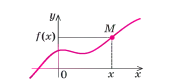
Рис. 1.4. Основні визначення «графіку функції»
Найчастіше
функцію задають за допомогою формули.
Якщо немає додаткових обмежень, то
областю визначення функції, заданої
формулою, вважають множину всіх значень
змінної, при яких ця формула має числове
визначення. Наприклад, якщо функція
задана формулою ![]() то її область визначення –
то її область визначення – ![]() ,
тобто множина аргументів функції
,
тобто множина аргументів функції ![]() а область значень -
а область значень -![]() ,
тобто множина значень функції
,
тобто множина значень функції![]() .
.
Іноді
функція може задаватися різними формулами
на різних підмножинах значень аргументу.
Наприклад, ![]()
На
рис. 1.5 графічно задана функція
з
областю визначення ![]() і множиною значень
і множиною значень ![]() .
.
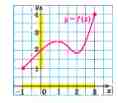
Рис. 1.5. Області визначення аргументів D(f) та значень функції E(f)
Значення,
що приймає функція
в деякій точці
множини D
на
якій ця функція задана, називається
найбільшим (найменшим) на цій множині,
якщо ні в якій іншій точці множини
функція не має більшого (меншого)
значення. Тобто для всіх ![]() виконується нерівність
виконується нерівність ![]() (відповідно
(відповідно ![]() для найменшого значення). Іноді це
записують так:
для найменшого значення). Іноді це
записують так: ![]() (відповідно
(відповідно ![]() ).
).
Наприклад,
для функції
,
графічно заданій на відрізку ![]() на рис. 1.1.6, найменше значення дорівнює
1, а найбільше 4. Тобто
на рис. 1.1.6, найменше значення дорівнює
1, а найбільше 4. Тобто ![]()
![]() .
.
Функція ![]() називається парною,
якщо для будь-якого х з
області визначення функції виконується
рівність
називається парною,
якщо для будь-якого х з
області визначення функції виконується
рівність ![]() .
.
Розглянемо приклади деяких характерних графіків функцій та типів специфічного завдання аргументів функцій.
На
рис. 1.6 наведений графік функції
модуля аргументу ![]() ,
який представляє парну функцію, симетричну
відносно осі
,
який представляє парну функцію, симетричну
відносно осі ![]() .
.
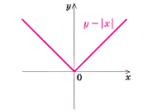
Рис. 1.6. Графік функції модуля аргументу
На
рис. 1.7 наведений графік функції цілої
частини аргументу ![]() де
де ![]() – позначення цілої частини числа
,
тобто найбільшого цілого числа, яке не
перевищує
який представляє непарну функцію,
симетричну відносно осі
– позначення цілої частини числа
,
тобто найбільшого цілого числа, яке не
перевищує
який представляє непарну функцію,
симетричну відносно осі ![]() .
.
Функція
називається непарною,
якщо для будь-якого х з
області визначення функції виконується
рівність ![]() .
.
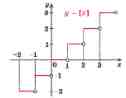
Рис. 1.7
Графік функції цілої частини аргументу
![]()
Область
визначення цієї функції ![]() – множина всіх дійсних чисел, а область
значень
– множина всіх дійсних чисел, а область
значень ![]() -
множина всіх цілих чисел.
-
множина всіх цілих чисел.
На
рис. 1.8 наведено графік числової
функції дробової частини аргументу
![]() ,
де
,
де ![]() – позначення дробової частини числа
(за означенням
– позначення дробової частини числа
(за означенням ![]()
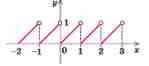
Рис. 1.8. Графік числової функції дробової частини аргументу
Одними
з найбільш важливих властивостей функцій
є їх зростаючий чи спадний характер.
Функція
є зростаючою на множині аргументів
при умовах: якщо ![]() ,
то
,
то ![]() для всіх
(при збільшені аргументу збільшується
значення функції ).
для всіх
(при збільшені аргументу збільшується
значення функції ).
Функція
є спадною на множині аргументів
:
якщо
,
то ![]() для всіх
для всіх
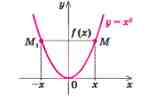
Рис. 1.9. Приклад графіка складеної зростаючої та спадної функції на окремих проміжках області визначення аргументів
Розглянемо
детальніше приклади зростаючих та
спадних функцій на окремих проміжках
визначення аргументів. На графіку
рис. 1.9 бачимо, що на всій області
визначення ця функції не є ні зростаючими,
ні спадними. Але можна виділити проміжки
області визначення, де ці функції
зростають і де спадають. Так, на проміжку
![]() функції
функції ![]() зростає а на проміжку
зростає а на проміжку ![]() – спадає.
– спадає.
Розглянемо
властивості парності і непарності
функцій, області визначення яких
симетричні відносно початку координат,
тобто разом з кожним числом
містять і число ![]() .
Для таких функцій визначено поняття
парності і непарності.
.
Для таких функцій визначено поняття
парності і непарності.
Функція
називається парною, якщо для будь-якого
з її області визначення ![]() Якщо функція
парна, то до її графіка разом з кожною
точкою
Якщо функція
парна, то до її графіка разом з кожною
точкою ![]() з
координатами
з
координатами ![]() входить також і точка
входить також і точка ![]() з координатами
з координатами ![]() .
Точки
і
розміщені симетрично відносно осі
тому й графік парної функції розміщений
симетрично відносно
.
.
Точки
і
розміщені симетрично відносно осі
тому й графік парної функції розміщений
симетрично відносно
.
Функція
називається непарною, якщо для будь-якого
з її області визначення ![]()
Якщо
функція
непарна, то до її графіка разом з кожною
точкою
з
координатами
входить також і точка
з координатами ![]() .
Точки
і
розміщені симетрично відносно початку
координат, тому й графік непарної функції
розміщений симетрично відносно початку
координат.
.
Точки
і
розміщені симетрично відносно початку
координат, тому й графік непарної функції
розміщений симетрично відносно початку
координат.
Наприклад,
функція
(тобто функція ![]() )
– парна, оскільки
)
– парна, оскільки ![]() .
Графік парної функції
симетричний відносно осі
.
.
Графік парної функції
симетричний відносно осі
.

Рис. 1.10.
Графіки парної функції
та непарної функції ![]()
Функція
(тобто функція ![]() )
– непарна оскільки:
)
– непарна оскільки: ![]() Графік непарної функції
симетричний відносно початку координат,
тобто відносно точки
Графік непарної функції
симетричний відносно початку координат,
тобто відносно точки ![]() .
.
На рис. 1.11 – 1.13 наведені принципи побудови графіків довільних функцій способами паралельного переносу, віддзеркалювання та розтягування:
функцій
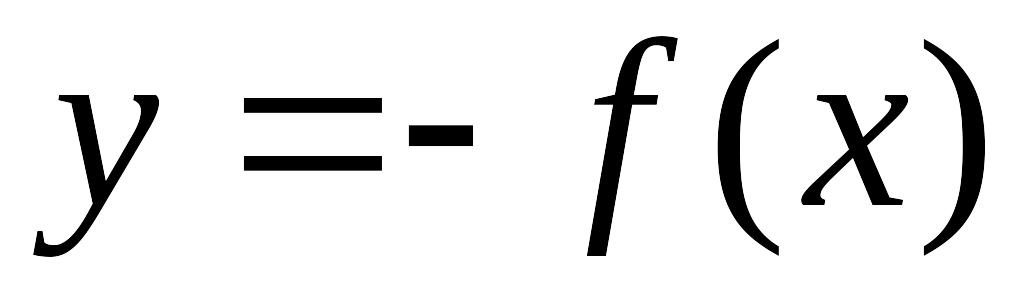 та
та 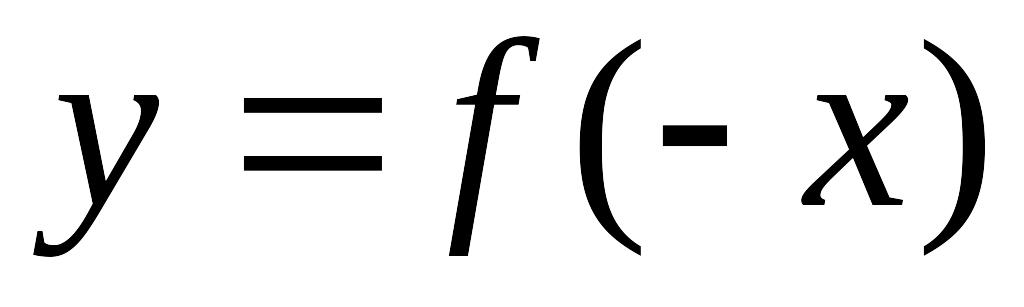 ;
;функцій
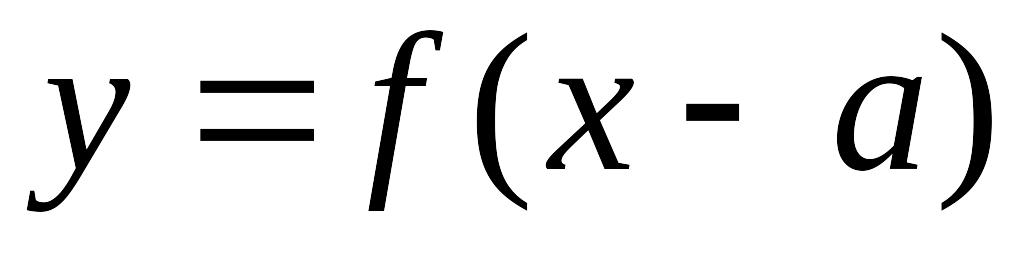 та
та 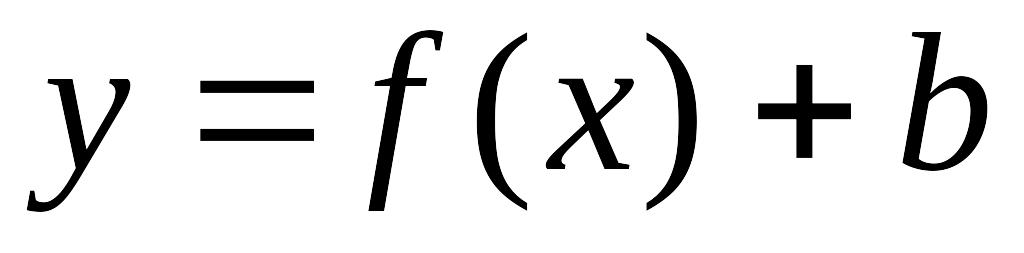 ;
;функцій
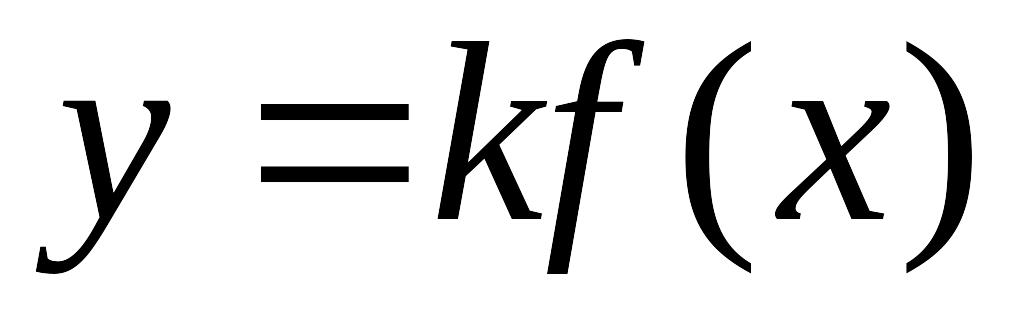 та
та 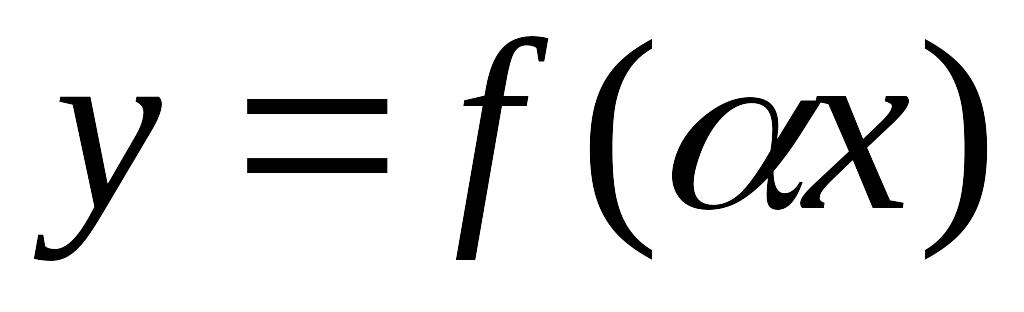
Як показує приклад, наведений на рис. 1.12:
1) графік функції y = – f (x) можна одержати з графіка функції y = f (x) його симетричним відображенням відносно осі Ox.
2) графік функції y = f (–x) можна одержати з графіка функції y = f (x) його симетричним відображенням відносно осі Oy.
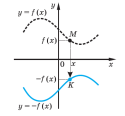
Рис. 1.11. Побудова графіків функцій та
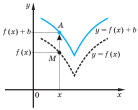
Рис. 1.12 Побудова графіків функцій та
Як показує приклад, наведений на рис. 1.12:
1) графік функції y = f (x – a) можна одержати паралельним перенесенням графіка функції y = f (x) уздовж осі Ox на a одиниць;
2) графік функції y = f (x) + b можна одержати паралельним перенесенням графіка функції y = f (x) уздовж осі Oy на b одиниць.
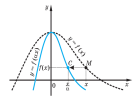
Рис. 1.13. Побудова графіків функцій та
Як показує приклад, наведений на рис. 1.13:
1) графік функції y = k f (x) (k > 0) одержується з графіка функції y = f (x) його розтягуванням (при k > 1 розтяг у k разів) або стискуванням (при 0 < k < 1 стиск у k разів) уздовж осі Oy;
2) графік функції y = f (αx) (α > 0) одержується з графіка функції y = f (x) його розтягуванням (при 0 < α < 1 розтяг у α разів) або стискуванням (при α > 1 стиск у α разів) уздовж осі Ox.
Наведемо деякі практичні завдання по викладеним темам основних властивостей числових функцій.
Завдання 1. Знайдіть область визначення функції
1)
![]()
2)![]()
3)![]()
Розв’язання:
Обмежень для знаходження виразу
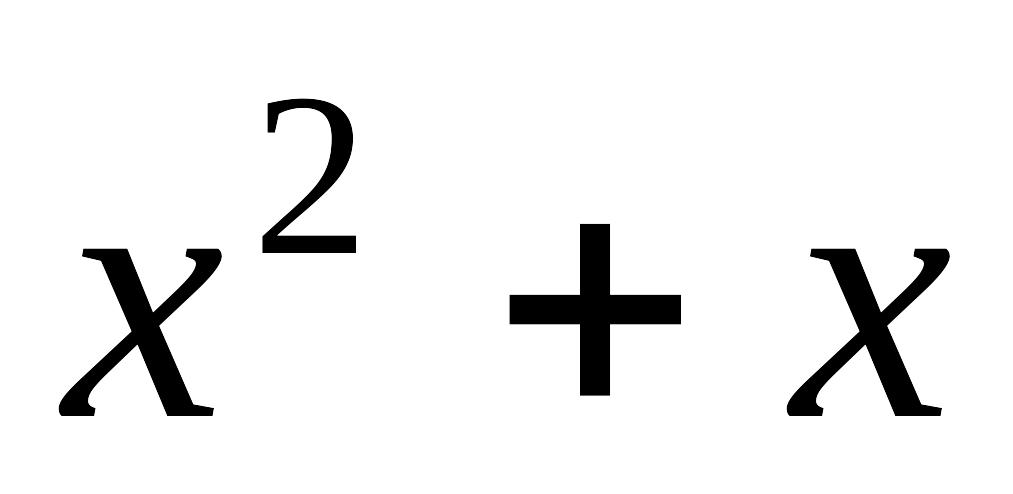 немає; отже, множина значень аргументів
немає; отже, множина значень аргументів
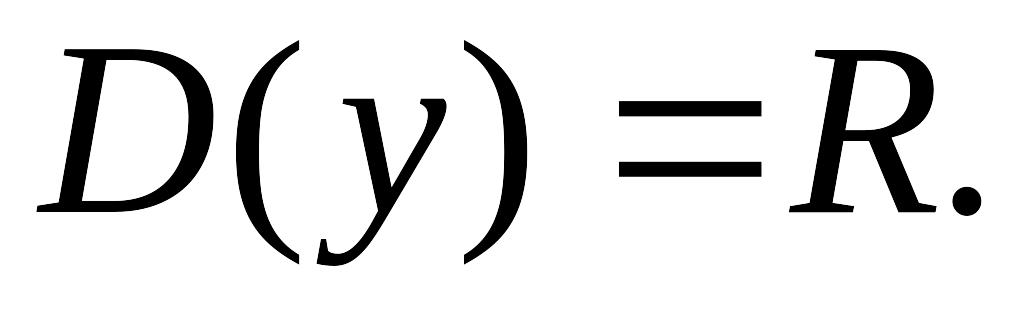 (всі дійсні числа)
(всі дійсні числа)Область визначення функції
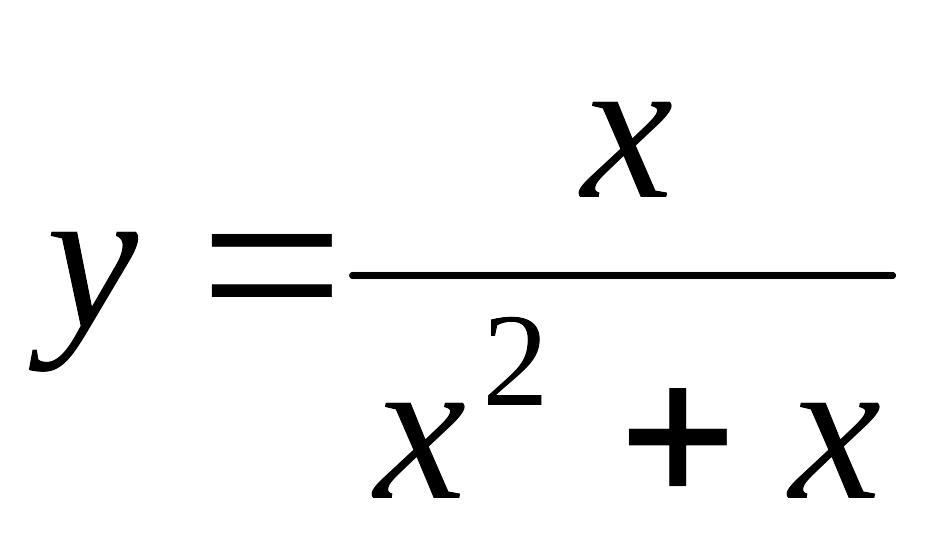 задана обмеженням
задана обмеженням 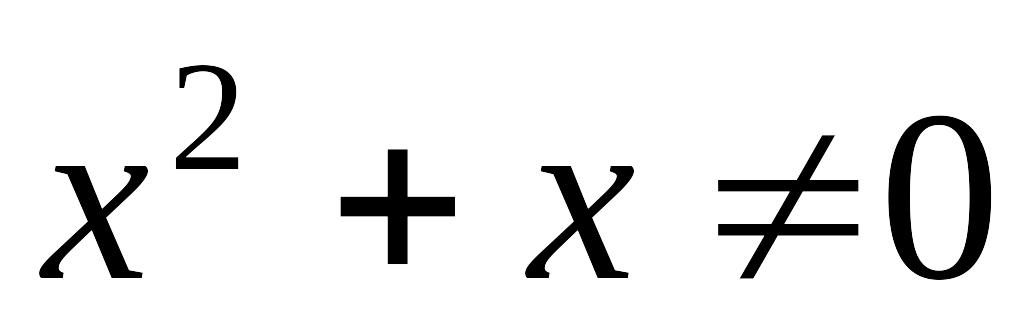 ,
оскільки знаменник дробу не може бути
дорівнювати нулю.
,
оскільки знаменник дробу не може бути
дорівнювати нулю.
З’ясуємо,
коли ![]() .
Маємо
.
Маємо ![]()
![]() або
або ![]() .
.
Тоді
область визначення можна задати
обмеженнями ![]() або записати так
або записати так ![]()
Область визначення функції
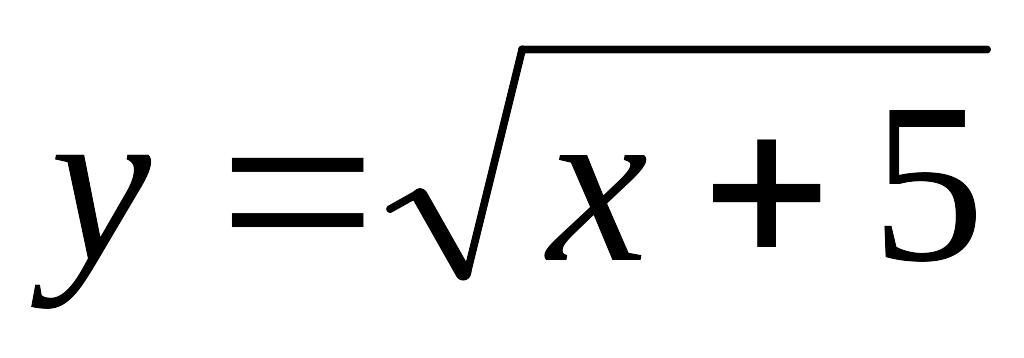 задана обмеженням
задана обмеженням
![]() ,
тобто
,
тобто ![]() ,
оскільки під знаком квадратного кореня
повинен стояти невід’ємний вираз. Отже,
,
оскільки під знаком квадратного кореня
повинен стояти невід’ємний вираз. Отже,
![]() .
.
Завдання
2.
Знайдіть область значень функції ![]()
Розв’язання:
Складаємо
рівняння ![]() .
Воно рівносильне рівнянню
.
Воно рівносильне рівнянню ![]() яке має розв’язки, якщо
яке має розв’язки, якщо ![]() ,
тобто при
,
тобто при ![]() .Усі
ці числа і складуть область значень
функції.
.Усі
ці числа і складуть область значень
функції.
Отже, область значень заданої функції
![]() (тобто
).
(тобто
).
Завдання 3. Дослідіть, які із заданих функцій є парними, які непарними, а які – ні парними, ні непарними.
1)
![]() ;
;
2)
![]() ;
;
3)![]()
Розв’язання:
1)
Область визначення функції
:
![]() ,
тобто вона не симетрична відносно точки
(точка
,
тобто вона не симетрична відносно точки
(точка ![]() входить до області визначення, а
входить до області визначення, а ![]() ні)
ні)

Рис. 1.14. Область визначення функції з розривом
Отже, задана функція (рис. 1.14) не може бути ні парною, ні непарною.
2)
Область визначення функції
:
![]() тобто вона симетрична відносно точки
тобто вона симетрична відносно точки
![]()
![]() а отже, функція парна.
а отже, функція парна.
3)
Область визначення функції ![]() :
отже, вона симетрична відносно точки
:
отже, вона симетрична відносно точки
![]()
отже, функція непарна.
