2.5 Расчет продольного ребра

2.5.1Определение нагрузок и расчетных усилий

Погонную нагрузку на плиту от веса кровли и снега собирают с грузовой площади шириной, равной ширине плиты, и суммируют с нагрузкой от веса конструкции. Для расчета плиты по предельным состояниям второй группы (на трещиностойкость и по деформациям, а также при подсчете потерь предварительного напряжения) необходимо определить величину сочетаний нагрузок: при частой комбинации и при практически постоянной комбинации.

Таким образом, с учетом расчетов п.2.1, нагрузки на плиту будут составлять:

- при основной комбинации

(g_sd+q_sd)=4.259·2.2+1,8·2.2=13.37 кН/м,

- при нормативной (редкой) комбинации

(g_sk+q_sk)=3,155·2.2+1,2·2.2=9.58 кН/м,

- при практически постоянной комбинации

(g_sk+ψ₂·q_sk)=3,155·2.2+1,2·2.2·0,3=7.73 кН/м,

- при частой комбинации

(g_sk+ψ₁·q_sk)=3,155·2.2+1,2·2.2·0,5=8.26 кН/м.

ψ₁ ,ψ₂ – коэффициенты сочетаний для переменных нагрузок и воздействий.

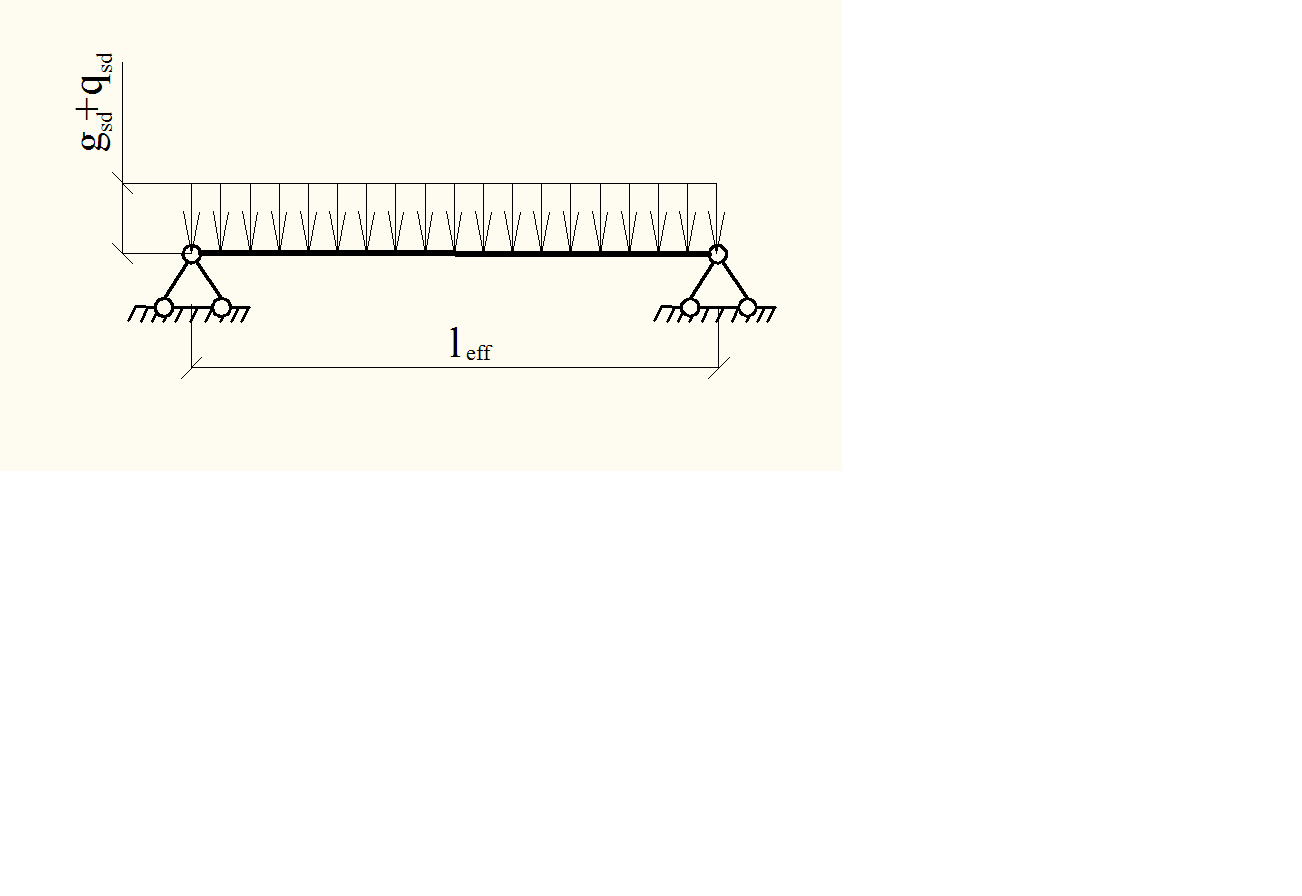
Рисунок 2.3 Расчетная схема продольного ребра

Расчетный пролет ребра – по осям опор:

l_eff=11,96-2·0,05=11,86 м.

Изгибающие моменты:

- при основной комбинации

М_sd =(g_sd+q_sd)· l_eff²/8=13.37·11,86²/8=235.08 кН·м,

- при нормативной (редкой) комбинации

М_sd =(g_sk+q_sk)· l_eff²/8=9.58·11,86²/8=168.44 кН·м,

- при практически постоянной комбинации

М_sd =(g_sk+ ψ₂·q_sk)· l_eff²/8=7.73·11,86²/8=135.91 кН·м,

- при частой комбинации

М_sd =(g_sk+ ψ₁·q_sk)· l_eff²/8=8.26·11,86²/8=145.23 кН·м.

2.5.2 Предварительное определение площади сечения продольной арматуры

Определим площадь поперечного сечения напрягаемой арматуры А_р класса S800, расположенной в растянутой зоне, методом предельных усилий (альтернативная модель).

Поперечное сечение плиты приводится к тавровой форме и в расчет вводится вся ширина полки.

Определяем ширину полки тавра.

В принятом сечении b_свеса=(2,15-0,255)/2= 0.95 м < 1/6·l_eff=1/6·11,86=1,98 м, поэтому в расчет принимаем b_свеса=0.95 м.

b_f′=0,255+2·0.95=2,15 м.

Расчетную рабочую высоту сечения d определяем с учетом толщины защитного слоя и половины диаметра арматуры (принимаем с=40 +25/2=53мм):

d=h-c=450-53 =397 мм.

Проверяем условие, определяющее положение нейтральной оси:

M_Rd= α·f_cd·b_f′·h_f′·(d-0,5·h_f′) (2.13)

M_Rd =1·20·10³·2,15·0,04·(0,397-0,5·0,04)=648,44 кН·м.

Т.к. M_sd=235,08 кН·м<M_Rd=648,44кН·м, то граница сжатой зоны проходит в полке и расчет проводится как для элементов прямоугольного сечения размерами b_f′d=2150397 мм.

Граничное значение относительной высоты сжатой зоны сечения

ξ_lim=ω/(1+σ_s,lim/ σ_s,cu (1- ω/1,1)) , (2.14)

где w — характеристика сжатой зоны бетона, определяемая

ω=k_c-0,008·α·f_cd, (2.15)

здесь k_с — коэффициент, принимаемый равным для бетона тяжелого ¾ 0,85;

ω=0,85-0,008·1·20=0,69.

s_s,lim — напряжения в арматуре, МПа, принимаемые:

s_s,lim= f_pd+400-σ_pm, (2.16)

σ_pm – величина предварительного напряжения арматуры. При подборе арматуры, когда неизвестно напряжение σ_pm, допускается его величину принимать равной 0,6·f_pd.

f_pd =640 МПа для арматуры класса S800.

s_sc,u — предельное напряжение в арматуре сжатой зоны сечения, принимаемое равным 500 МПа.

s_s,lim= 640+400-0,6·640=656 МПа.

ξ_lim=0,69/(1+656/500·(1- 0,69/1,1))=0,463

При α_m =M_sd/(α·f_cd·b·d²)=235,08/(1·20·10³·2,15·0,397²) = 0,035 относительная высота сжатой зоны

ξ=1-√1-2·α_m = 1-√1-2·0,035=0,036.

ξ=0,036< ξ _lim=0,463.

При соблюдении условия ξ ≤ ξ_lim расчетное сопротивление высокопрочной арматуры f_pd следует дополнительно умно­жать на коэффициент γ_sn=1,15 для арматуры класса S800.

η=1-0.5· ξ=1-0.5· 0.36=0.982

Требуемая площадь напрягаемой арматуры:

А_р1=M_sd/(γ_sn·f_pd•η·d), (2.17)

А_р1=235.08·10⁶/(1,15·640·0.982·397)=819.29 мм².

Принимаем 2Ø25 мм S800 (А_st=982 мм²), по одному стержню в каждом ребре.