4. Экстраполяция с помощью кубических сплайнов

Кубическая сплайн-экстраполяция представляет собой быстрый и устойчивый способ экстраполяции функций и является альтернативой полиномиальной экстраполяции. В основе экстраполяции лежит принцип разбиения заданного экстраполируемого интервала на небольшие отрезки, на каждом из которых функция задается полиномом третьей степени. Данный принцип заимствован из интерполяции сплайнами.

Основными достоинствами сплайн экстраполяции являются её устойчивость и малая трудоемкость, что позволяет получать коэффициенты кубического полинома с высокой точностью. Построение таблицы коэффициентов сплайна требует O(3) операций. Для каждой точки xi из наборов (xi, yi) входной последовательности рассчитываются параметры кубического сплайна. В процессе экстраполирования, метод находит ближайшую к точке x точку xi, в которой уже вычислены коэффициенты сплайна, и строит полином, который даёт значение искомой функции в точке x.

Кроме указанных достоинств, метод сплайновой экстраполяции имеет негативные особенности. Значение ошибки будет увеличиваться с отдалением экстраполируемой точки от заданного начального интервала в случае линейности исходной функции. Вдали от заданного интервала результаты экстраполяций отличаются, что объясняется их различными зависимостями от x.

Глава 2. Сплайн интерполяция функций

1. Приближение функции с помощью кубического сплайна

Построим интерполянту для функции  , заданной следующим образом таблица 2.1 и рис. 2.1:

X	1	2	3	4	5	6
F(x)	1.0002	1.0341	0.6	0.40105	0.1	0.23975

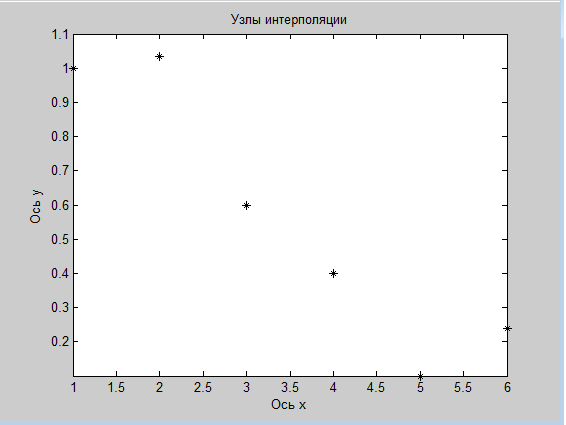
Рис. 1.

В результате интерполяции были рассчитаны следующие коэффициенты интерполянты:

Результат интерполяции(??Расписать ссылку на формулы)(Вставить формулу)

				Отрезок
1,0002	-0,140113846	0,440979231	-0,266965385
1,0341	-0,291901538	-0,359916923	0,217718462
0,6	-0,22553	0,293238462	-0,266658462
0,40105	-0,100328462	-0,506736923	0,306015385
0,1	-0,134456154	0,411309231	-0,137103077

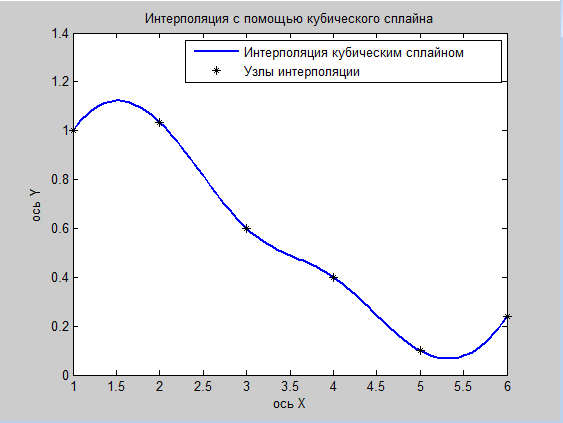
Рис. 2.

Рассмотрим  функцию  f(x)= sin(x) на отрезке [-3,3].

Интерполяция кубическими сплайнами и оценка погрешности

на [-3,3].  — сплайн-интерполяция синуса, функцию  f(x) пытаемся представить в виде некоторых элементарных функций: _, где   — фиксированный линейно независимые функции, — не определённые пока коэффициенты.

При выборе шага h = 0.25 интерполяция выглядит так:

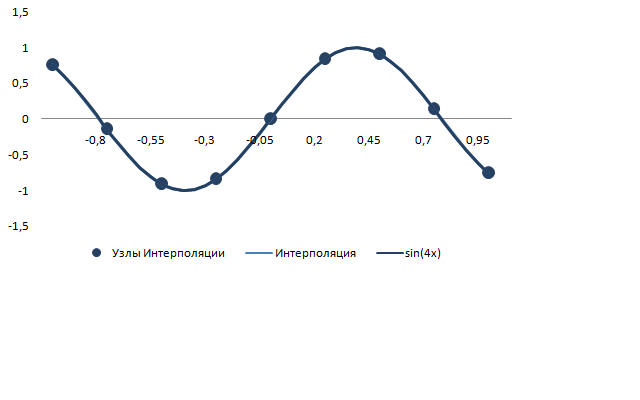
Ошибка интерполяции оценивается следующим образом [Завьялова]:

Пример: интерполяция синуса при изменении количества узлов интерполяции

Построим интерполянту функции   на отрезке , взяв равномерно отстоящие узлы с шагом 0.5 и шагом 0.25, и сравним полученные результаты.

При шаге =0,5

Ошибка интерполяции 0,429685

Оценка ошибки 3,(3)

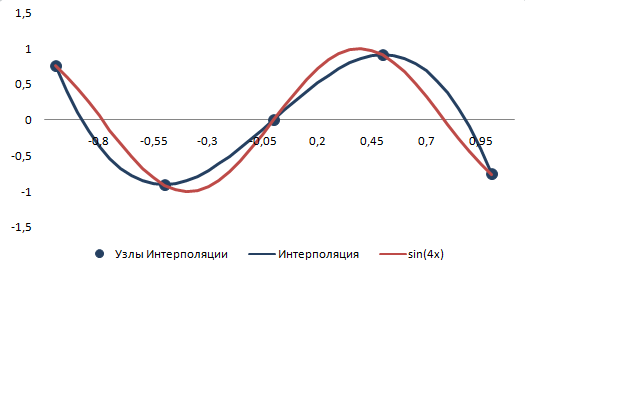
При шаге h=0,25

Ошибка интерполяции 0,005167

Оценка ошибки 0,208(3)

2. Интерполяция функций с помощью с помощью интерполяционного полинома

Используем для интерполяции точки из таблицы 1.

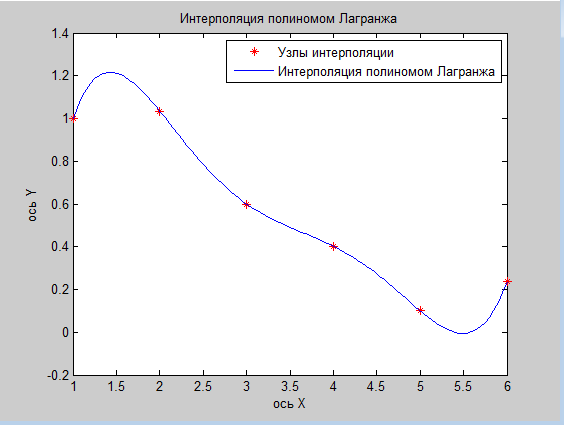
Интерполяция полиномами Лагранжа

Рассмотрим  функцию  f(x)= sin(x) на отрезке [-3,3] с шагом в 1.5. В качестве интерполирующей функции g(x) рассмотрим полином , где   - полиномы степени   вида _. 

Графики функции и приближающей её функции приведены на рис. (номер).График синуса (показан красным цветом) и интерполирующей функции (показан зелёным цветом) в этом случае выглядит так:

Рисунок (номер) – Графики функций

F(x)=sin(x) (выделить пунктиром)

Ошибка (максимальное отклонение от sin(x)): 0.1423.