3. Кубические сплайны[вержбицкий]

Пусть на задана сетка и набор ординат . Можно считать, что , где -функция определеная на .

Определение 5. Функция называется интерполяционным кубическим сплайном дефекта 1 относительно сетки , если:

1. на ,

2. 

3. 

Периодический сплайн удовлетворяет условиям

_{Так как непериодический сплайн имеет два свободных параметра, то для их определения может потребоваться выполнения либо одного из краевых условий}

_{, ;}

_{, ,}

_{либо дополнительных условий гладкости, например}

;

_{Назовём соответственно наклонами и моментами величины ,} ,

Теорема существования и единственности интерполяционного сплайна

_{Теорема} [книга]. Для любого набора существует единственный простой интерполирующий кубический сплайн, удовлетворяющий одному из условий (1)-(4)

_{Доказательство. Согласно определению кубического интерполяционного сплайна, на любом частичном , производная - линейная функция. Запишем её в виде:}

_{Интегрирую (5) по от до , имеем}

_.

_{Интегрирую (6) по от до , имеем}

_{Полагая здесь , имеем}

_,

Следовательно:

_.

_{Для получения более симметричной записи относительно индексов и представим множитель при и в виде}

_{, тогда}

_;

_.

_{Из (6) с учётом найденного значения на , имеем}

_{. (8)}

_{По определению непрерывна на . Это означает, что . Подставляя сюда значения производных согласно (8), получим}

_.

_{Приводя здесь подобные, умножая ое уравнение на , обозначим}

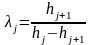_{, ; , (9)}

_{Получим}

₍₁₀₎

_{Уравнение (10) представляет собой СЛАУ относительно неизвестных ; то есть не хватает двух уравнений.}

_{Условия периодичности (1) дают , то есть число неизвестных сокращается на единицу.}

_{. Подставляя сюда значения производных, вычисленные согласно (8), получим ещё уравнение, которое формально можно включить в систему (10) считая, что индекс может принимать значение и полагая ; ; . Краевые условия (2) с учётом (8), приводят у уравнениям:}

_;

_{В случае краевых условий (3) имеем ; .}

_{Во всех трёх случаях матрицы получающихся в результате систем имеют доминирующую главную диагональ, в виду (9).}

_{При условиях (4), дифференцирования (5), имеем}

_{при из .}

_{Следовательно, условия (4) могут переписаться в виде:}

_;

_.

_{Эти уравнения нарушают доминантность главной диагонали. Выразим из них и и исключим их из системы (10). Тогда тогда первое и последнее уравнения системы перепишутся в виде:}

_{; .}

_{Получившаяся в результате система уже имеет матрицу с доминирующей главной диагональю. Таким образом, согласно утверждению 2, при выполнении любого из условий (1)-(4) величины существуют и определяются однозначно для любого набора ; тем самым по (7) однозначно определён кубический интерполяционный сплайн. Следовательно теорема доказана ???}

_{Произвол в расположении узлов сетки позволяет использовать индивидуальные свойства приближаемой функции.}

Доказательство рассмотренной теоремы даёт и способ построения простого кубического интерполяционного сплайна.(перенести)

Мб добавить свойства минимальной нормы и наилучшего приближения [Альберг]

МБ добавить раздел (¼)Оценка погрешности интерполяции.[Смотреть Завьялова]