3. Циклдық кодалау кезінде қатені табу және түзету. Циклдық коданың синдромы және онық қасиеті.

Сызықтық блокты кодтар. Басқа атауы – жүйелік кодтар. Оның ерекшелігі – екі рұқсат етілген кодтық комбинациялардың модулі 2 бойынша қосындысы соңында әрқашан рұқсат етілген кодтық комбинацияны береді. Сонымен қатар, жүйелік кодтарда ақпараттық символдар кодалау кезінде өзгермейді және ерте анықталған берілген орындарды алады. Тексеретін символдар сызықты ақпараттық символдың комбинациясы ретінде шешіледі, сондықтан олардың басқа атауы – сызықты болып табылады. Жүйелік кодтар үшін [n, k] –белгіленуі қолданылады, мұндағы k – кодтық комбинациядағы ақпараттық символдардың саны, n – кодтағы символдардың жалпы саны. Сызықтық блокты кодтарға Циклдік, Хэмминг, т.б кодтар жатады. Циклдік кодтар. Сызықтық блоктық кодтардың маңызды бір тармағы екілік циклдік кодтар (cyclic codes) болып табылады. Код кері байланысты ығыстыру регистрінде жеңі жүзеге асады; осындай кері байланысты ығыстыру регистрлерінде синдром есептелінеді; циклдік кодтың алгебралық құрылымы декодалау әдістерін табиғи түрде тиімді жүзеге асыруға мүмкіндік береді. Сонымен, егер (n, к) сызықтық кодының келесідей қасиеті болса, ол циклдікдеп аталады. Егер U= (u₀, u₁, и₂, …,u_n-1) n-кортежі S жазықтықтармағындағы кодтық сөз болса, онда циклдік ығыстыру көмегімен U-дан алынған U(1)= (u_n-1, u₀, u₁, и₂,..., u_n-₁), S-тағы кодтық сөз болып табылады. Немесе, жалпы айтқанда, i циклдік ығыстырулар арқылы алынған U(i) = (u_n-i;. u_n-i+1,…, u_n-1, u₀, u_1,… u_n-i-1), S-тағы кодтық сөз болып табылады.

Циклдік кодтарды декодалаудың бірнеше тәсілдері бар. Солардың бірі келесідегілерден тұрады: 1.Қалдықты (синдромды) есептеу. Қабылданған комбинацияны Р(Х) құраушы көпмүшесіне бөледі. R(X)=0 қалдығы комбинациялар қатесіз қабылданғанын білдіреді; 2.Қалдық салмағы W-діесептеу. Егерқалдық салмағы жөнделетін қателер санына тең немесе одан аз, яғни W≤sболса, онда қабылданған комбинациянымодуль 2 бойынша қалдықпен қосып, жөнделген комбинацияны алады; 3.Бір символға солға қарай циклдік ығысу. ЕгерW>sболса, ондасолға қарай циклдік ығысу жасап, алынған комбинацияны тағы дақұраушы көпмүшеге бөледі. Егер қалдық салмағыW≤sболса, онда циклдік ығыстырылған комбинацияны қалдықпен қосып, содан соң оны кері бір символға оңға қарай циклдік ығыстырады. Нәтижесінде жөнделген комбинация алынады; 4.Қосымша солға қарай циклдік ығысу. Егер бір символға циклдік ығысудан кейін де бұрынғыдай W>sболса, онда қосымша солға қарай циклдік ығысуларжасайды. Бұған қоса әрбір ығысқан сайынығыстырылған комбинацияны Р(Х)-ке бөліп, қалдық салмағын тексереді. W≤sболғанда 3п.-те көрсетілгендей әрекетттер орындалады, тек бір ғана өзгешелігі, қанша солға қарай ығысулар жасалса, сонша кері оңғақарай циклдік ығысулар жасалады.

Циклдықкодтың кодтаушы құрылғысының күрделілігі n код ұзындығына пропорционал болуы керек. Циклдық кодердің жоғарғы қиындық шекарасы ϗц≤5Rn. Қателерді түзетумен декодалау кезінде циклдық кодердің күрделілігі сызықты декодерге қарағанда ықшамдауға болады. Біріншіден, қабылданған тізбектің тексеруші матрицаға көбейтіндісі оны туынды көпмүшеге бөлуімен алмастырылады, екіншіден сақталынатын синдромдар мен қателер көпмүшелері азайады, себебі олардың кейбірі типтік синдромнан немесе қателер көпмүшесінен циклдық жылжу арқылы алынуы мүмкін. Әртүрлі циклдық жылжулардың саны код ұзындығынан аспайтындықтан, типтік синдромдарды қолдану n-нан аспайтын ұтыс алуға мүмкіндік береді. Сондықтан циклдық кодтардың синдромдық декодалау құрылғыларының күрделілігі код ұзындығына байланысты ϗ≤2^n(1-R) көрсеткіштік сипаттамасын сақтайды.

Циклдық код синдромы.Мысалы, m(x)=1+x²+x³+x⁷+x⁹=1011000101, g(x)=1+x²+x⁴+x⁵=101011, онда x^n-k=x⁵ және х^n-km(x)=x⁵+x⁷+x⁸+x¹²+x¹⁴=000001011000101.

х^n-km(x)-ты g(x)-ке бөлу. Нәтижесінде q(x)=110101011 және r=01110 .

кодтық көпмүше х^n-km(x)+r(x)=x+x²+x³+x⁵+x⁷+x⁸+x¹²+x¹⁴=01110 тексеруші разрядтар 1011000101- ақпараттық разрядтар. Қателр көпмүшелігі е(х) = 1101011 болса, онда р(х)=101000111000101. Егер p(x)ты g(x)=101011 ке бөлсек, онда қалдық s(x)=1 болады., яғни осыдан қабылданған кодтық комбинацияда қате бар деген сөз. Қалдық s(x) синдpом деп аталады. s(x)=p(x)+ g(x)l(x) болғандықтан, ал р(х)=f(x)+e(x), онда е(х)=[l(x)+q(x)]g(x)+s(x), яғни синдром s(x) қателер көпмүшелігі e(x)- ты g(x)-ке бөлгендегі қалдыққа тең. Егер синдром нөлге тең болса, декодер дұрыс қабылдау жайлы шешім қабылдайды. Қателерді табудың және дұрыстаудың негізгі принциптері

Қателерден қорғау үшін өтімділікті қолданудың екі негізгі тәсілін қарастырайық. Бірінші тәсілде қатені табу және қате болуының тексеру үшін қайта жіберу жұптық бақылау биті қолданылады. Бірқ қбылдау құрылғысы қатені түзету үшін ешқандай әрекет жасамайды, ол тек қана таратқышқа мәліметтерді қайта жіберуге сұраныс жасайды. Осындай таратқыш және қабылдағыш арасындағы диалог үшін екі жақты байланыс қажет. Екінші тәсіл, тура түзету, бұл тек қана бір жақты байланыс желісін қажет етеді. Өйткені бұл жағдайда жұптық бақылау биті қателерді табу үшін де, оларды түзету үшін де қызмет етеді. Ары қарай біз барлық қателер комбинациясын түзетуге болмайтынын көреміз. Сондықтан түзету кодтары қателерді дұрыстау мүмкіндіктеріне байланысты жіктеледі. Қателерді кодтар арқылы табу және түзету принципі геометриялық модельдердің көмегімен суреттеледі. Кез келген nэлементті екілік кодты n бірқалыпты куб ретінде қарастыруға болады. Онда әрбір шың кодалық комбинацияны көрсетеді, ал куб қабырғасының ұзындығы бір бірлікке сай келеді,бұндай кубта шыңдар арасының қашықтығы олардың арасында орналасқан қабырғаларының минималды мәнімен есептеледі, ол d болып белгіленеді және кодалық қашықтық деп аталады.

Емтихан билеті №23

1. Аддитивті және мультипликтивті оралғылар және олардың қажетті сигналдарға әсерлігі. Кез келген арнамен жіберілген сигналдағы бір жалпы қиыншылық - аддитивті шу. Жалпы айтқанда, аддитивті шу көбінесе байланыс жүйесінде қолданылатын әртүрлі резистр және қатты денелі құрылғылар электрлік компоненттер ішінде пайда болады. Осы шуылдарды көбінесе жылулық шуылдар деп атайды. Басқа шу көзідері және интерференция жүйе сыртында да пайда бола алады, мысалы, басқа арна қолданушылардың ауыспалы бөгеттері. Аддитивті шуылы бар арна. Байланыс арнасы үшін ең қарапайым математикалық модель- бұл 3.1 суретте көрсетілген аддитивті шуылы бар арна. Бұл модельде s(t) жіберілетін сигналы n(t) аддитивті шуылды процессінің ықпалына ғана тәуелді. Аддитивті шуыл физикалық түрде бөтен электрлі бөгеуілдерден, байланыс жүйесінің қабылдағышындағы электронды компоненттерінен және күшейткіштерінен және де сигналдардың интерференциясынан пайда болуы мүмкін.

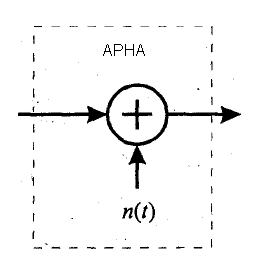
3.1- сурет. Аддитивті шуылы бар арна

Егерде шуыл негізінде қабылдағыштағы электронды компоненттермен және күшейткіштермен көрсетілген болса, оны жылулық шуыл ретінде суреттеуге болады. Шуылдың бұл түрі статистикалық түрде гаусстық шуылды процесс оңай математикалық интерпретациясы бар болғаннан кейін,ол байланыс жүйесінің анализі және синтезі кезінде арнаның күштірек моделі болып табылады. Арналардың өшулігі оңай модельге қосылады. Арна арқылы өту кезінде сигнал әлсіресе, онда қабылданатын сигнал

r(t)=αs(t)+n(t) (3.1) мұндағы α- сызықты арналы сүзгінің өшу коэффициенті.