
Задание №4
В таблице представлена динамика объема выпускаемой продукции по предприятию за 1997-2006гг:
Годы |
1997 |
1998 |
1999 |
2000 |
2001 |
2002 |
2003 |
2004 |
2005 |
2006 |
Объем продукции, тыс. шт. |
1190 |
1263 |
1523 |
1600 |
1630 |
1720 |
1888 |
1922 |
2008 |
2200 |
Вычислить аналитические показатели динамики: абсолютные приросты (цепные и базисные), темпы роста (цепные и базисные), темпы прироста (цепные и базисные), абсолютное значение 1% прироста, относительное ускорение (коэффициент опережения).
Вычислить средний уровень ряда, средний абсолютный прирост, средний темп роста.
Спрогнозировать значение объема производства на 2007г. на основе средних показателей динамики.
Проверить, является ли ряд стационарным. Если да, то спрогнозировать объем производства на 2007г. на основе стационарного ряда. В противном случае подобрать уравнение тренда и спрогнозировать объем производства на 2007г. на основе экстраполяции тренда. Вычислить остаточную дисперсию.
Решение:
1) Определим аналитические показатели динамики (цепные и базисные).
а) абсолютные приросты.
базисные цепные
![]()
![]()
б) темпы роста.
базисные цепные
![]()
![]()
в) темпы прироста.
базисные цепные
![]()
![]()
г) абсолютное значение 1% прироста.
![]()
Расчет показателей приведем в табл. 4.1.
Таблица 4.1
Динамика объема выпускаемой продукции по предприятию за 1997-2006гг.
Год |
Объем, тыс. шт. |
Абсолютные приросты, тыс. шт. |
Темпы роста, % |
Темпы прироста, % |
Абсолютное значение 1% прироста, тыс. шт. |
Коэффициент опережения |
|||
базисные
|
цепные
|
базисные
|
цепные
|
базисные
|
цепные
|
||||
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
1997 |
1190 |
– |
– |
– |
– |
– |
– |
– |
– |
1998 |
1263 |
73 |
73 |
106,1 |
106,1 |
6,1 |
6,1 |
11,90 |
– |
1999 |
1523 |
333 |
260 |
128,0 |
120,6 |
28,0 |
20,6 |
12,63 |
1,14 |
2000 |
1600 |
410 |
77 |
134,5 |
105,1 |
34,5 |
5,1 |
15,23 |
0,87 |
2001 |
1630 |
440 |
30 |
137,0 |
101,9 |
37,0 |
1,9 |
16,00 |
0,97 |
2002 |
1720 |
530 |
90 |
144,5 |
105,5 |
44,5 |
5,5 |
16,30 |
1,04 |
2003 |
1888 |
698 |
168 |
158,7 |
109,8 |
58,7 |
9,8 |
17,20 |
1,04 |
2004 |
1922 |
732 |
34 |
161,5 |
101,8 |
61,5 |
1,8 |
18,88 |
0,93 |
2005 |
2008 |
818 |
86 |
168,7 |
104,5 |
68,7 |
4,5 |
19,22 |
1,03 |
2006 |
2200 |
1010 |
192 |
184,9 |
109,6 |
84,9 |
9,6 |
20,08 |
1,05 |
За период 1997-2006гг. объем выпускаемой предприятием продукции увеличился на 84,9% или на 1010 тыс. шт.
2) Определим:
а) средний уровень ряда динамики.

![]() = 1694,4 тыс. шт.
= 1694,4 тыс. шт.
Среднегодовой объем выпуска продукции по предприятию за период 1997-2006гг. составит 1694,4 тыс. шт.
б) среднегодовой абсолютный прирост.
![]()
![]() = 112,2 тыс. шт.
= 112,2 тыс. шт.
В среднем ежегодно выпуск продукции по предприятию увеличивался на 112,2 тыс.шт.
в) среднегодовой темп роста.

![]() = 107,1%
= 107,1%
В среднем ежегодно объем выпуска продукции за период 1997-2006 гг. составлял 107,1% к уровню предыдущего года.
3) Спрогнозируем объем производства на 2007 год с помощью:
а) среднегодового абсолютного прироста.
2200 + 112,2 = 2312,2 тыс. шт.
б) среднегодового темпа роста.
2200∙1,071 = 2356,2тыс. шт.
4) Проверим ряд динамики на наличие тренда методом существенности разности средних.
Разобьем временной ряд на 2 равные части:
t |
1 |
2 |
3 |
4 |
5 |
|
1190 |
1263 |
1523 |
1600 |
1630 |
t |
6 |
7 |
8 |
9 |
10 |
|
1720 |
1888 |
1922 |
2008 |
2200 |
По каждой части определим среднюю и исправленную дисперсию.




Проверим гипотезу о равенстве дисперсий с помощью F-критерия Фишера при уровне значимости 0,05.

![]()
![]() (0,05; 4; 4) = 6,39
(0,05; 4; 4) = 6,39
Т.к., F < , то с вероятностью 0,95 дисперсии однородны.
Проверим гипотезу об отсутствии тренда с помощью t-критерия Стьюдента при уровне значимости 0,05.
![]()

 = 119,54
= 119,54
![]() = 4,24
= 4,24
(0,05; 8) = 2,31
Так как < t, то гипотезу об отсутствии тренда отвергаем. Другими словами данный ряд динамики не является стационарным.
Подберем уравнение тренда.
Построим график данного временного ряда.
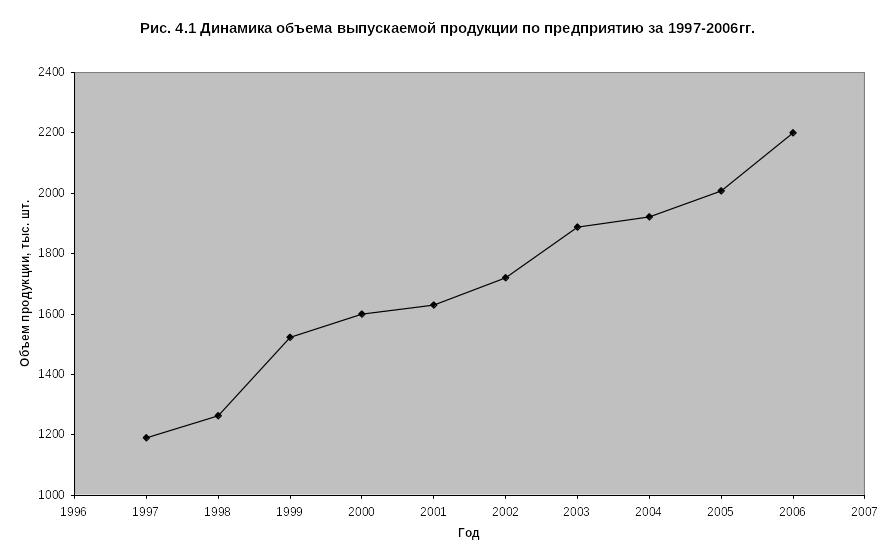
Исходя из графика, можно предположить, о присутствии линейного тренда во временном ряду.
Найдем параметры уравнения:
= a + bt,
где a и b найдем из системы нормальных уравнений:

Промежуточные расчеты представим в табл. 4.2.
Таблица 4.2
Промежуточные расчеты
Год |
Объем, тыс. шт. у |
t |
|
yt |
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
1997 |
1190 |
1 |
1 |
1190 |
1223,8 |
1145 |
1998 |
1263 |
2 |
4 |
2526 |
1328,4 |
4278 |
1999 |
1523 |
3 |
9 |
4569 |
1433,0 |
8104 |
2000 |
1600 |
4 |
16 |
6400 |
1537,5 |
3901 |
2001 |
1630 |
5 |
25 |
8150 |
1642,1 |
147 |
2002 |
1720 |
6 |
36 |
10320 |
1746,7 |
712 |
2003 |
1888 |
7 |
49 |
13216 |
1851,3 |
1350 |
2004 |
1922 |
8 |
64 |
15376 |
1955,8 |
1144 |
2005 |
2008 |
9 |
81 |
18072 |
2060,4 |
2745 |
2006 |
2200 |
10 |
100 |
22000 |
2165,0 |
1228 |
Итого |
16944 |
55 |
385 |
101819 |
16944 |
24754 |
![]()
![]()
Отсюда уравнение имеет вид:
= 1119,3 + 104,6t
Построим прогноз объема производства на 2007 год на основе экстраполяции тренда.
(11)= 1119,3 + 104,6∙11 = 2269,9 тыс. шт.
Определим остаточную дисперсию.
![]()
![]() 3094,25
3094,25
