Задание №2
В табл. 2.1 приведены данные о величине уставного капитала для 100 малых и средних коммерческих банков по региону (млрд. руб.):
Таблица 2.1
25,6 |
72,8 |
11,0 |
67,2 |
69,6 |
87,7 |
38,7 |
63,8 |
1,2 |
92,6 |
8,5 |
94,3 |
43,6 |
56,7 |
9,1 |
93,2 |
92,0 |
49,4 |
27,8 |
71,9 |
59,1 |
85,6 |
70,5 |
91,6 |
82,0 |
78,4 |
18,5 |
14,4 |
19,8 |
47,1 |
63,0 |
42,5 |
97,1 |
54,4 |
83,7 |
84,1 |
74,0 |
70,6 |
65,7 |
4,1 |
44,3 |
89,6 |
70,6 |
47,2 |
95,7 |
43,1 |
3,4 |
43,9 |
82,8 |
88,5 |
43,9 |
35,7 |
95,6 |
67,4 |
34,3 |
79,1 |
26,2 |
58,6 |
38,7 |
16,5 |
64,1 |
75,3 |
19,6 |
23,0 |
75,6 |
77,1 |
95,6 |
65,9 |
45,1 |
98,4 |
74,4 |
38,3 |
84,8 |
14,4 |
77,4 |
50,9 |
41,6 |
94,0 |
98,9 |
96,0 |
55,7 |
13,4 |
66,0 |
16,2 |
51,8 |
27,7 |
92,1 |
41,1 |
65,6 |
25,5 |
41,4 |
77,8 |
37,4 |
12,8 |
45,6 |
64,0 |
25,7 |
2,4 |
41,4 |
23,0 |
Построить интервальный вариационный ряд. Построить гистограмму и кумуляту. Вычислить числовые характеристики вариационного ряда (среднее значение, моду, медиану, дисперсию, среднее квадратическое отклонение, асимметрию и эксцесс). Проверить коэффициенты асимметрии и эксцесса на значимость.
Решение:
1) Построим интервальный вариационный ряд.
Определим длину интервала:
n = 1 + 3,322∙lgN
n = 1 + 3,322∙lg100 = 8
= 12,2 млрд. руб.
Таблица 2.2
Раcпределение коммерческих банков региона по величине уставного капитала
Группы по величине уставного капитала, млрд. руб. |
Число банков |
Накопленные частоты |
1 |
2 |
3 |
1,2 – 13,4 |
8 |
8 |
13,4 – 25,6 |
11 |
19 |
25,6 – 37,8 |
8 |
27 |
37,8 – 50,0 |
18 |
45 |
50,0 – 62,2 |
7 |
52 |
62,2 – 74,4 |
17 |
69 |
74,4 – 86,6 |
14 |
83 |
86,6 – 98,9 |
17 |
100 |
Итого |
100 |
– |
2) Построим графики полученного ряда распределения.
а) гистограмма распределения.
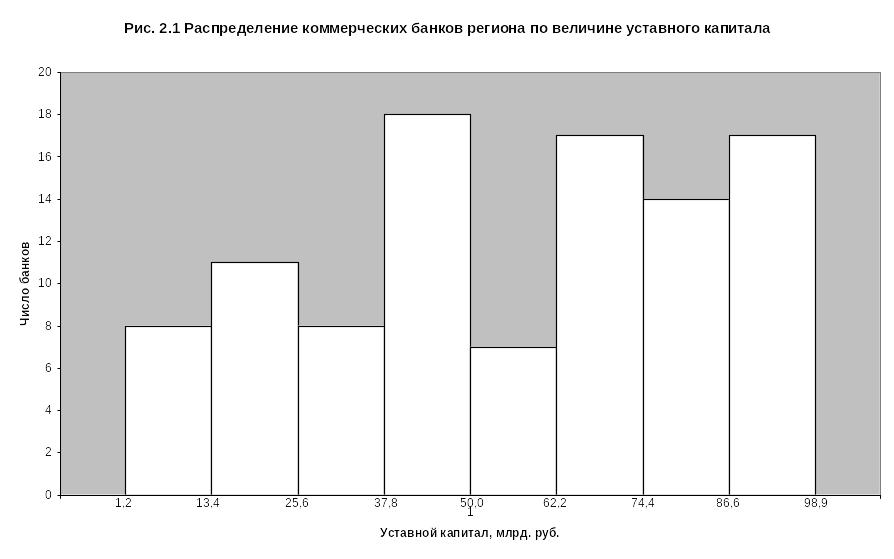
б) кумулята распределения.
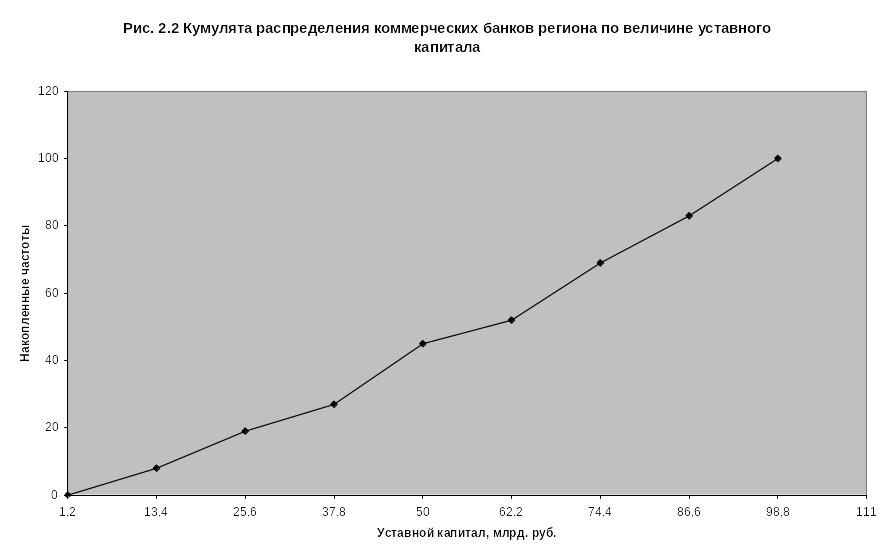
3) Вычислим числовые характеристики вариационного ряда.
а) среднее значение.
Промежуточные расчеты представим в табл. 2.3.
Таблица 2.3
Промежуточные расчеты
Группы по величине уставного капитала, млрд. руб. |
Число банков
|
Расчетные показатели |
||||
|
|
|
|
|
||
1 |
2 |
3 |
4 |
5 |
6 |
7 |
1,2 – 13,4 |
8 |
7,3 |
58,4 |
18767 |
-908952 |
44024186 |
13,4 – 25,6 |
11 |
19,5 |
214,5 |
14442 |
-523289 |
18960850 |
25,6 – 37,8 |
8 |
31,7 |
253,6 |
4621 |
-111063 |
2669281 |
37,8 – 50,0 |
18 |
43,9 |
790,2 |
2521 |
-29831 |
353020 |
50,0 – 62,2 |
7 |
56,1 |
392,7 |
1 |
0 |
0 |
62,2 – 74,4 |
17 |
68,3 |
1161,1 |
2684 |
33732 |
423874 |
74,4 – 86,6 |
14 |
80,5 |
1127 |
8587 |
212665 |
5266857 |
86,6 – 98,9 |
17 |
92,7 |
1575,9 |
23230 |
858729 |
31743789 |
Итого |
100 |
– |
5573,4 |
74853 |
-468008 |
103441856 |
= 55,7 млрд. руб.
Средний размер уставного капитала коммерческих банков в регионе составит 55,7 млрд. руб.
б) дисперсия.
= 748,53 млрд.
в) среднее квадратическое отклонение.
27,4
млрд. руб.
Таким образом, средняя величина колеблемости уставного капитала коммерческих банков по среднему квадратическому отклонению составит 27,4 млрд. руб.
г) мода.
= 43,6 млрд. руб.
Таким образом, в регионе преобладают коммерческие банки с величиной уставного капитала 43,6 млрд. руб.
д) медиана.
Ме =
Ме =
= 58,7 млрд. руб.
В регионе 50% коммерческих банков имеют величину уставного капитала менее 58,7 млрд. руб., а 50% коммерческих банков – более 58,7 млрд. руб.
е) асимметрия.
= –
4680,08
=
– 0,23
Оценим значимость асимметрии.
= 0,24
= 0,96
< 3
Асимметрия не существенна.
ж) эксцесс.
=
1034418,56
=
– 1,16
Оценим значимость эксцесса.
= 0,46
= 2,52
< 3
Эксцесс не существенен.