3. Проверить модель на адекватность и определить её точность.

Исследуем модель на адекватность и точность, для этого должны выполняться:

t	y(t)	e(t)	Точки пов-та	e2	e(t)-e(t-1)	(e(t) -e(t-1))2	[e(t)]:y(t)·100
1	30	1,20		1,44	-3,99	15,97	4,01
2	28	-2,79	1	7,80	2,00	4,02	9,97
3	33	-0,79	1	0,61	2,00	4,01	2,38
4	37	1,21	0	1,47	0	3,13	3,28
5	40	1,22	1	1,49	-0,99	0,98	3,05
6	42	0,22	0	0,05	0	1,39	0,54
7	44	0,23	0	0,05	2,00	4,02	0,52
8	49	2,23	1	5,00	-4,99	24,94	4,56
9	47	-2,76	0	7,60	2,75	7,60	5,86
Ʃ	350	0	4	25,55	-1,20	61,56	34,21

а) Математическое ожидание уровней рядов остатков должно стремиться к нулю.

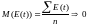где n – иcследуемый период.

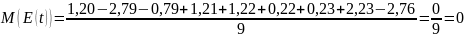
б) Уровни ряда остатков 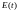должны быть случайными числами, это проверяется с помощью критерия поворотных точек. По этому критерию каждый уровень ряда остатков сравнивается с 2-мя соседними уровнями. Если он больше или меньше обоих ему соответствует точка поворота. Например, во втором ряду значение (-2,79) сравнивается с двумя соседними, это (1,20) в первом ряду и (-0,79) в третьем ряду, (1,20) > (-2,79), (-2,79) < (-0,79),значит, точка поворота имеется. В 5 ряду значение (1,22) сравнивается с двумя с соседними ((1,22) >(1,21), (1,22) > (0,22)), точка поворота отсутствует.

В случайном ряду чисел число точек поворота, N – количество чисел проверяемых в работе. В нашем случае N=9 p > 2, р = 4 > 2. Следовательно, наши ошибки случайны.

в) должны быть независимы (отсутствие автокорреляции). Проверяется с помощью критерия Дарбина –Уотсона.

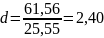
Полученное значение сравнивается с двумя табличными d₁ и d₂. Для N=9 и 5% уровня значимости по таблице Дарбина – Уотсона d₁ = 1.08, а d₂ = 1,36. В нашем случае 2,40 > 1,36, а это значит что d > d₂, поэтому у нас уровни будут независимы.

г) Точность модели мы сможем определить с помощью средней относительной ошибки.

Найдём её по формуле: ;

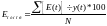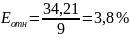
У нас относительная ошибка входит в интервал между 5% и 15%, значит, точность хорошая.

4. Найдём коэффициент эластичности и детерминации.

а) Коэффициент эластичности характеризует, на сколько процентов изменится значение y при изменении x на 1%. Он находится по формуле: ;

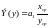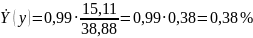
Вывод: при изменении x на 1%, y изменится на 0,38%.

б) Коэффициент детерминации показывает долю вариации признака под влиянием факторов, включённых в модель. Коэффициент детерминации найдём по формуле:

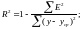
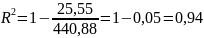
Вывод: Коэффициент детерминации R² = 0,94, значит, уравнением регрессии объясняется 87% дисперсии результативного признака, а на долю прочих факторов приходится 67% ее дисперсии (т.е. остаточная дисперсия). Величина коэффициента детерминации служит важным критерием оценки качества линейных и нелинейных моделей. Чем значительнее доля объясненной вариации, тем меньше роль прочих факторов, и значит, модель регрессии хорошо приближает исходные данные и такой регрессионной моделью можно воспользоваться для прогноза значений результативного показателя.