Ноу впо "Балтийский институт экономики и финансов" (биэф) Факультет финансов, учета и управления
-
Специальность:
«Бухгалтерский учет, анализ и аудит»
РАБОТА
По дисциплине: Эконометрика_____________________________
Тема: Лабораторная работа. Вариант 4._______________________
-
Выполнил:
Студент (ка) IIкурса,
Группы №__3205__
Фамилия И.О._____
_Шевченко Т.М.__
Проверил:
Фамилия преподавателя
_Жарикова Л.А.___
г. Калининград, 2014 г.
Лабораторная работа.
Вариант 4.
Дано:
у |
30 |
28 |
33 |
37 |
40 |
42 |
44 |
49 |
47 |
х1 |
5 |
7 |
10 |
12 |
15 |
18 |
20 |
23 |
26 |
х2 |
12 |
15 |
16 |
19 |
17 |
20 |
24 |
25 |
28 |
X
Требуется:
1) Найти коэффициенты корреляции Rx1y и Rx2y и по их значениям выбрать ведущий фактор.
2) Построить линейную однопараметрическую модель регрессии для выбранного фактора.
3) Проверить модель на адекватность и определить её точность.
4) Найти коэффициент эластичности и детерминации, сделать вывод.
5) Построить точечный и интервальный прогноз по модели регрессии на 2 шага вперёд.
6) Отобразить на графике реальные данные результатов расчётов и прогнозирования.
1. Найдём коэффициенты парной корреляции Rx1y и Rx2y и по их значениям выберем ведущий фактор.
а). Найдём коэффициент парной корреляции для Rx1y.
t |
y(t) |
x(t) |
(x-xср) |
(x-xср)2 |
y-yср |
(y-yср)2 |
(x-xср) ·(y-yср) |
1 |
30 |
5 |
-10,11 |
102,23 |
-8,88 |
79,01 |
89,87 |
2 |
28 |
7 |
-8,11 |
65,79 |
-10,88 |
118,56 |
88,32 |
3 |
33 |
10 |
-5,11 |
26,12 |
-5,88 |
34,67 |
30,09 |
4 |
37 |
12 |
-3,11 |
9,67 |
-1,88 |
3,56 |
5,87 |
5 |
40 |
15 |
-0,11 |
0,01 |
1,11 |
1,23 |
-0,12 |
6 |
42 |
18 |
2,88 |
8,34 |
3,11 |
9,67 |
8,98 |
7 |
44 |
20 |
4,88 |
23,90 |
5,11 |
26,12 |
24,98 |
8 |
49 |
23 |
7,88 |
62,23 |
10,11 |
102,23 |
79,76 |
9 |
47 |
26 |
10,88 |
118,56 |
8,11 |
65,79 |
88,32 |
Ʃ |
350 |
136 |
0,00 |
416,88 |
0,00 |
440,88 |
416,11 |
Коэффициенты
парной корреляции Rx1y
найдём по формуле: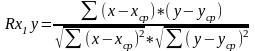
Где: xcp = 136 : 9 = 15,11
ycp = 350 : 9 = 38,88
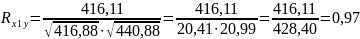
Ответ: Коэффициент парной корреляции для Rx1y.= 0,97.
б) Найдём коэффициент парной корреляции для Rx2y.
-
t
y(t)
x(t)
(x-xср)
(x-xср)2
(y-yср)
(y-yср)2
(x-xср)·(y-yср)
1
30
12
-7,55
57,08
-8,88
79,01
67,16
2
28
15
-4,55
20,75
-10,88
118,56
49,60
3
33
16
-3,55
12,64
-5,88
34,67
20,93
4
37
19
-0,55
0,30
-1,88
3,56
1,049
5
40
17
-2,55
6,53
1,11
1,23
-2,83
6
42
20
0,44
0,19
3,11
9,67
1,38
7
44
24
4,44
19,75
5,11
26,12
22,71
8
49
25
5,44
29,64
10,11
102,23
55,049
9
47
28
8,44
71,30
8,11
65,79
68,49
Ʃ
350
176
0,00
218,22
0,00
440,88
283,55
Коэффициенты парной корреляции Rx2y найдём по формуле:
;
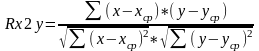Где: xcp2 = 176 : 9 = 19,55
ycp2 = 350 : 9 = 38,88
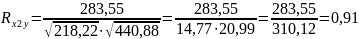
Ответ: Коэффициент парной корреляции для Rx2y.= 0,91.
Из двух полученных факторов выбираем тот, который наиболее тесно связан с зависимой переменной. Ему соответствует наибольший по модулю коэффициент корреляции.
Rx1y > Rx2y [0,97] > [0,91].
Из двух полученных факторов, ведущим является фактор №1, т.к ему соответствует наибольший по модулю коэффициент корреляции.