1. Рассчитывают и заполняют начальную симплекс-таблицу с допустимым единичным базисом, включая индексную строку.

2. В качестве направляющего столбца выбирают Aj, для которого

 .

3. Направляющая строка Aі выбирают из условия

4. Делают один шаг (итерацию) метода полного исключения Гаусса с направляющим элементом a_ij, для чего используют соотношения (2.2.16) - (2.2.18). В частности, элементы индексной строки новой таблицы вычисляют в соответствии с формулой

    l=1,2, ..., n.

Правильность вычислений контролируют по формулам непосредственного счета:

                             (2.2.23)

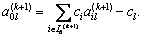                             (2.2.24)

В столбце B_x новой таблицы заменяют x_i на x_j, а в столбце С c_i на c_j.

5. Если все a_0l^(k+1)0, l=1,…,n, то новое базисное решение x_i= a_i0^(k+1), iI_б^(k+1) – оптимально. В противном случае переходят к этапу 2 и выполняют очередную итерацию.

6. Второй, третий и четвертый этапы повторяют до тех пор, пока одна из итераций не закончится одним из двух исходов:

а) все a_0l 0. Это признак (критерий) оптимальности базисного решения последней симплекс-таблицы;

б) найдется такой a_0j=_j<0, что все элементы этого столбца a_rj0,   r = 1, …, m. Это признак неограниченности целевой функции z= c_jx_j на множестве допустимых решений задачи.

Назовем некоторые особенности применения табличного симплекс-метода.

Если в качестве начального базиса выбирают базис из свободных переменных, для которых c_i=0, то оценки для всех небазисных переменных равны _j = a_0j = –c_j, а соответствующее значение целевой функции

a₀₀= c_ix_i=0, iI_б.

Отсутствие векторов с отрицательными оценками при решении задач максимизации является признаком оптимальности соответствующего базисного решения.

Если существует такой небазисный вектор, для которого оценка отрицательна, а все элементы этого столбца неположительны, то целевая функция задачи в области допустимых решений неограничена.

При решении задач минимизации в базис вводится вектор с наибольшей положительной оценкой, а отсутствие таких векторов является признаком оптимальности последнего базисного решения.

Пример 2.4.

          Максимизировать  4x₁+3x₂

при ограничениях

x₁  4000;

x₂  6000;

x₁ + x₂  6000;

x₁, x₂  0.

Расширенная форма задачи имеет такой вид:

        максимизировать 4x₁+3x₂

при ограничениях

1x₁ + 0x₂ + 1x₃ + 0x₄ + 0x₅ = 4000;

0x₁ + 1x₂ + 0x₃ + 1x₄ + 0x₅ = 6000;

1x₁ + 2/3x₂ + 0x₃ + 0x₄ + 1x₅ = 6000;

Так как A₀>0, а векторы A₃, A₄, A₅ образуют единичный базис, то задачу можно решать методом симплекс-таблиц.

Первая итерация. Составляем и заполняем начальную симплекс-таблицу (табл.2.3).

Таблица 2.3.

Ci			4	3	0	0	0
	Bx	Ai0	A1	A2	A3	A4	A5
0	X3	4000	1	0	1	0	0
0	X4	6000	0	1	0	1	0
0	X5	6000	1	1/3	0	0	1
		0	-4	-3	0	0	0

Поскольку –4<–3<0, то направляющий столбец – первый.

Составив отношение вида ,определим направляющую строку.Для этого находим

 .

Итак, направляющая строка -первая, направляющий элемент a₁₁=1.

Выполнив первую итерацию симплекс-метода, получим табл. 2.4.

Таблица 2.4.

Ci			4	3	0	0	0
	Bx	ai0	A1	A2	A3	A4	A5
4	X1	4000	1	0	1	0	0
0	X4	6000	0	1	0	1	0
0	X5	2000	0	2/3	-1	0	1
		160000	0	-3	4	0	0

Вторая итерация. Как видим с табл. 2.4.,направляющий столбец – второй, а направляющая строка – третья, так как

Выполнив очередную итерацию симплекс-метода, получим симплекс-таблицу 2.5.

Таблица 2.5.

Ci			4	3	0	0	0
	Bx	ai0	A1	A2	A3	A4	A5
4	X1	4000	1	0	1	0	0
0	X4	3000	0	0	3/2	1	-3/2
3	X2	3000	0	1	-3/2	0	3/2
		250000	0	0	-1/2	0	9/2

Третья итерация. Так как a₀₃= -1/2 <0, то направляющий столбец A₃, а направляющая строка – вторая, поскольку a₂₃=3/2. Выполнив очередную итерацию с направляющим элементом a₂₃=3/2, получим симплекс-таблицу 2.6.

Таблица 2.6.

Ci			4	3	0	0	0
	Bx	ai0	A1	A2	A3	A4	A5
4	X1	2000	1	0	0	-2/3	1
0	X3	2000	0	0	1	2/3	-1
3	X2	6000	0	1	0	1	0
		260000	0	0	0	1/3	4

Поскольку в индексной строке табл. 2.6. все оценки положительны, то найдено оптимальное решение: x_1опт=2000, x_2опт=6000, x_3опт=2000.

Соответствующее значение целевой функции:

max (4x₁+3x₂)=a₀₀=26000=4x_1опт+3x_2опт.

Транспортная задача. Различные технико-экономические и экономические задачи менеджмента, от оптимальной загрузки станка и раскройки стального листа или полотна ткани до анализа межотраслевого баланса и оценки темпов роста экономики страны в целом, приводят к необходимости решения тех или иных задач линейного программирования. В книге [1] приведен обширный перечень публикаций, посвященный многочисленным применениям линейного программирования в металлургии, угольной, химической, нефтяной, бумажной и прочих отраслях промышленности, в проблемах транспорта и связи, планирования производства, конструирования и хранения продукции, сельском хозяйстве, в научных исследованиях, в том числе экономических, и даже при регулировании уличного движения.

 В качестве очередного примера рассмотрим т.н. транспортную задачу. Имеются склады, запасы на которых известны. Известны потребители и объемы их потребностей. Необходимо доставить товар со складов потребителям. Можно по-разному организовать "прикрепление" потребителей к складам, т.е. установить, с какого склада какому потребителю и сколько вести. Кроме того, известна стоимость доставки единицы товара с определенного склада определенному потребителю. Требуется минимизировать издержки по перевозке.

 Например, может идти речь о перевозке песка - сырья для производства кирпичей. В Москву песок обычно доставляется самым дешевым транспортом - водным. Поэтому в качестве складов можно рассматривать порты, а в качестве запасов - их суточную пропускную способность. Потребителями являются кирпичные заводы, а их потребности определяются суточным производством (в соответствии с имеющимися заказами). Для доставки необходимо загрузить автотранспорт, проехать по определенному маршруту и разгрузить его. Стоимость этих операций рассчитывается по известным правилам, на которых не имеет смысла останавливаться. Поэтому затраты на доставку товара с определенного склада тому или иному потребителю можно считать известными.

 Рассмотрим пример транспортной задачи, исходные данные к которой представлены в табл. 3. В ней, кроме объемов потребностей и величин запасов, приведены стоимости доставки единицы товара со склада i, i = 1,2,3, потребителю j, j = 1,2,3,4. Например, самая дешевая доставка - со склада 2 потребителям 1 и 3, а также со склада 3 потребителю 2. Однако на складе 2 имеется 80 единиц товара, а потребителям 1 и 3 требуется 50+70 =120 единиц, поэтому к ним придется вести товар и с других складов. Обратите внимание, что в табл.3 запасы на складах равны суммарным потребностям. Для примера с доставкой песка кирпичным заводам это вполне естественное ограничение - при невыполнении такого ограничения либо порты будут засыпаны горами песка, либо кирпичные заводы не выполнят заказы.

Таблица 3.

Исходные данные к транспортной задаче.

	Потреби-тель 1	Потреби-тель 2	Потреби-тель 3	Потреби-тель 4	Запасы на складах
Склад 1	2	5	5	5	60
Склад 2	1	2	1	4	80
Склад 3	3	1	5	2	60
Потреб-ности	50	40	70	40	200

Надо спланировать перевозки, т.е. выбрать объемы Х_ij  поставок товара со склада i потребителю j , где i = 1,2,3; j = 1,2,3,4. Таким образом, всего в задаче имеется 12 переменных. Они удовлетворяют двум группам ограничений. Во-первых, заданы запасы на складах:

X₁₁  + Х₁₂  + Х₁₃  + Х₁₄  = 60 ,

X₂₁  + Х₂₂  + Х₂₃  + Х₂₄  = 80 ,

X₃₁  + Х₃₂  + Х₃₃  + Х₃₄  = 60 .

Во-вторых, известны потребности клиентов:

X₁₁  + Х₂₁ + Х₃₁   = 50 ,

X₁₂  + Х₂₂ + Х₃₂  = 40 ,

X₁₃  + Х₂₃ + Х₃₃   = 70 ,

X₁₄  + Х₂₄ + Х₃₄   = 40 .

Итак, всего 7 ограничений типа равенств. Кроме того, все переменные неотрицательны - еще 12 ограничений.

 Целевая функция - издержки по перевозке, которые необходимо минимизировать:

F = 2 X₁₁  + 5 Х₁₂  + 4 Х₁₃  + 5 Х₁₄  + X₂₁  + 2 Х₂₂  + Х₂₃  + 4 Х₂₄  +

+ +3 X₃₁  + Х₃₂  + 5 Х₃₃   + 2 Х₃₄  → min .

 Кроме обсуждаемой, рассматриваются также различные иные варианты транспортной задачи. Например, если доставка производится вагонами, то объемы поставок должны быть кратны вместимости вагона.

 Количество переменных и ограничений в транспортной задаче таково, что для ее решения не обойтись без компьютера и соответствующего программного продукта.