- •1. Матричная алгебра и теория графов в электроэнергетике
- •1.1. Матричная алгебра
- •1.1.1. Классификация матриц
- •1.1.2. Определитель
- •1.1.3. Миноры и алгебраические дополнения
- •1.1.4. Действия с матрицами
- •1.1.5. Транспонированная матрица
- •1.1.6. Обратная матрица
- •1.1.7. Алгоритм вычисления обратной матрицы
- •Основные свойства обратной матрицы
- •Возведение матрицы в степень
- •1.1.8. Нормы матрицы
- •1.1.9. Ранг матрицы
- •1.2. Теория графов в электроэнергетике
- •1.2.1. Некоторые сведения об электрических системах
- •1.2.2. Геометрический образ электрической сети
- •1.2.3. Уравнения законов Ома и Кирхгофа в матричной форме
- •1.2.4. “Прямой ” расчет токораспределения в электрической сети
- •1.2.5. Метод узловых напряжений
- •1.2.6. Метод контурных токов
- •Контрольные вопросы к разделу 1
- •2. Решение систем линейных и нелинейных алгебраических уравнений
- •2.1. Методы решения систем линейных уравнений
- •2.1.1. Метод обратной матрицы
- •2.1.2. Метод определителей
- •2.1.3. Метод Гаусса
- •2.1.4. Вычисление определителя методом Гаусса
- •2.1.5. Вычисление обратной матрицы методом Гаусса
- •2.1.6. Трангуляция матрицы
- •2.1.7. Метод Жордана-Гаусса
- •2.1.8. Метод простой итерации
- •2.1.9. Метод Зейделя
- •2.2. Методы решения систем нелинейных уравнений
- •2.2.1. Понятие о системах нелинейных уравнений и методах их решения
- •Решение нелинейного уравнения методом Ньютона
- •Решение системы нелинейных уравнений методом Ньютона
- •Контрольные вопросы к разделу 2
- •3. Расчет установившихся режимов электрических сетей
- •3.1. Инженерные методы расчета установившихся режимов электрических сетей
- •3.1.1. Расчет установившегося режима разомкнутой электрической сети методом «в два этапа»
- •3.1.2. Расчет установившегося режима кольцевой электрической сети методом в два этапа
- •3.2. Матричные методы расчета установившихся режимов электрических сетей
- •Линейные уун в формуле баланса токов в узлах.
- •3.2.1. Линейные уун в формуле баланса токов в узлах
- •3.2.2. Определение параметров установившегося режима электрической сети по известным значениям
- •3.2.3. Учет поперечной проводимости при использовании уун
- •3.2.4. Нелинейные уун в форме балансов токов в узлах
- •3.2.5. Нелинейные уун в форме балансов мощностей в узлах
- •Контрольные вопросы к разделу 3
- •4. Математическое программирование в электроэнергетике
- •4.1. Математическая модель задачи оптимизации
- •4.2. Характеристика задач оптимизации
- •4.3. Оптимальное распределение потоков мощности в электрической сети
- •4.4. Градиентный метод
- •4.5. Метод наискорейшего спуска
- •4.6. Учет ограничений в форме неравенств
- •Контрольные вопросы к разделу 4
- •Метод наискорейшего спуска.
- •Список литературы
2.1.2. Метод определителей
Известно,
что![]() .
.
Отсюда
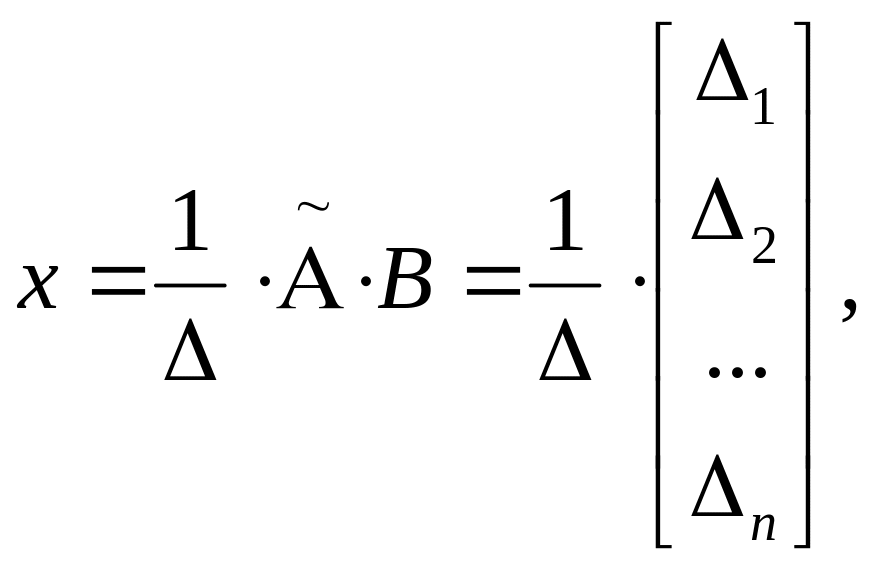 где:
где:
![]() ,
,
![]() ,
… ,
,
… ,
![]()
|
|
|
Итак, метод определителей заключается в вычислении (n+1)-го определителя (∆, ∆1, ∆2, …, ∆n) для матриц n-го порядка. Если число n велико, то вычисление определителей является трудоемкой задачей.
Более распространенным способом решения системы линейных уравнений является метод последовательного исключения неизвестных или метод Гаусса.
2.1.3. Метод Гаусса
Рассмотрим на простейшем примере известный способ исключения неизвестных при решении систем линейных уравнений.
Дана система: |
|
В общем виде: |
|
Умножим
первое уравнение на такой коэффициент
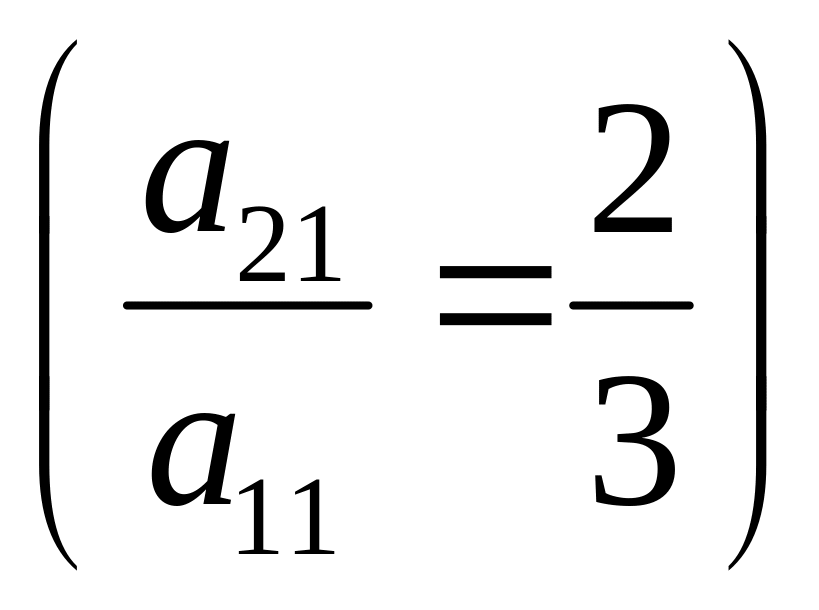 ,
чтобы в обоих уравнениях коэффициент
при х1
стал бы одинаковым
,
чтобы в обоих уравнениях коэффициент
при х1
стал бы одинаковым
|
В
общем виде
|
Теперь вычтем его из второго уравнения, т.е.
-
|
. В общем виде |
-
|
Мы выполнили операцию исключения неизвестной х1из второго уравнения с помощью первого. Запишем систему уравнения после этого исключения следующим образом: первое уравнение записываем в исходном виде, второе – в преобразованном
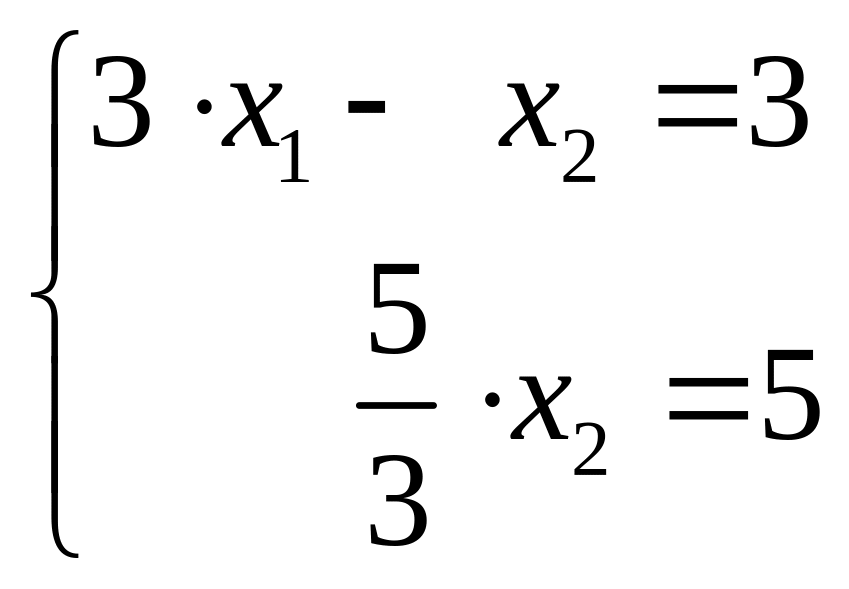 .
.
Второе уравнение содержит лишь одно неизвестное, которое легко вычисляется х2=3. Подставив полученное значение х2 в первое уравнение, можем вычислить и первое неизвестное х1.
Проведенные действия и составляют сущность метода Гаусса. Рассмотрим преобразования по методу Гаусса для системы уравнений n-го порядка.
|
Вычтем
из второго уравнения первое, умноженное
на
![]() .
При этом во втором уравнении будет
обнулен коэффициент при х1.
Затем из третьего уравнения также
вычтем первое, умноженное на
.
При этом во втором уравнении будет
обнулен коэффициент при х1.
Затем из третьего уравнения также
вычтем первое, умноженное на
![]() .
Проделав аналогичные преобразования
с остальными уравнениями системы,
превратим в нуль коэффициенты при x1
во всех уравнениях, кроме первого.
Получим следующую систему:
.
Проделав аналогичные преобразования
с остальными уравнениями системы,
превратим в нуль коэффициенты при x1
во всех уравнениях, кроме первого.
Получим следующую систему:
|
Затем при помощи второго уравнения системы исключим x2 из третьего, четвертого и т.д. уравнений, обнулив коэффициенты второго столбца ниже
 .
.
Последовательно продолжая этот процесс, исключим из системы все коэффициенты, лежащие ниже главной диагонали. В результате получим треугольную систему уравнений
 .
.
Процесс
получения треугольной системы называется
“прямым ходом” по методу Гаусса и
состоит из (n-1)
шагов преобразований. Треугольная
система легко решается “обратным
ходом”. Из последнего уравнения
определяется последнее неизвестное
![]() .
Затем из предпоследнего уравнения
постановкой найденного значения хn
определяется хn-1.
.
Затем из предпоследнего уравнения
постановкой найденного значения хn
определяется хn-1.
После решения системы уравнений методом Гаусса необходимо делать проверку, подставляя в исходные уравнения найденные значения переменных хi(i= 1, …, n).
При решении системы линейных уравнений методом Гаусса все вычисления «прямого хода» можно поместить в следующую таблицу. Рассмотрим таблицу на примере решения системы уравнений третьего порядка.
Уравнения
1), 2) и 3) в таблице составляют искомую
треугольную матрицу после “прямого
хода”. Коэффициенты а11,
,
![]() - называются “ведущими” элементами.
- называются “ведущими” элементами.
№ шага преобразований |
х х1 |
х х2 |
х х3 |
|
|
|
|
|
|
а12 |
а13 |
b1 |
|
0 |
1) |
а21 |
а22 |
а23 |
b2 |
|
|
|
а31 |
а32 |
а33 |
b3 |
|
|
2) |
1 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
2 |
3) |
|
|
|
|
|
При
“обратном ходе” можно использовать
строки таблицы, содержащие единицы,
т.е. вспомогательные уравнения. Имеем
![]() ,далее
,далее
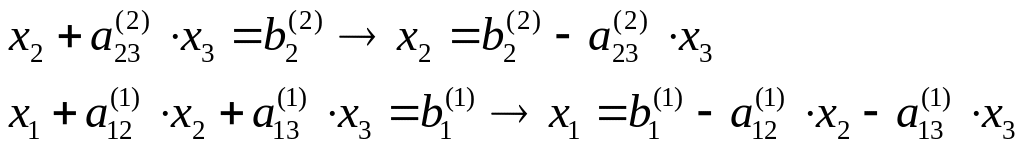 .
.
Пример:
№ шага |
х1 |
х2 |
х3 |
B |
|
|
|
4 |
1 |
2 |
12 |
: 4 |
|
0 |
2 |
8 |
4 |
30 |
|
|
|
1 |
2 |
4 |
17 |
|
|
|
1 |
0,25 |
0,5 |
3 |
х 2 |
х 1 |
1 |
0 |
7,5 |
3 |
24 |
|
|
|
0 |
1,75 |
3,5 |
14 |
|
|
|
|
1 |
0,4 |
3,2 |
х 1,75 |
|
2 |
|
0 |
2,8 |
8,4 |
|
|
Треугольная
система:
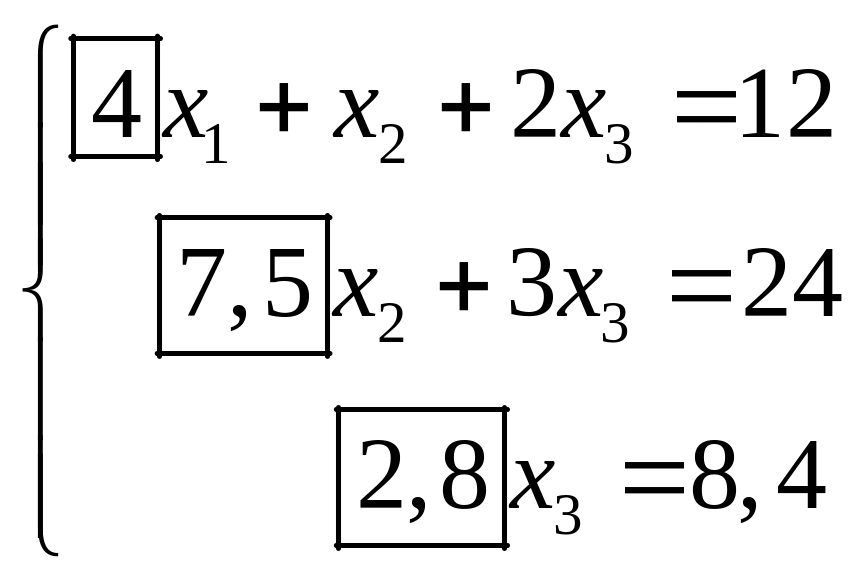 или
или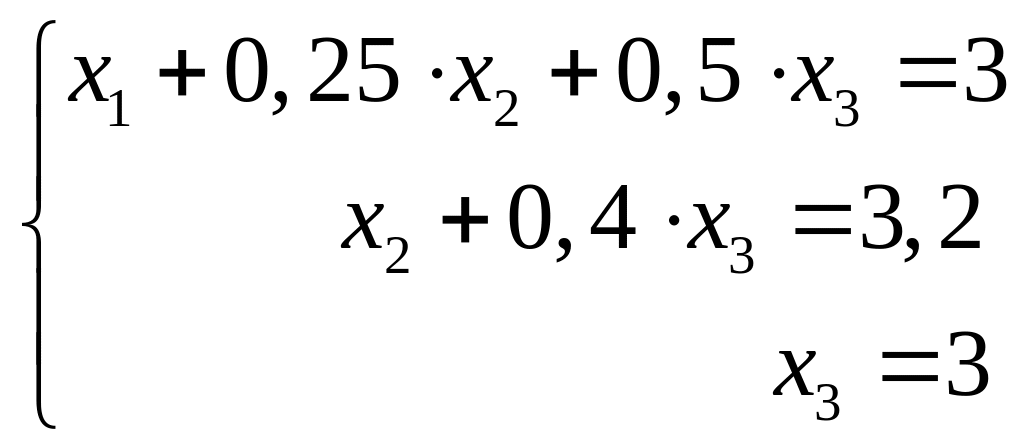
Обратный ход:
|
|

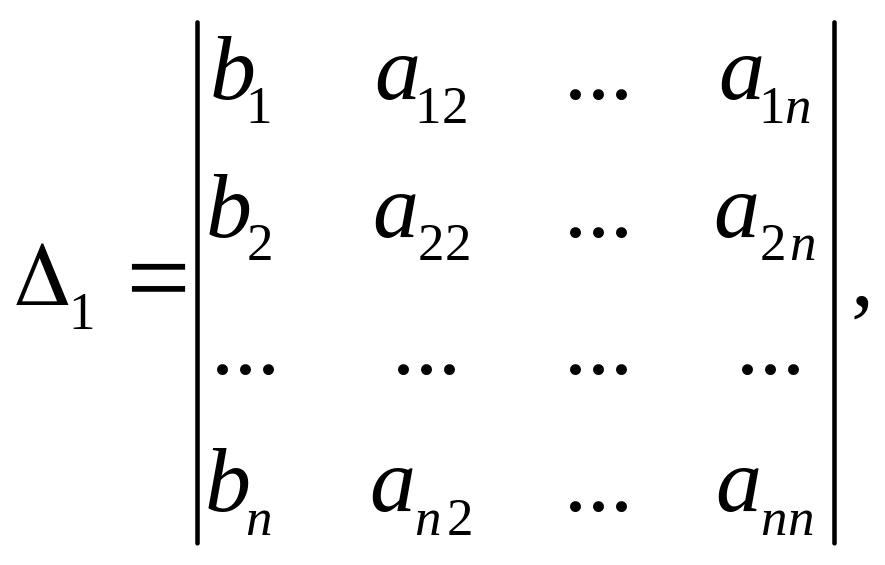
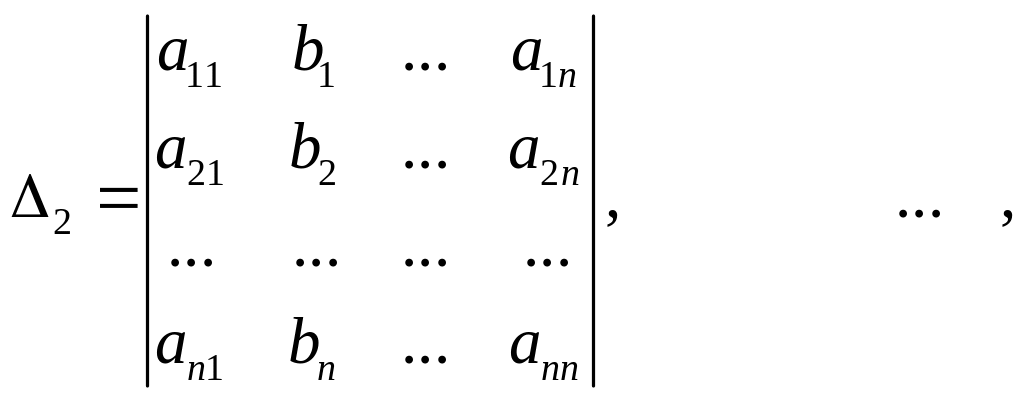
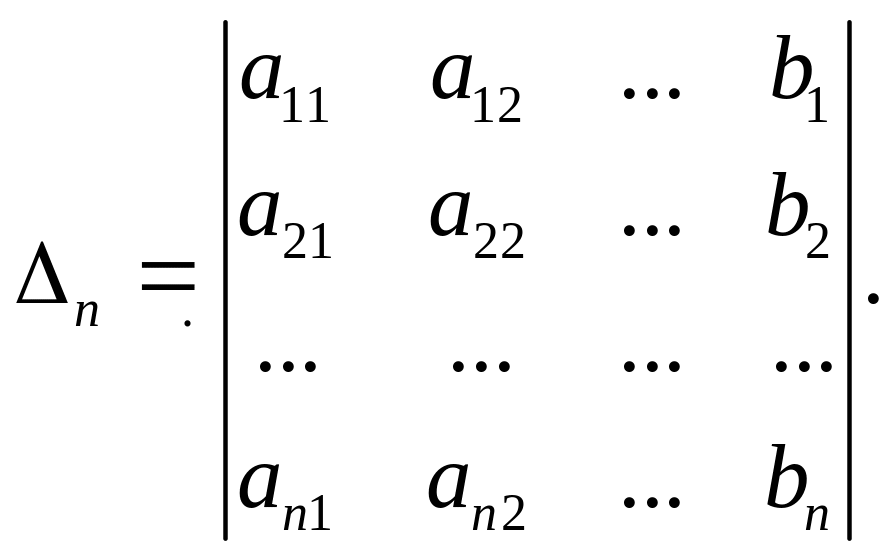
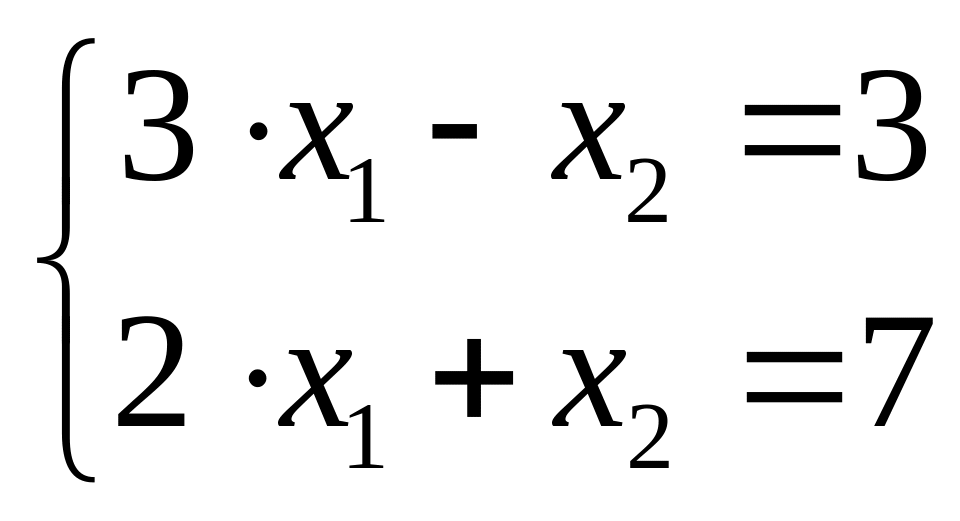
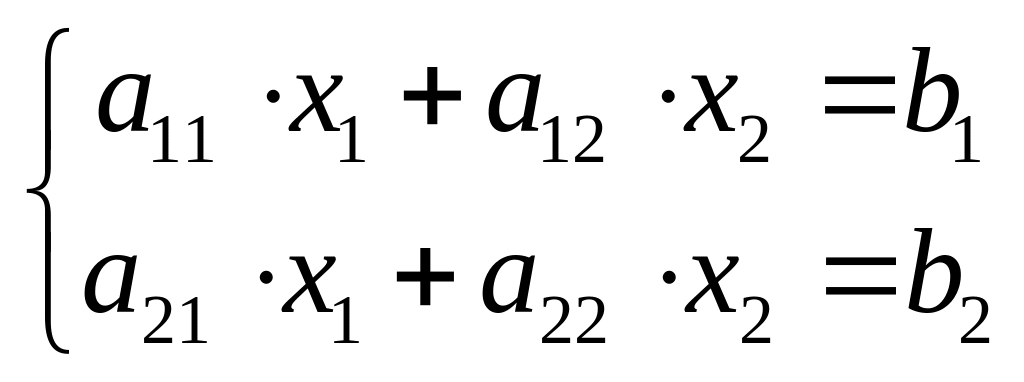
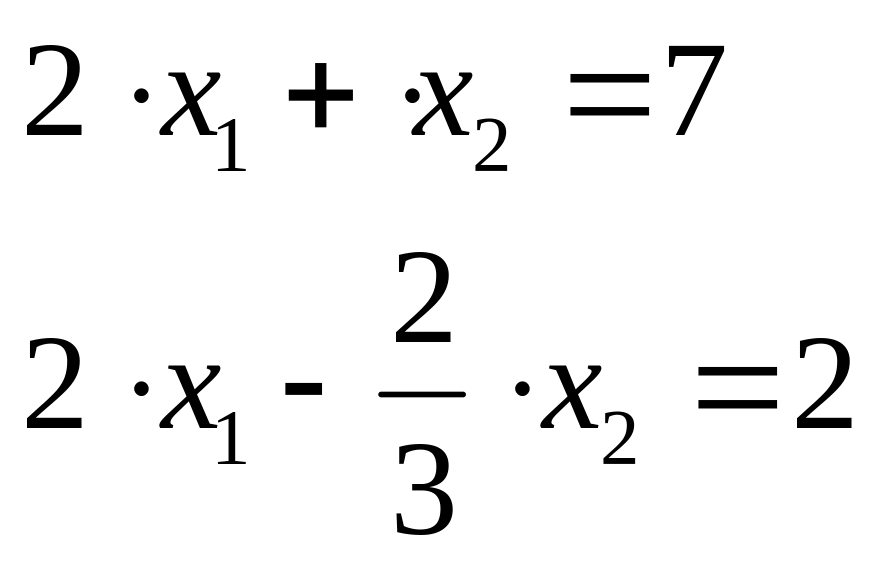
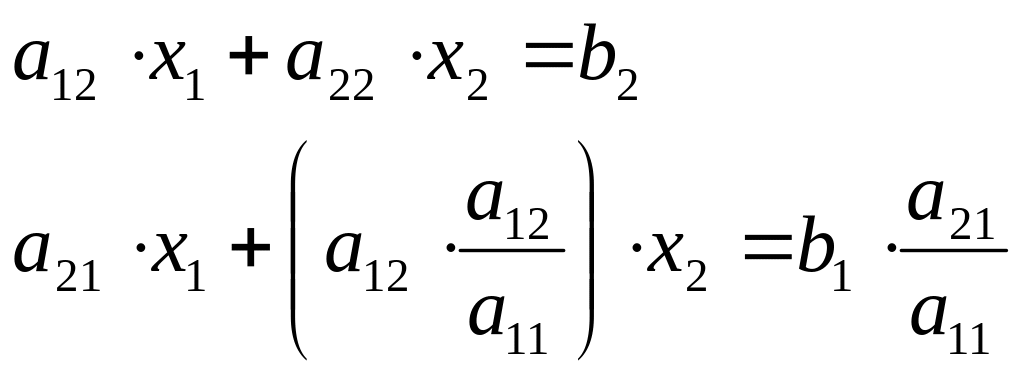
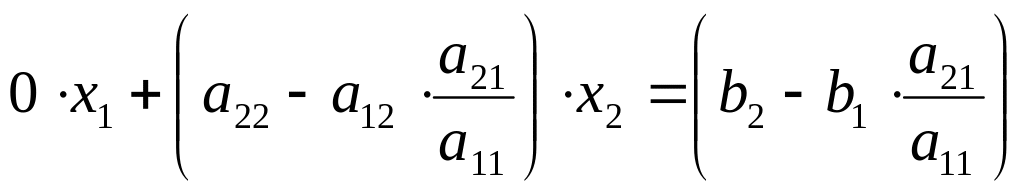
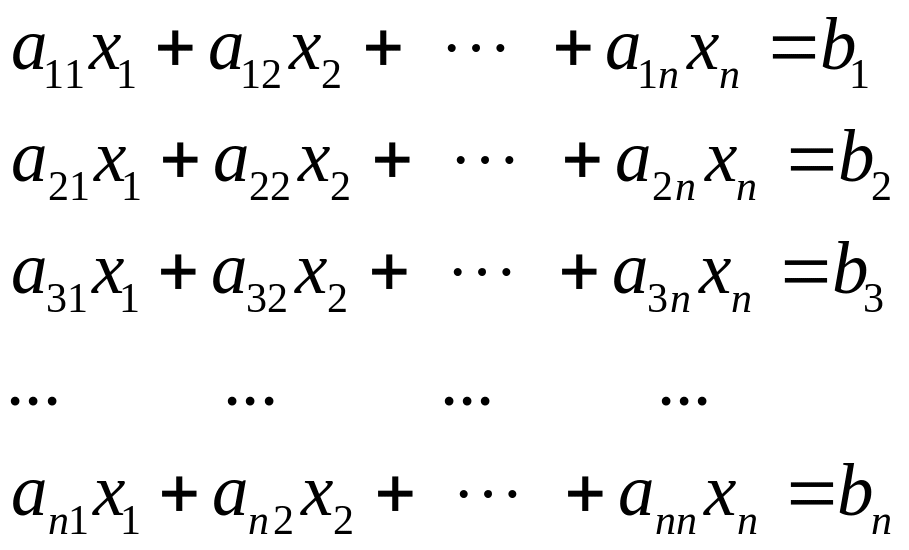 .
.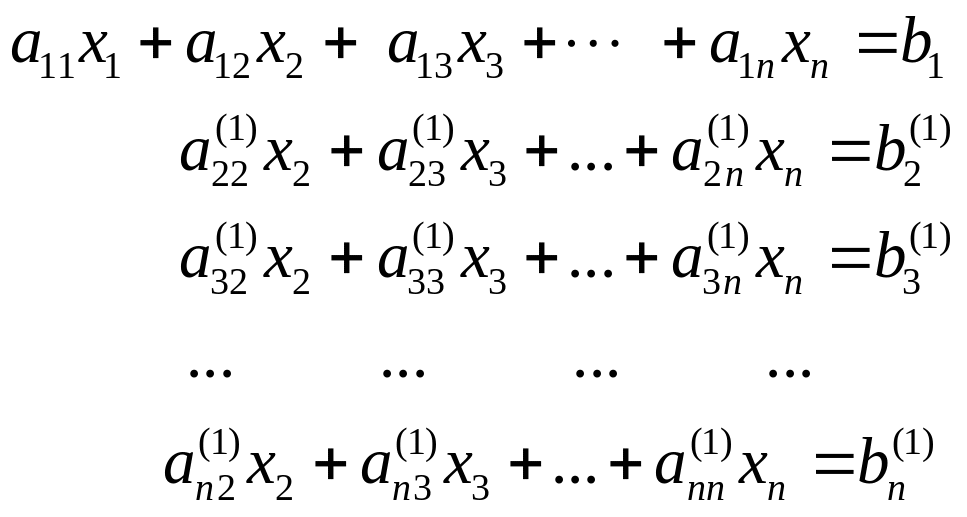 .
. а11
а11 :
а11
:
а11 :
: