Контрольные вопросы к разделу 1

1. Дайте определение матрицы.

2. Какую матрицу называют прямоугольной, квадратной, вектор-строкой, вектор-столбцом, симметричной, неособенной, диагональной, единичной, нулевой, транспонированной?

3. Какие алгебраические операции имеют место в матричной алгебре и как они выполняются?

4. Что такое определитель матрицы, миноры и алгебраические дополнения?

5. Расскажите способ вычисления определителя матрицы разложением по элементам строки или столбца.

6. Дайте определение обратной матрицы.

7. Расскажите алгоритм вычисления обратной матрицы классическим способом.

8. Дайте понятие о графе электрической сети. Независимые узлы и контуры.

9. Расскажите правила формирования первой и второй матриц инциденции графа сети.

10. Напишите законы Ома и Кирхгофа в матричной форме.

11. Напишите уравнение состояния электрической сети в матричной форме для методов узловых напряжений и контурных токов.

12. Расскажите правила формирования матриц узловых проводимостей и контурных сопротивлений.

13. Матричный расчет токов в ветвях линейной электрической цепи методом узловых напряжений и контурных токов.

2. Решение систем линейных и нелинейных алгебраических уравнений

2.1. Методы решения систем линейных уравнений

Методы решения систем линейных уравнений (СЛУ) разделяются на прямые (или точные) и итерационные (или приближенные). Прямые методы представляют собой конечные алгоритмы для вычисления корней системы. Это - метод обратной матрицы, метод определителей, метод Гаусса, метод Жордана-Гаусса, метод “главных элементов”, метод квадратных корней и др. Несмотря на то, что прямые методы называются также точными, результаты вычислений корней СЛУ имеют погрешности вследствие неизбежных округлений при выполнении действий.

Итерационные методы позволяют получать корни СЛУ с заданной точностью путем сходящихся бесконечных вычислительных процессов. К их числу относятся: метод простой итерации, метод Зейделя, метод релаксации и др. Эффективность применения итерационных методов существенно зависят от удачного выбора начальных приближений к корням и быстроты сходимости процесса.

Все вышеперечисленные методы (прямые и итерационные) имеют свои преимущества и недостатки и поэтому для выбора оптимального (лучшего) метода для решения конкретной СЛУ требуются знания пользователя.

Пусть дана система n линейных уравнений с n неизвестными

.

Запишем эту систему в матричном виде

,

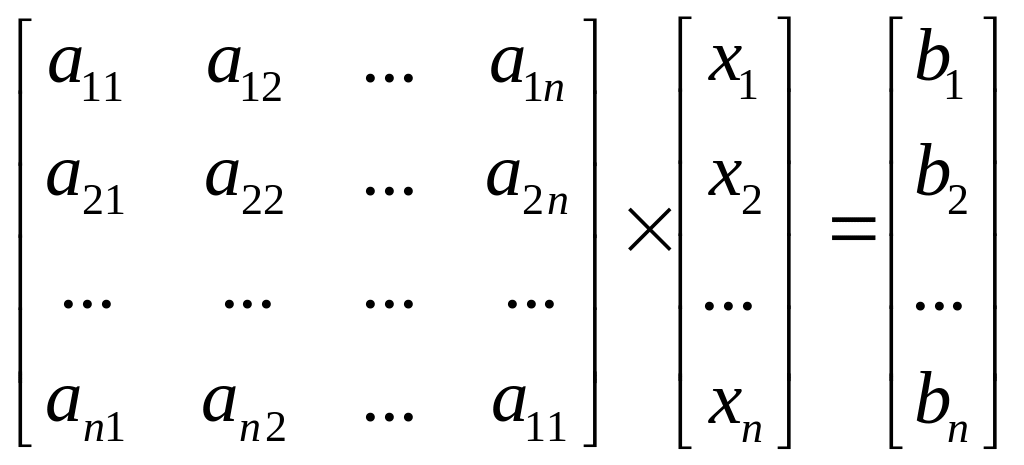или в общем матричном виде

А∙Х=В,

где: А - матрица коэффициентов;

Х – вектор искомых корней СЛУ;

В – вектор свободных членов.

Рассмотрим решение линейной системы уравнений различными методами.

2.1.1. Метод обратной матрицы

Дана система линейных уравнений

А∙Х=В.

Умножим правую и левую части системы на обратную матрицу А^-1

А^-1∙А∙Х= А^-1∙В.

Так как А^-1∙А=Е, то Е∙Х= А^-1∙В.

Так как Е∙Х=Х то, Х= А^-1∙В.

Таким образом, данный метод заключается в нахождении обратной матрицы коэффициентов А^-1 и ее умножении на вектор свободных членов В. Следует иметь ввиду, что с ростом числа уравнений в системе количество выполняемых элементарных операций (сложений, вычитаний, умножений, делений) при использовании метода обратной матрицы нарастает более стремительно чем при использовании других методов, например, метода Гаусса. Метод обратной матрицы для решения СЛУ большой размерности требует больших затрат времени и поэтому редко употребляется.