1.2.2. Геометрический образ электрической сети

Схема замещения электрической сети (или электрической системы в целом) может быть представлена как граф. Вершинами графа при этом являются узлы электрической сети, а ветвями - элементы электрической сети (линии и трансформаторы). Граф сети характеризует ее конфигурацию. Если каждой ветви задать направление, то такой граф называется направленным. Для аналитического представления графа сети необходимо пронумеровать узлы, ветви и независимые контуры, выбрать положительное направление обхода каждого контура (рис.4).

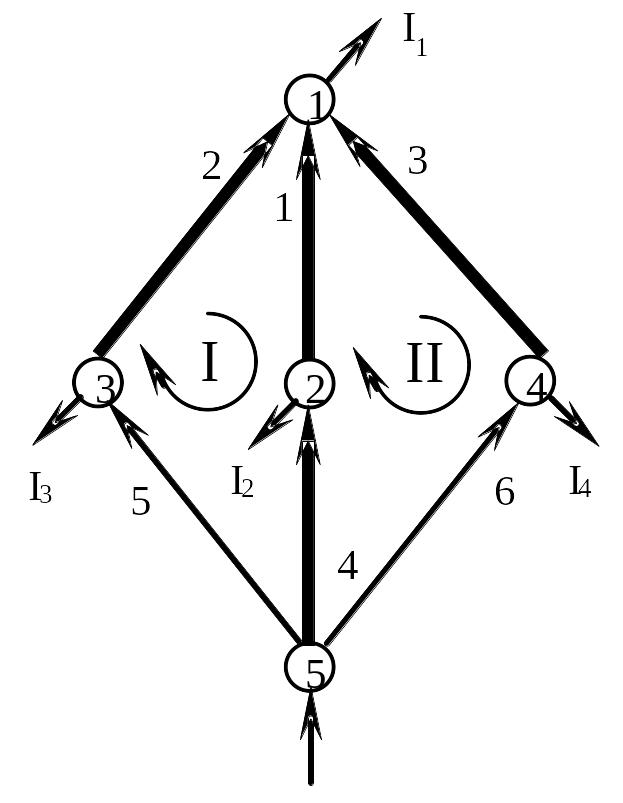
Рис.4. Граф электрической сети

Граф называется полным, если все вершины (узлы) графа соединены (связаны) ветвями друг с другом. Число ветвей в полном графе определяется по формуле , где n – число узлов. В таблице 1 приведено число ветвей в полных графах с различным числом узлов.

Таблица 1.

Число узлов n	2	3	4	5	6	10	100	1000
Число ветвей m	1	3	6	10	15	45	4950	49950

Минимально связанный граф, содержащий в себе всю совокупность вершин графа, называется деревом. Число ветвей в дереве m=n-1. В сложном графе (m>n-1) можно наметить несколько деревьев. На заданном графе жирными линиями выделено одно из возможных деревьев. Ветви, не вошедшие в дерево и дополняющие его до заданного графа, называются хордами. Хорды образуют с ветвями дерева контуры. Дерево контуров не содержит. При расчетах используют такие понятия:

1. число независимых узлов (n-1);

2. число независимых контуров, определяемое по формуле

к=m-(n-1)=m-n+1.

Направленный граф схемы однозначно описывается двумя матрицами инциденций (или соединений). Зная эти матрицы можно нарисовать граф.

Первая матрица инциденций М (узлов и ветвей) представляет собой таблицу, каждая строка которой соответствует одному из узлов, а каждый столбец одной из ветвей. В клетках таблицы проставляется “0”, если ветвь не связана с узлом, которому соответствует строка. Если ветвь связана с узлом, то ставится “+I” или “-I” в зависимости от выбранного направления ветви. Если данный узел является началом ветви, то ставится “+I”, если же ветвь входит в данный узел, который считается концом этой ветви, то ставится “-I”.

				ветви
			1	2	3	4	5	6
	у	1	-1	-1	-1	0	0	0
М =	з	2	+1	0	0	-1	0	0
	л	3	0	+1	0	0	-1	0
	ы	4	0	0	+1	0	0	-1	4 х 6
		5	0	0	0	+1	+1	+1

Информация, которая содержится в последней строке, является избыточной. Поэтому последняя строка, соответствующая узлу n который называется балансирующим, должна быть отброшена. Отброшенную избыточную строку легко можно восстановить, если известны (n-1) строк.

Вторая матрица инциденций N определяет связь между ветвями и контурами. Для сложной электрической сети можно выбрать разные сочетания независимых контуров, поскольку общее число контуров в графе больше. Информация, записываемая для большего числа контуров по сравнению с числом независимых контуров, является избыточной.

				ветви
	к
	о		1	2	3	4	5	6
N =	т	I	-1	0	0	-1	1	0
	у	II	1	0	-1	1	0	1	2 х 6	2 х 6
	р
	ы

Необходимо знать, что выбираемое сочетание независимых контуров должно обязательно содержать все ветви графа. Поэтому независимый контур, который отличается от остальных независимых контуров в выбранном сочетании хотя бы одной ветвью то есть ветвью, которой нет в остальных независимых контурах. В матрице N строки соответствуют независимым контурам, а столбцы ветвям. Если ветвь не входит в рассматриваемый контур, то на пересечении соответствующих строки и столбца ставится “0”. Если ветвь входит в рассматриваемый контур, то ставится “+1” или “-1”.“+1” соответствует совпадению направления ветви и направления обхода контура. “-1” ставится в случае противоположных направлений у ветви и контура.