Возведение матрицы в степень
Возводить степень можно только квадратную матрицу
Свойства:
;
;
.
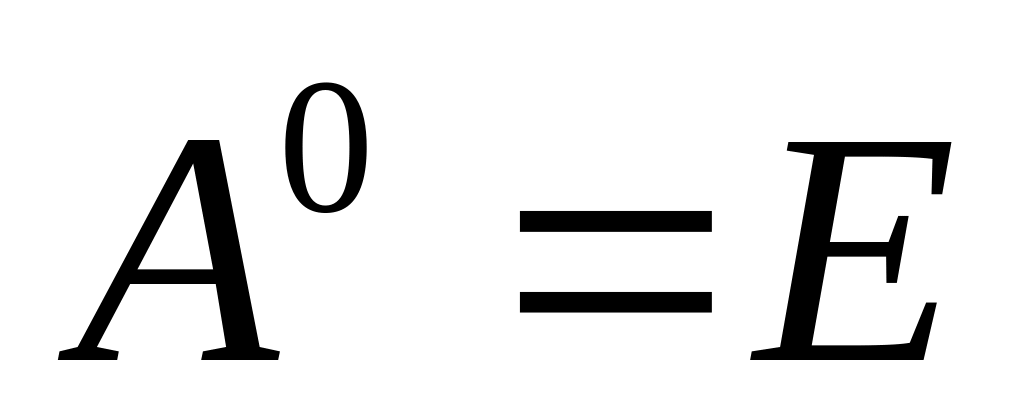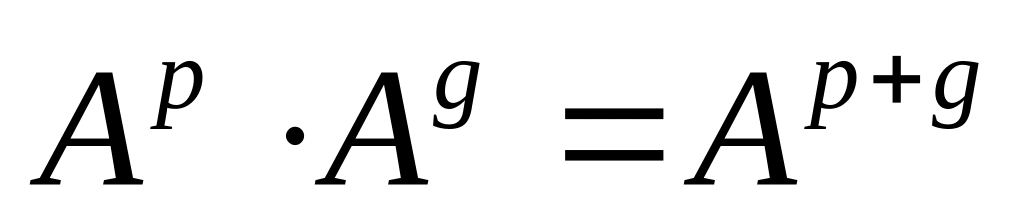1.1.8. Нормы матрицы
Под
нормой матрицы
понимается
действительное число
,
удовлетворяющие условиям:
,
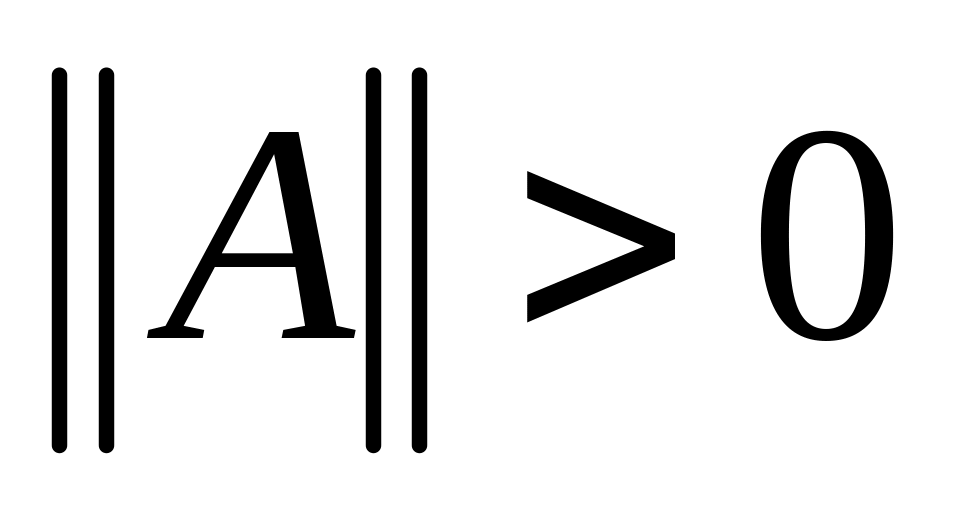причем
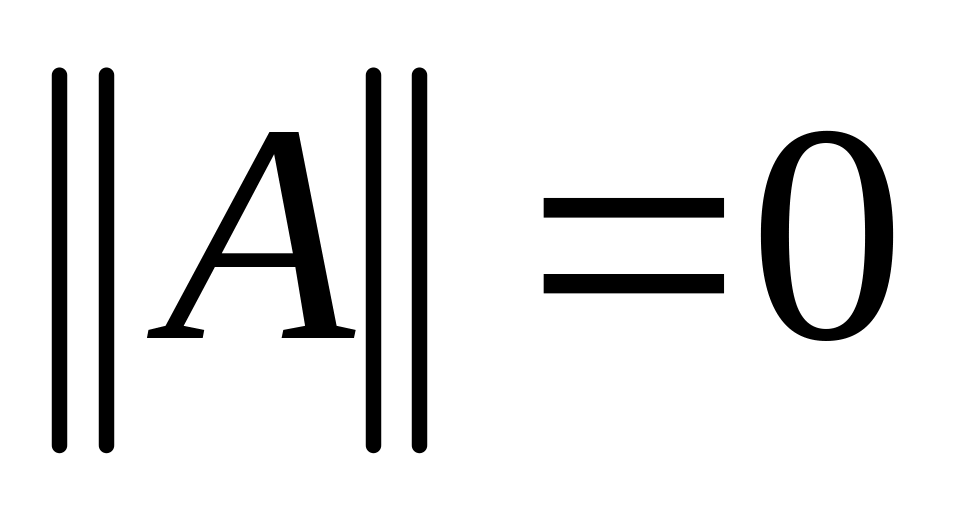только
тогда, когда А=0;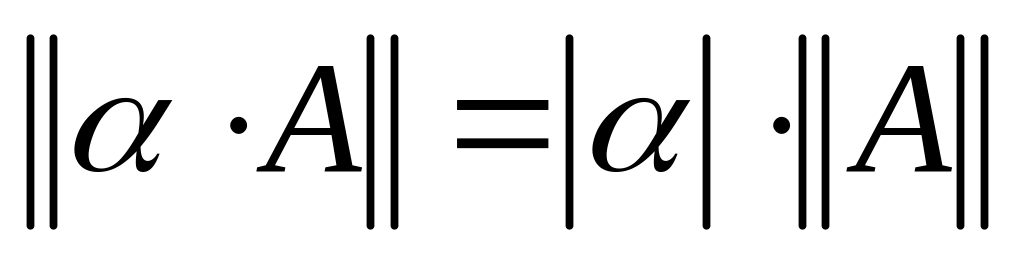
;
;
;
Норма называется канонической, если выполняются еще условия:
При неравенстве
,
.
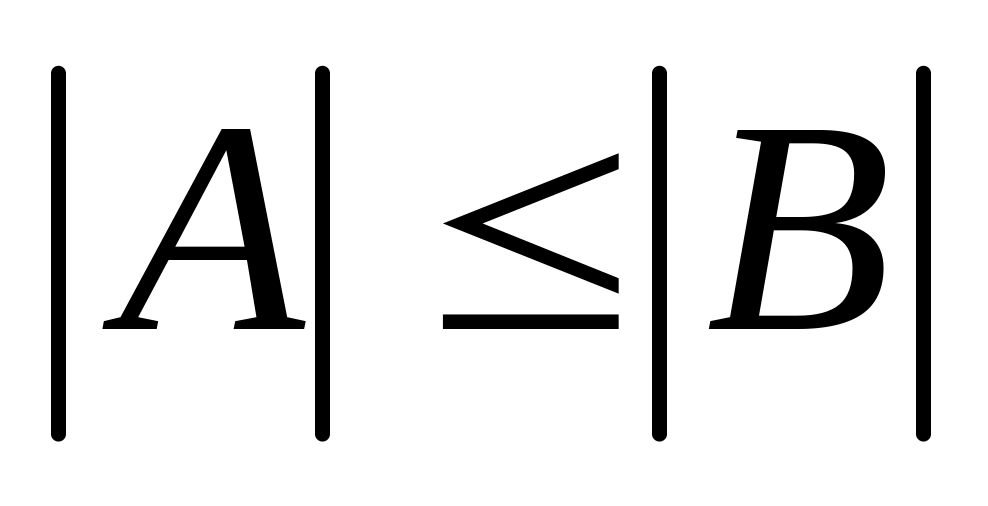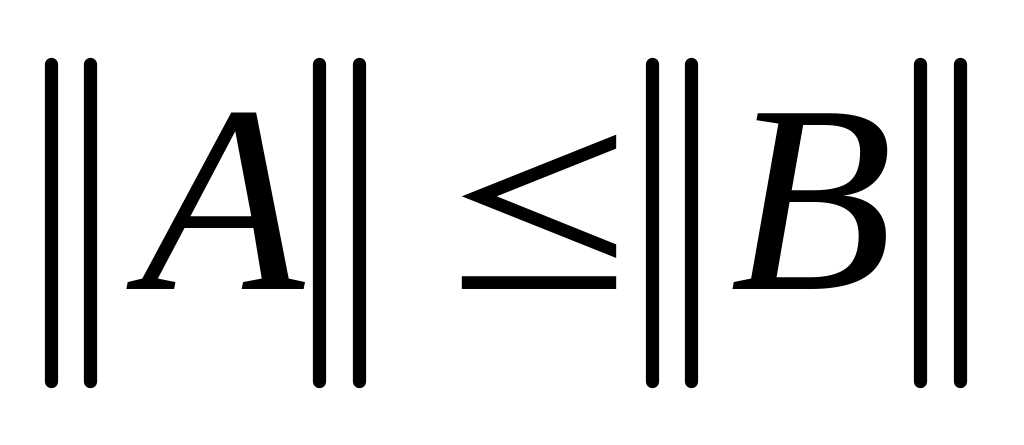Чаще используются три легко вычисляемые нормы:
,
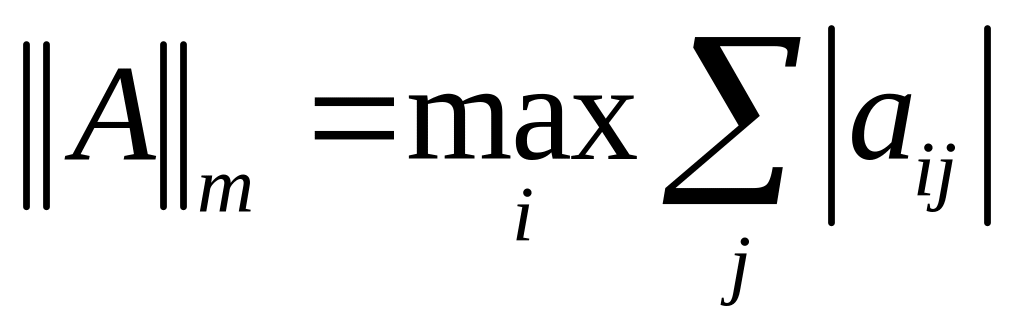(m
– норм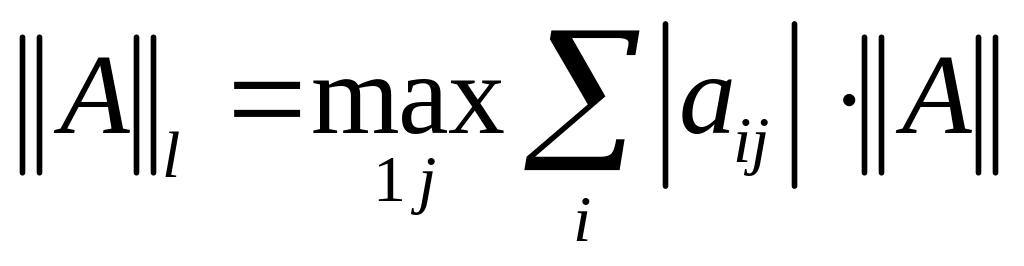а);
,
(l
– норма);
,
(k
– норма).
С помощью норм матриц определяется сходимость итерационных процессов, оценивается погрешность приближений и необходимое число итераций для обеспечения заданной точности нахождения корней СЛУ.
1.1.9. Ранг матрицы
Пусть дана прямоугольная матрица
Если
в этой матрице выбрать производным
образом К строк и К столбцов, то
определитель квадратной матрицы порядка
К, полученной в пересечении выбранных
сток и столбцов, называется минором
К-го порядка матрицы А(k≤min
(m,n)).
Ранг матрицы к называется максимальный
порядок минора матрицы, отличного от
нуля. Ранг нулевой матрицы равен нулю.
Разность
-
называется дефектом матрицы.
При нахождении ранга матрицы следует придерживаться следующих правил:
переходить от миноров меньших порядков (начиная с миноров первого порядка, т.е. элементов матриц) к минорам больших порядков;
если найдем минор (r+1)-го порядка, окаймляющий минор Д. Если эти миноры равны нулю, то ранг матрицы равен r. Если же хотя бы один из них не равен нулю, то эту операцию следует применять к нему и т.д.
1.2. Теория графов в электроэнергетике
1.2.1. Некоторые сведения об электрических системах
Следует иметь в виду, что предлагаемая дисциплина читается до изучения основных курсов по специальности 140204 (100100). Поэтому для того, чтобы приблизить излагаемый материал не только по содержанию, но и по форме к будущим специальным курсам, вспомним некоторые понятия, уже знакомые по курсу “Введение в специальность”.
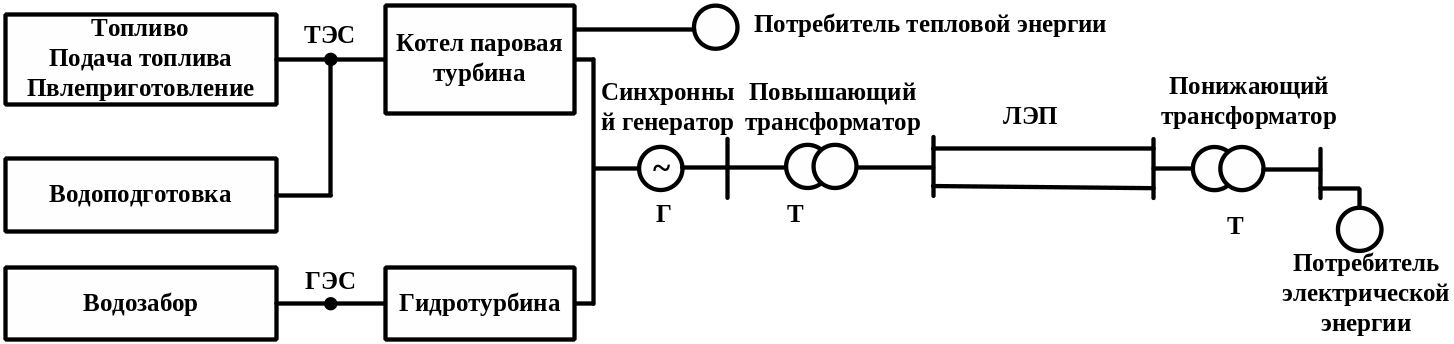Рис.1.
Принципиальная схема энергосистемы
Энергетическая система начинается с топлива и воды и заканчивается потребителям тепловой и электрической энергии (рис.1).
Электрическая система начинается с генератора и кончается потребителем электрической энергии, т.е. электрическая система – это электрическая часть энергетической системы, состоящая из совокупности элементов, вырабатывающих, преобразующих, передающих, распределяющих и потребляющих электроэнергию.
Электрическая сеть начинается с повышающего трансформатора и кончается потребителем электрической энергии.
Работа электрической системы прежде всего характеризуется значениями мощностей в МВт (и энергии в МВт∙час), вырабатываемых, преобразуемых, передаваемых и потребляемых всеми ее элементами.
Режим электрической системы – это ее состояние в любой момент времени, которое характеризуется совокупностью электрических параметров или параметров режима.
Параметры режима – это напряжение в различных точках системы, токи в ее элементах, углы расхождения векторов ЭДС и напряжений, активные и реактивные мощности генераторов, потоки активной и реактивной мощности в линиях и трансформаторах, потери мощности и напряжения в элементах системы и т.д.
При анализе различают два основных вида режимов электросистем:
установившийся режим, который может быть нормальным или послеаварийным (когда какой-либо элемент выведен из работы в ремонт);
переходный режим, который может быть нормальным или аварийным (короткое замыкание, обрыв фаз и др.).
Установившиеся режимы в электрической системе описываются законами Ома и Кирхгофа или вытекающими из них уравнениями узловых напряжений (УУН) и уравнениями контурных токов (УКТ). Математический анализ установившихся режимов работы электрических систем сводится к составлению и решению систем линейных и нелинейных алгебраических уравнений. Наиболее широко применяемые при анализе установившихся режимов электрических систем методы решения линейных и нелинейных алгебраических уравнений будут изложены во втором разделе данного курса лекций.
Переходные процессы описываются системами дифференциальных уравнений, методы решения которых в данной дисциплине не рассматриваются. Переходные процессы электрических систем основательно изучаются в специальных дисциплинах на старших курсах.
Электрической схемой системы называется графическое изображение последовательности соединения ее элементов между собой. Элементы электрической системы обладают активными и реактивными (индуктивными или емкостными) сопротивлениями и проводимостями. Если заменить в электрической схеме элементы системы их сопротивлениями и проводимостями, то получим схему замещения электрической системы. Расчеты и анализ режимов электрической системы производятся на основе ее схемы замещения. Каждый элемент системы имеет свою схему замещения. Воздушные линии электропередачи напряжением 110 - 220 кВ обычно представляются П-образной схемой замещения, а двухобмоточный трансформаторы – Г-образной. Для примера на рис.1 и 2 приведены соответственно электрическая схема условной сети, состоящая из двух подстанций ПС1 и ПС2 с двумя трансформаторами каждая и двухцепной ВЛ, и ее схема замещения.
Рис.2. Электрическая схема сети
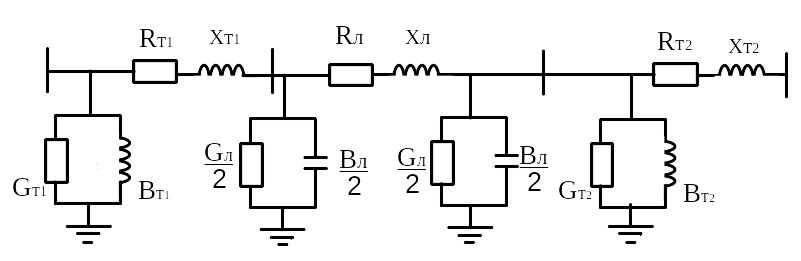
Рис.3. Схема замещения
Перед тем, как начать рассчитывать режим работы электрической системы (т.е. определять параметры режима) составляют схему замещения электрической системы (или сети) и вычисляют все параметры схемы замещения – сопротивления и проводимости. Электрическая схема сети и ее схема замещения, представленные на рис.1 и 2, очень малы, и рассчитать режимы для такой схемы можно “вручную”. Однако реальные электрические системы и сети достигают больших размеров и без использования современной вычислительной техники и специально разработанных компьютерных программ выполнить расчет режимов электрических систем и сетей невозможно. Использование же для указанной цели специальных программно-вычислительных комплексов (ПВК) на персональных компьютерах (ПК) основано на применении матричной алгебры и теории графов.