4.6. Учет ограничений в форме неравенств

При поиске оптимального режима ЭЭС, как правило, задается система ограничений в виде неравенств. Эти ограничения определяют область допустимых решений. Ограничения налагаются на параметры режима из условий качества и надежности электроснабжения потребителей. Так, в заданных пределах должны находиться напряжения в узлах, мощности источников, коэффициенты трансформации и т.д.

Рассмотрим учет ограничений в форме неравенств в методе приведенного градиента. Все переменные представляются в виде двух векторов – вектора зависимых переменных х и вектора независимых переменных у, то есть z = х, у.

Вначале рассмотрим учет ограничений на вектор у. При этом возможны три случая:

Y₂

1 .

Исходная т.0 находится в ОДР. Мы можем двигаться по антиградиенту из т.0 в т.I. Но при этом нужно следить, чтобы выбирая ньютоновский шаг t_н, близкий к t_* мы не вышли за пределы ОДР (т.е. надо следить, чтобы ). Но для этого надо знать . Как его определить?

Если шагаем из т.0 в т. , то будем иметь

, где , а задано предварительно.

∆Y₂ – допустимое изменение переменной Y₂

Отсюда

Такие вычисления должны быть выполнены по всем переменным Y_i, i=1, …, n-m. Поскольку мы выбираем одинаковый шаг при движении в направлении каждой переменной, то из всех дополнительных шагов t_i_доп нужно выбирать минимальный. Тогда ни одна переменная не выйдет за пределы ОДР.

2 .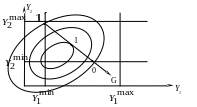

Исходная т.0 находится на границе ОДР. Антиградиент – G направлен внутрь ОДР, направление движения допустимо, величина шага должна контролироваться как в первом случае

3 .

Исходная т.0 находится на границе ОДР. Антиградиент – G направлен за пределы ОДР. Следовательно, движение по антиградиенту является недопустимым. Однако не все компоненты градиента ведут к нарушению ограничений, т.е. компоненты градиента, которые составляющая антиградиента q₁, приводит к нарушению ограничений и поэтому ее приравнивают к нулю. Двигаться будем по направлению проекции антиградиента q₂ вдоль границы. .

Для учета ограничений на зависимые переменные х используется смена базиса, т.е. в случае нарушения ограничения какой-либо зависимой переменной в процессе, эта переменная переводится в состав вектора у, а взамен ее в вектор х из вектора у переводится переменная, значения которой далеки от предельных.

Известен также другой способ учета ограничений в форме неравенств – метод штрафных функций. Он применяется в тех случаях, когда ограничения не являются жесткими. Предполагается как бы неограниченное изменение переменных, но при нарушении какого-либо ограничения значения минимизируемой функции резко возрастает за счет добавления к целевой функции штрафа