Контрольные вопросы к разделу 3
1. Понятие об электрической сети и режимах ее работы.
2. Понятие о схеме замещения электрической сети и ее параметрах.
3. Схема замещения воздушной линии.
4. Схема замещения двухобмоточного трансформатора.
5. Потери мощности и зарядная мощность в воздушной линии.
6. Потери мощности в двухобмоточном трансформаторе.
7. Векторная диаграмма падения напряжения в элементе сети.
8. Расчет режима разомкнутой электрической сети методом "в два этапа".
9. Расчет режима кольцевой электрической сети методом "в два этапа".
10. Понятие о матричных методах расчета: установившихся режимов электрических сетей. Этапы решения задачи.
11. Линейные уравнения установившегося режима электрической сети.
12. Нелинейные уравнения установившегося режима в форме баланса узловых токов.
13. Уравнения установившегося режима в форме баланса узловых мощностей.
14. Понятие о способах и методах решения систем нелинейных уравнений установившихся режимов электрических сетей.
15. Определение параметров установившегося режима электрической сети по известным значениям рабочих напряжений в узлах.
4. Математическое программирование в электроэнергетике
Это раздел вычислительной математики, в котором изучаются методы решения оптимизационных задач (или задач оптимизации).
В электроэнергетике задачи оптимизации можно разделить на:
эксплуатационные или задачи функционирования систем энергетики;
проектные или задачи развития систем энергетики.
К оптимизационным задачам функционирования систем энергетики относятся такие:
минимизация потерь активной мощности в электрической сети;
наивыгоднейшее распределение активной нагрузки между агрегатами тепловой электростанции (ТЭС);
выбор оптимального состава работ агрегатов на ТЭС;
и другие.
К оптимизационным задачам развития систем энергетики относятся такие:
оптимизация структур генерирующих мощностей в энергосистеме (ОЭЭС или ЕЭЭС);
оптимизация электростанций (выбор мощности электростанций, количество единичной мощности агрегатов, сроков их ввода);
оптимизация графика сработки-наполнения водохранилища ГЭС;
и другие.
4.1. Математическая модель задачи оптимизации
Оптимизационная задача формулируется следующим образом:
Найти минимум целевой функции (или функции цели):
|
(1) |
при соблюдении ограничений в виде равенств (или условий связи)
|
(2) |
,
и неравенств
|
(3) |
,
.В качестве целевой функции (1) в электроэнергетике часто используются следующие критерии оптимальности:
приведенные затраты на строительство и эксплуатацию систем энергетики З, млн. руб.
расход топлива на ТЭС В, т.у.т.
издержки на расход топлива на ТЭС И, млн. руб.
В качестве условий связи (2) в задачах электроэнергетики часто используются уравнения установившегося режима. В том числе: уравнения закона Кирхгофа, УУН, УКТ.
В качестве неравенств накладывающиеся на переменные задач оптимизации обычно выступают ограничения пропускной способности ЛЭП, в том числе по нагреву или динамической устойчивости.
Задача оптимизации заключается в нахождении оптимума (чаще минимум) целевой функции и оптимальных значений переменных.
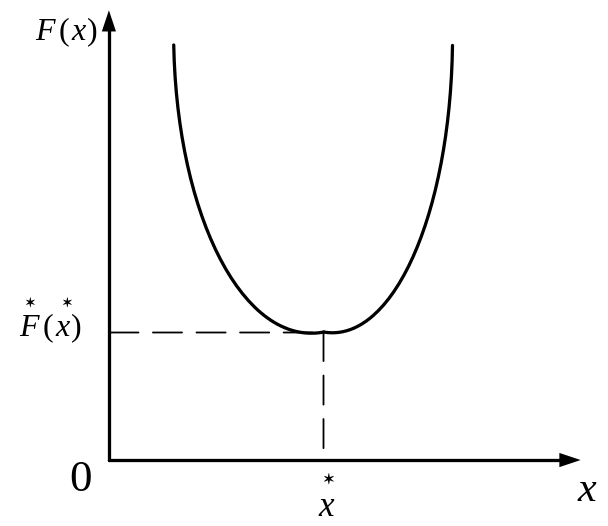
Сложность решения оптимизационных задач практически заключается в том, что функции (1)-(2), могут быть нелинейными с разрывами 1-ого и 2-ого рода, а переменные задачи xi, могут быть как непрерывными, так дискретными величинами. В качестве непрерывных величин могут быть использованы потоки мощности в элементах сети, а в качестве дискретных – сечение проводов, номинальное напряжение.