2. Решение системы нелинейных уравнений методом Ньютона

Система нелинейных уравнений решается методом Ньютона аналогично.

Пусть дана система нелинейных уравнений

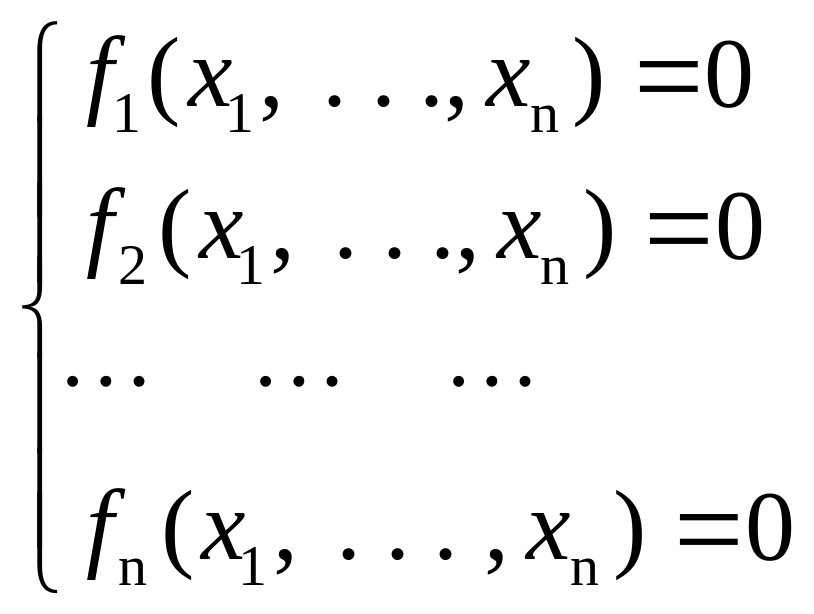
Эта система заменяется системой линеаризованных уравнений

;

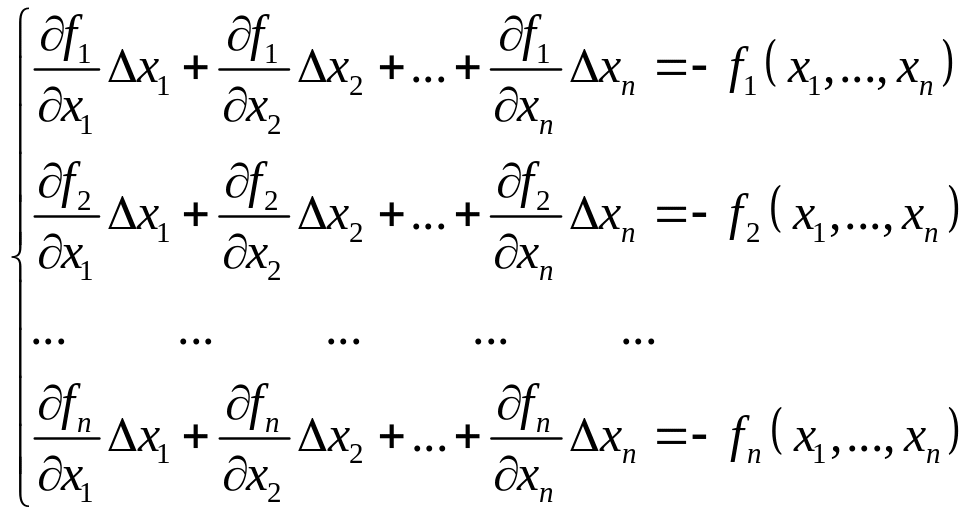В матричном виде система (2) записывается

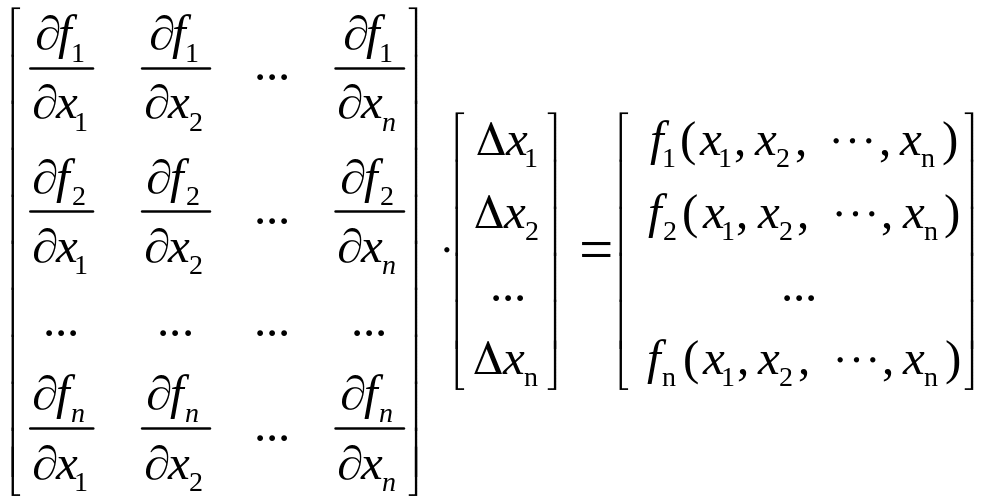
или в общем матричном виде

(8)

где - матрица Якоби; ∆х – вектор-столбец поправок; F(х) – вектор-столбец невязок.

Данная система линейных уравнений может быть решена любым известным численным методом (например, методом Гаусса).

Алгоритм решения системы нелинейных уравнений методом Ньютона состоит из следующих действий:

1. Зададим начальные приближения , , …, .

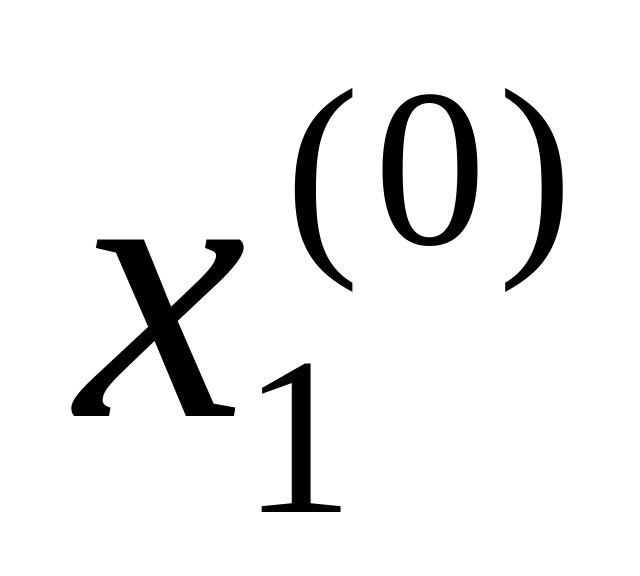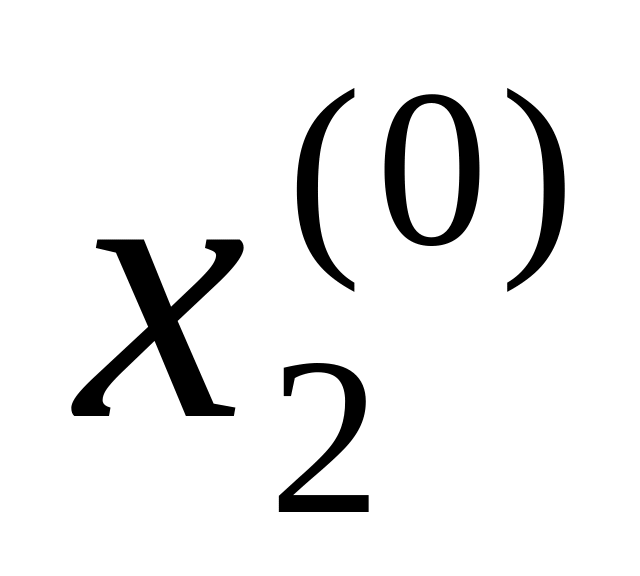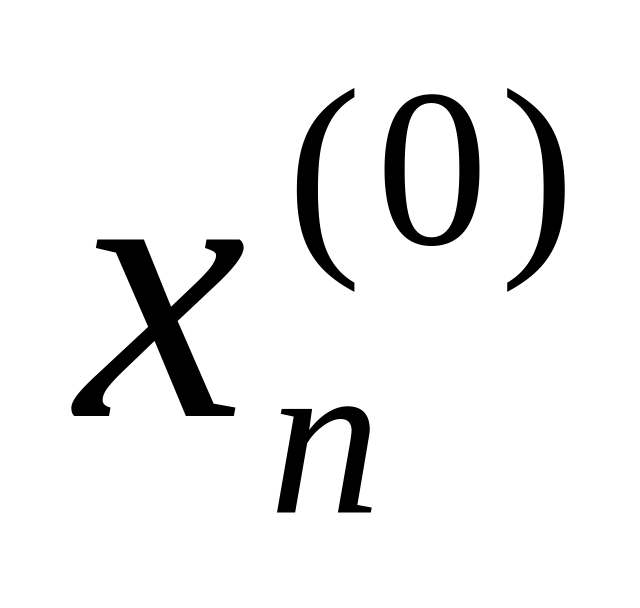2. Вычислим невязки f₁(х₁, х₂, …, х_n), f₂(х₁, х₂, …, х_n), …, f_n(х₁, х₂, …, х_n).

3. Вычислим все элементы матрицы частных производных при х₁= 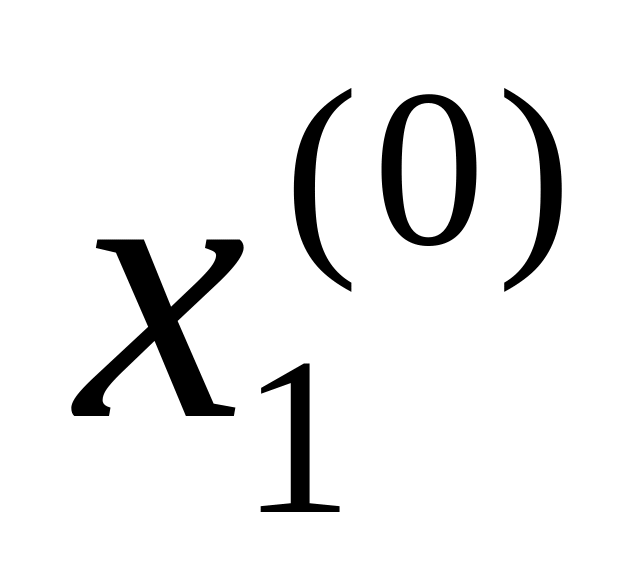, х₂= , …, х_n= .

4. Найдем поправки , , …,

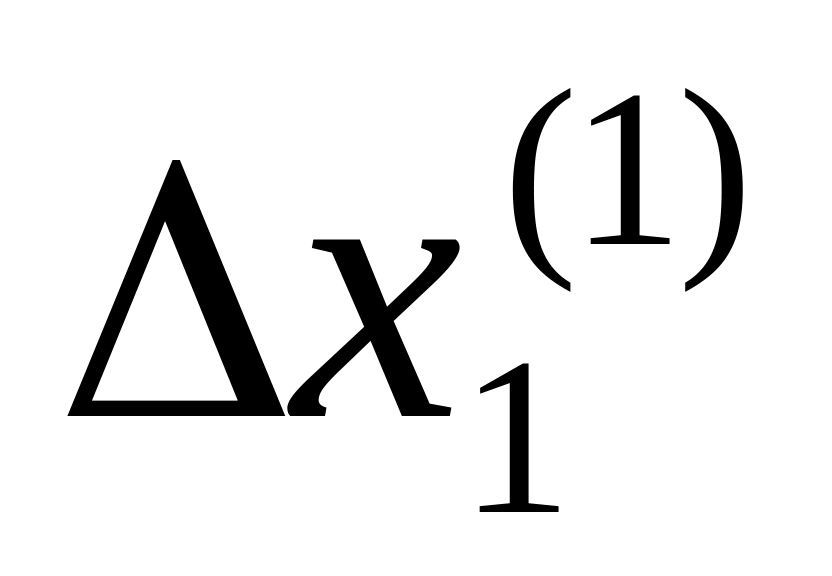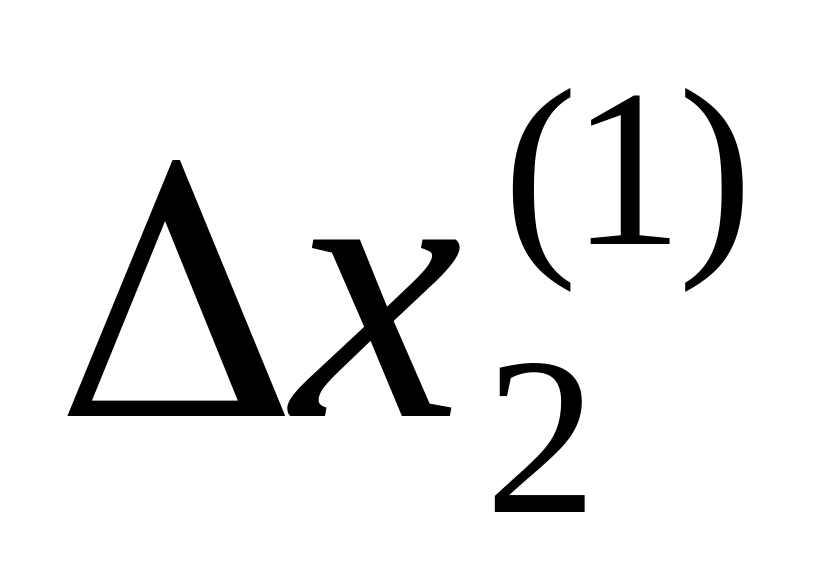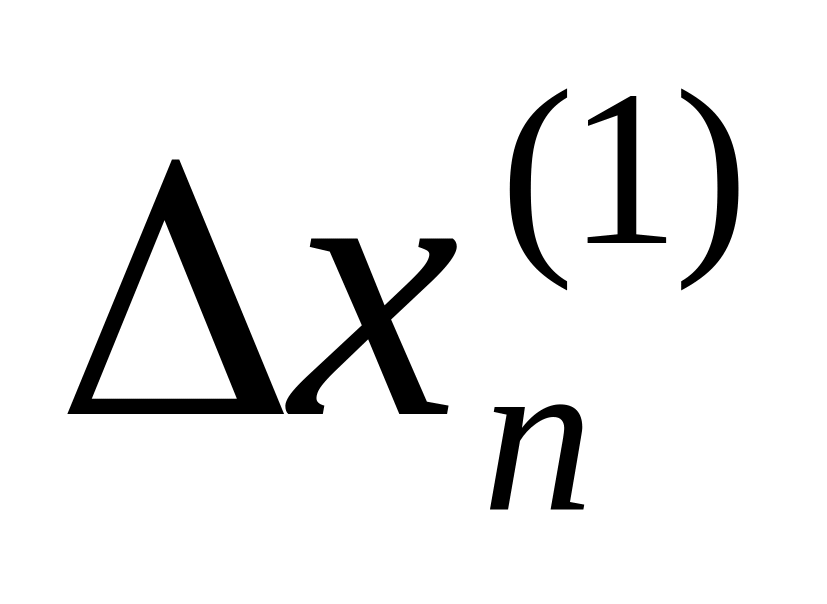
Для этого решим систему линейных уравнений

численным методом относительно поправок ∆х⁽¹⁾.

5. Определим новые приближения

6. Вычислим невязки f₁(х₁,…, х_n), f₂(х₁,…, х_n), …, f_n(х₁,…, х_n)

7. Проверим условия

.

Если не выполняется хотя бы одно из n условий, то производим следующую итерацию – повторяем действия 3-7, уже используя полученные значения , , …, . Итерационный процесс нахождения корней системы нелинейных уравнений будем продолжать до выполнения всех условий без исключения.

Метод Ньютона эффективен в том случае, когда известны хорошие начальные приближения неизвестных, достаточно близкие к корням системы нелинейных уравнений. Это условие в наших задачах, как правило, удается выполнить.

Пример:

Нужно решить систему нелинейных уравнений

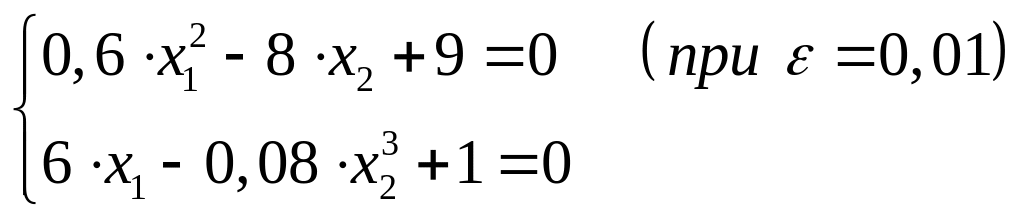
0 итерация ;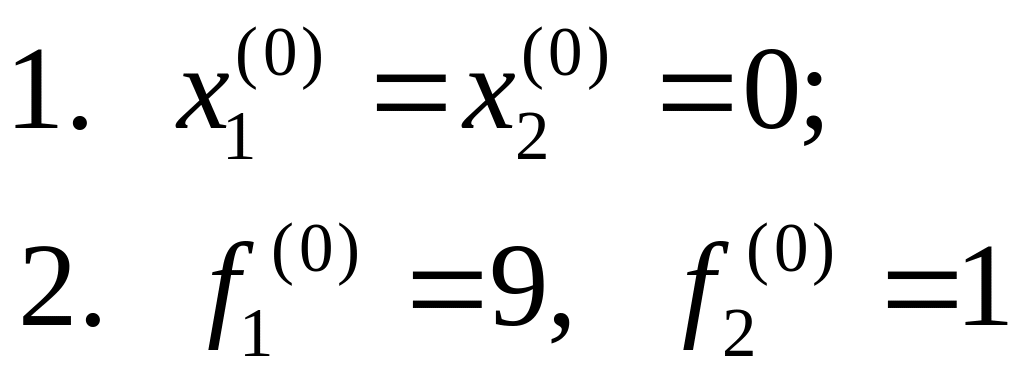

1 итерация

1.

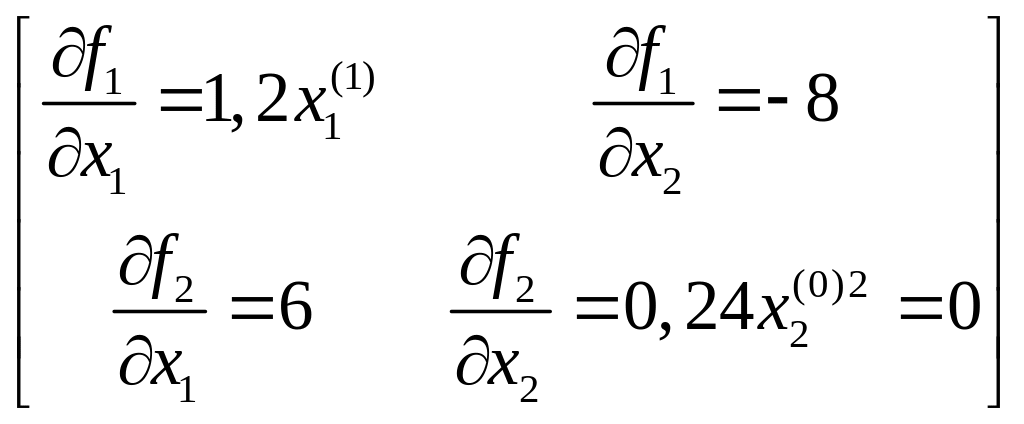
2. 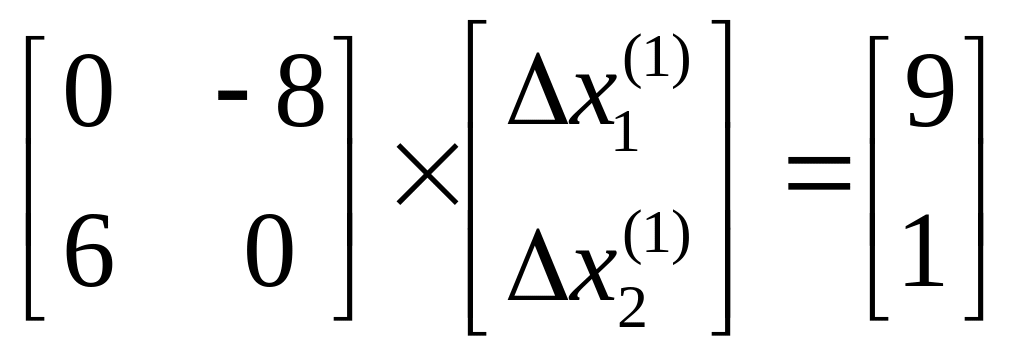или ;

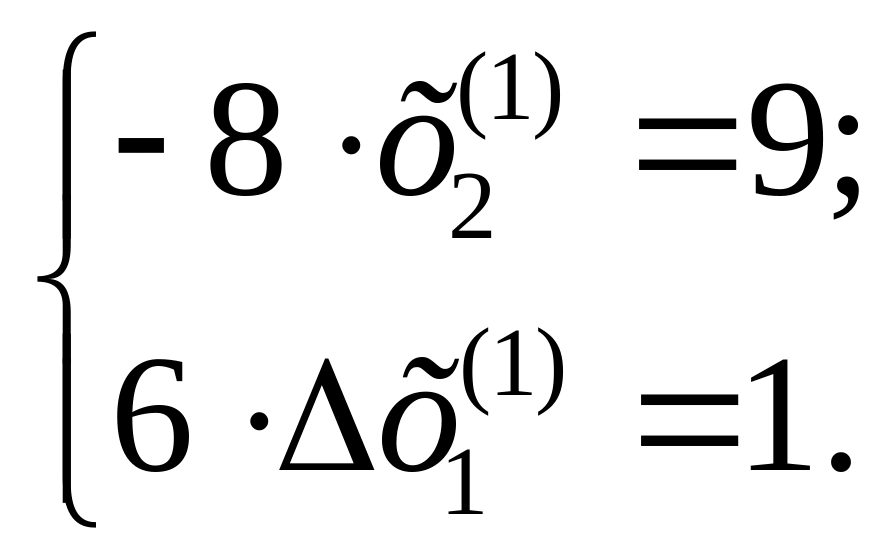Отсюда

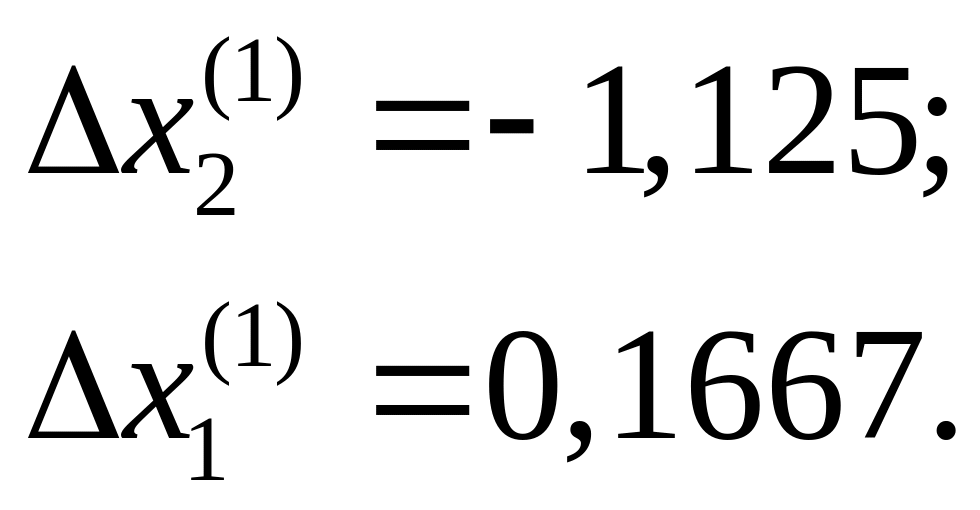
3.

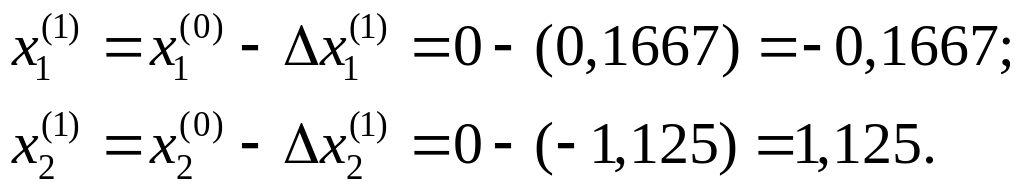
4. ; |0,01667|>ε

; |0,114|>ε

2 итерация

1.

2. ;

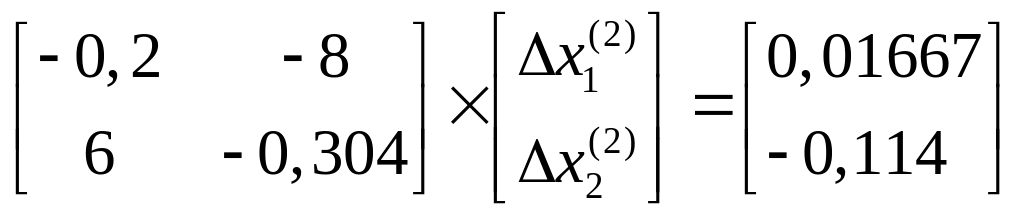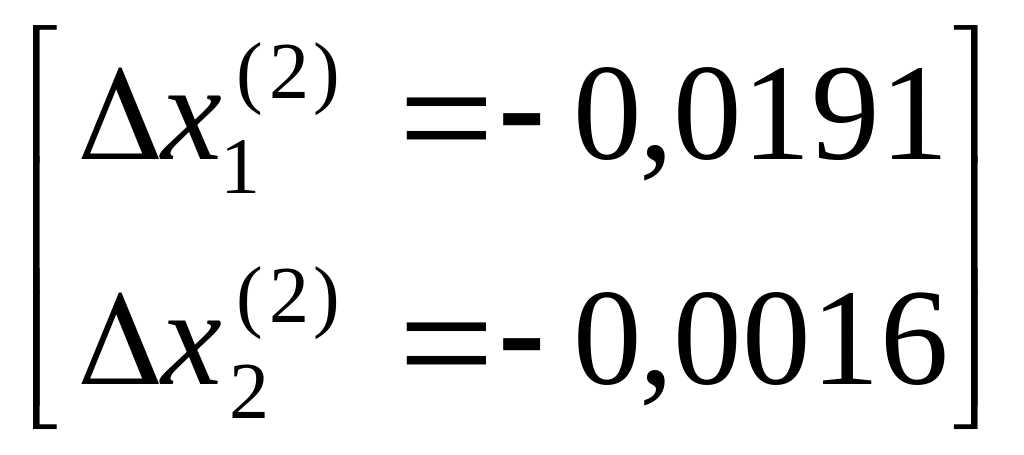
3. ;

;

4. 0,0002714<ε

0,0000071<ε

Результаты расчетов сведем в таблицу

№ итерации		∆х		хк		f(к)
0	-	-		0	0	9	1
1		0,1667	-1,125	-0,1667	1,125	0,01667	0,114
2		-0,0191	-0,0016	-0,1476	1,1266	0,0002714	0,0000071

Контрольные вопросы к разделу 2

1. Сущность точных и итерационных методов решения СЛУ.

2. Метод обратной матрицы.

3. Метод определителей.

4. Метод Гаусса.

5. Вычисление определителя методом Гаусса.

6. Метод Гаусса без обратного хода.

7. Вычисление определителя методом Гаусса.

8. Преимущества и недостатки метода Гаусса.

9. Метод простой итерации.

10. Метод Зейделя.

11. Основное условие сходимости итерационного процесса решения СЛУ.

12. Преимущества и недостатки итерационных методов решения СЛУ.

13. Понятие о нелинейных уравнениях, описывающих режимы электрических систем.

14. Методы простой итерации и Зейделя для решения нелинейных уравнений.

15. Сущность линеаризации нелинейных уравнений.

16. Метод Ньютона как метод касательных для решения нелинейного уравнения.

17. Алгоритм метода Ньютона для решения СНУ.