2. Решение нелинейного уравнения методом Ньютона

Рассмотрим применение метода Ньютона сначала для решения одного нелинейного уравнения f(х)=0, где f(х) - непрерывно дифференцируемая функция.

Функцию f(х) можно разложить в ряд Тейлора в окрестностях произвольно взятой точки х⁽⁰⁾

.

(1)

Если в многочлене (1) отбросить производные высших порядков и оставить только линейные члены, то получим

(2)

где - называется поправкой.

Эта операция называется линеаризацией нелинейного уравнения.

Из линеаризованного уравнения (2) можно выразить поправку

(3)

и вычислить новое (первое) приближение к корню

.

(4)

Если подставить значение в f(х), то получим невязку . По величине невязки можно судить о близости к корню. Если невязка значительно отличается от нуля, то требуется вычислять новую поправку , подставляя в линеаризованное уравнение (2) значение . Вычислительная процедура повторяется до тех пор, пока очередная невязка не станет достаточно близкой к нулю.

Таким образом, суть метода Ньютона заключается в линеаризации нелинейного уравнения и решении полученного линейного уравнения на каждой итерации. Значение корня линейного уравнения является очередным приближением к корню решаемого нелинейного уравнения.

Графическая иллюстрация применения метода Ньютона для решения нелинейного уравнения f(х)=0 дана на рисунке.

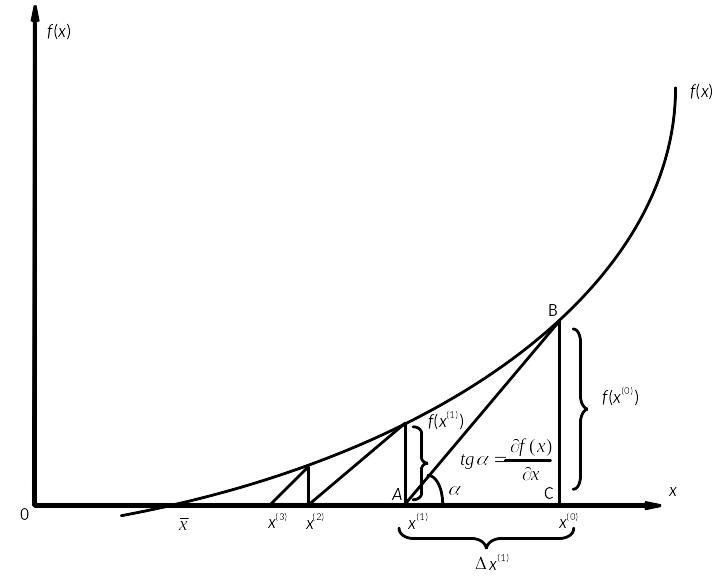
Рис.2.1. Графическая иллюстрация применения метода Ньютона

Как видно из рисунка, к действительному корню нелинейного уравнения приближаемся последовательно от заданного начального приближения х⁽⁰⁾.

Алгоритм решения нелинейного уравнения f(х)=0 методом Ньютона состоит из следующих действий:

1. Задаем начальное приближение х⁽⁰⁾.

2. Вычисляем невязку f(х⁽⁰⁾).

3. Определяем 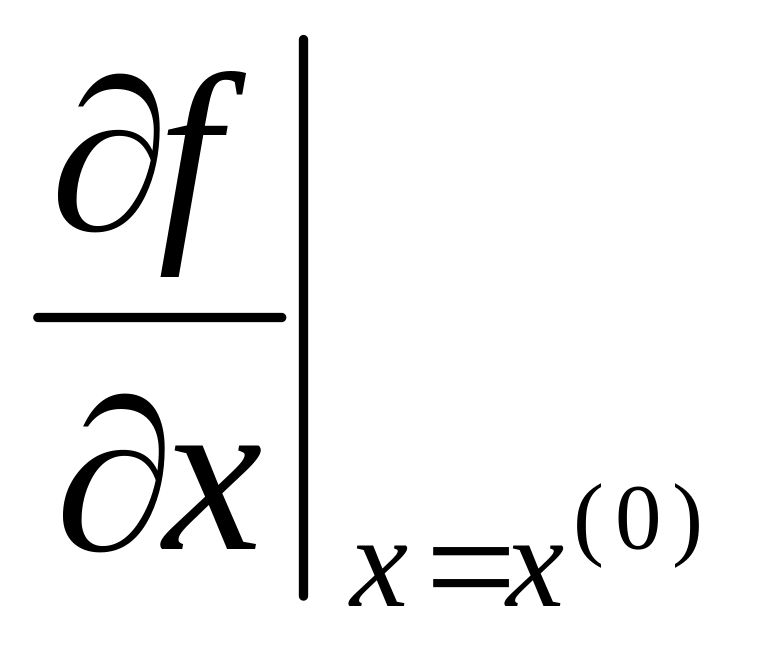- значение производной (как тангенс угла , образованного касательной к кривой в точке В с осью х).

4. Вычисляем поправку ∆х⁽¹⁾ (как катет АС прямоугольного треугольника АВС).

.

5. О

   f(х)

   пределяем новое приближение х⁽¹⁾=х⁽⁰⁾-∆х⁽¹⁾ .

6. Вычисляем невязку f(х⁽¹⁾) и проверяем условие ε.

Если условие выполняется, то вычислительный процесс заканчивается, в противном случае повторяем действия начиная с 3-го.

Примечание: 1. Значение ε задается в каждом конкретном случае и не должно быть равным нулю, так как итерационный метод не позволяет определить абсолютно точное значение корня (это обычно практически не требуется). Неоправданное снижение значения ε не рекомендуется, поскольку при этом увеличивается число итераций.

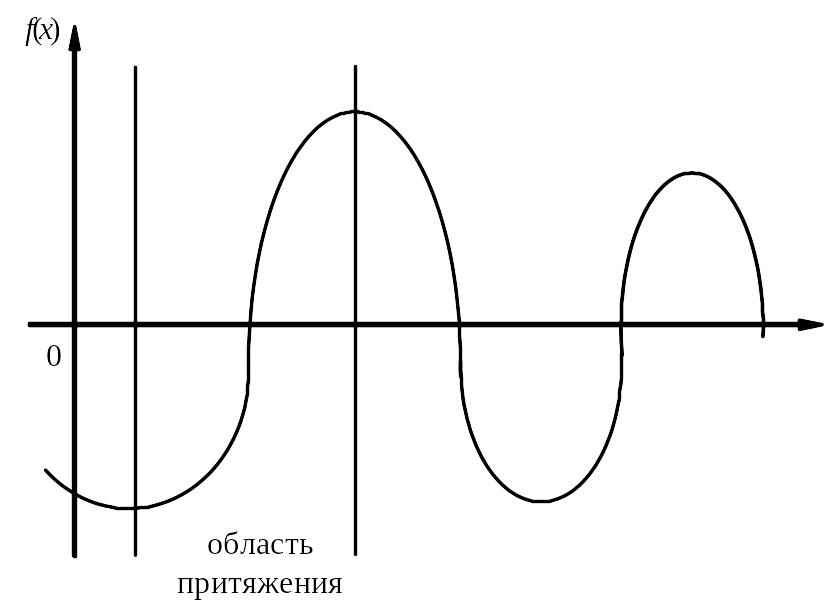
2. Если у функции f(х)=0 имеется несколько корней, то метод Ньютона позволяет найти вещественный корень и причем только один в области притяжения которого находится начальное приближение.

Пример:

Нужно решить нелинейное уравнение 7х³+5х-1=0 (ε = 0,01)

0 итерация		Зададим х(0)=0
		Начальная невязка f(х(0))=1| ≥ε

1 итерация

|0,056| > ε

2 итерация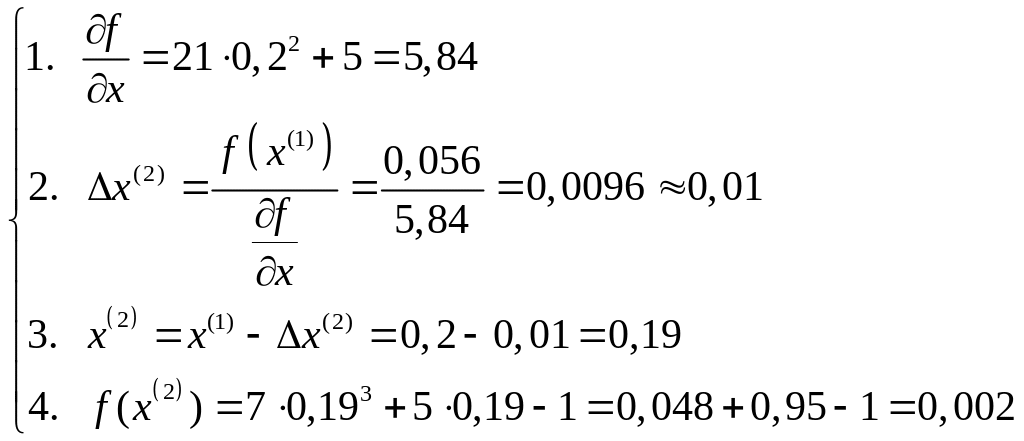

|0,002|< ε

Результаты расчетов целесообразно представить в следующей таблице

№ итерации (к)	тангенс	∆х(к) поправка	х(к) приближение	f(х(к)) невязка
0	-	-	0	-1
1	5	-0,2	0,2	0,056
2	5,84	0,01	0,19	0,002