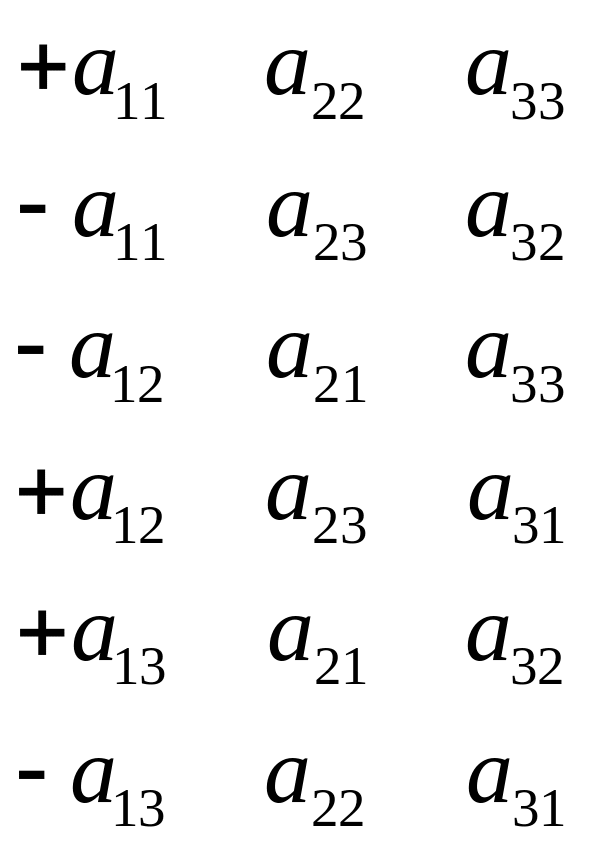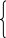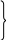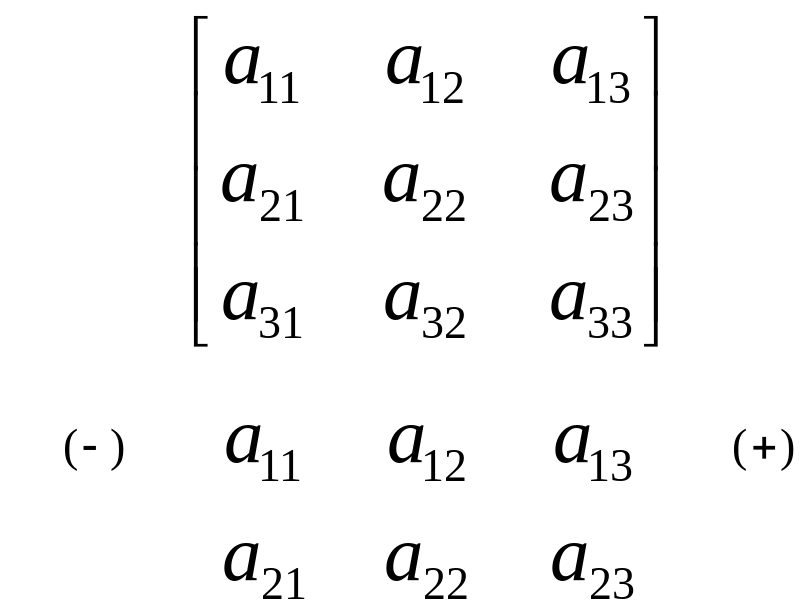Министерство образования и науки Российской Федерации

Иркутский государственный технический университет

Факультет энергетический

Кафедра электрических станций, сетей и систем

МАТЕМАТИЧЕСКИЕ ЗАДАЧИ

ЭЛЕКТРОЭНЕРГЕТИКИ

Конспект лекций

для бакалавров, обучающихся по направлению 140400 «Электроэнергетика и электротехника» и профилям подготовки: «Электрические станции», «Электроснабжение»,«Электропривод и автоматика»

Иркутск 2012 г.

СОДЕРЖАНИЕ

1. МАТРИЧНАЯ АЛГЕБРА И ТЕОРИЯ ГРАФОВ В ЭЛЕКТРОЭНЕРГЕТИКЕ 4

1.1. МАТРИЧНАЯ АЛГЕБРА 4

1.1.1. Классификация матриц 4

1.1.2. Определитель 5

1.1.3. Миноры и алгебраические дополнения 6

1.1.4. Действия с матрицами 8

1.1.5. Транспонированная матрица 9

1.1.6. Обратная матрица 9

1.1.7. Алгоритм вычисления обратной матрицы 10

1.1.8. Нормы матрицы 11

1.1.9. Ранг матрицы 12

1.2. ТЕОРИЯ ГРАФОВ В ЭЛЕКТРОЭНЕРГЕТИКЕ 12

1.2.1. Некоторые сведения об электрических системах 12

1.2.2. Геометрический образ электрической сети 14

1.2.3. Уравнения законов Ома и Кирхгофа в матричной форме 16

1.2.4. “Прямой ” расчет токораспределения в электрической сети 19

1.2.5. Метод узловых напряжений 19

1.2.6. Метод контурных токов 21

Контрольные вопросы к разделу 1 22

2. РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ И НЕЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ 24

2.1. МЕТОДЫ РЕШЕНИЯ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ 24

2.1.1. Метод обратной матрицы 24

2.1.2. Метод определителей 25

2.1.3. Метод Гаусса 25

2.1.4. Вычисление определителя методом Гаусса 28

2.1.5. Вычисление обратной матрицы методом Гаусса 28

2.1.6. Трангуляция матрицы 29

2.1.7. Метод Жордана-Гаусса 31

2.1.8. Метод простой итерации 33

2.1.9. Метод Зейделя 37

2.2. МЕТОДЫ РЕШЕНИЯ СИСТЕМ НЕЛИНЕЙНЫХ УРАВНЕНИЙ 38

2.2.1. Понятие о системах нелинейных уравнений и методах их решения 38

2.2.2. Решение нелинейного уравнения методом Ньютона 39

2.2.3. Решение системы нелинейных уравнений методом Ньютона 42

Контрольные вопросы к разделу 2 45

3. РАСЧЕТ УСТАНОВИВШИХСЯ РЕЖИМОВ ЭЛЕКТРИЧЕСКИХ СЕТЕЙ 46

3.1. ИНЖЕНЕРНЫЕ МЕТОДЫ РАСЧЕТА УСТАНОВИВШИХСЯ РЕЖИМОВ ЭЛЕКТРИЧЕСКИХ СЕТЕЙ 46

3.1.1. Расчет установившегося режима разомкнутой 46

электрической сети методом «в два этапа» 46

3.1.2. Расчет установившегося режима кольцевой 51

электрической сети методом в два этапа 51

3.2. МАТРИЧНЫЕ МЕТОДЫ РАСЧЕТА УСТАНОВИВШИХСЯ РЕЖИМОВ ЭЛЕКТРИЧЕСКИХ СЕТЕЙ 54

3.2.1. Линейные УУН в формуле баланса токов в узлах 55

3.2.2. Определение параметров установившегося режима электрической сети по известным значениям 56

узловых напряжений 56

3.2.3. Учет поперечной проводимости при использовании УУН 56

3.2.4. Нелинейные УУН в форме балансов токов в узлах 60

3.2.5. Нелинейные УУН в форме балансов мощностей в узлах 61

Контрольные вопросы к разделу 3 62

4. МАТЕМАТИЧЕСКОЕ ПРОГРАММИРОВАНИЕ 64

В ЭЛЕКТРОЭНЕРГЕТИКЕ 64

4.1. Математическая модель задачи оптимизации 64

4.2. Характеристика задач оптимизации 65

4.3. Оптимальное распределение потоков мощности 66

в электрической сети 66

4.4. Градиентный метод 70

4.5. Метод наискорейшего спуска 72

4.6. Учет ограничений в форме неравенств 81

Контрольные вопросы к разделу 4 83

Список литературы 84

1. Матричная алгебра и теория графов в электроэнергетике

1.1. Матричная алгебра

1.1.1. Классификация матриц

Система чисел, действительных или комплексных, расположенных в прямоугольной таблице из строк и столбцов называется матрицей

,

где:	–элементы матрицы; –номера строк; –число строк в матрице; –номера столбцов; –число столбцов.

Для матрицы часто используется сокращенная запись ,где

m,·n–размерность матрицы.

Если , то матрица называется квадратной.

Если , то матрица называется прямоугольной.

Если , то матрица – скаляр.

Если , а , то матрица называется вектор-строкой .

Если ,а , то матрица называется вектор-столбцом .

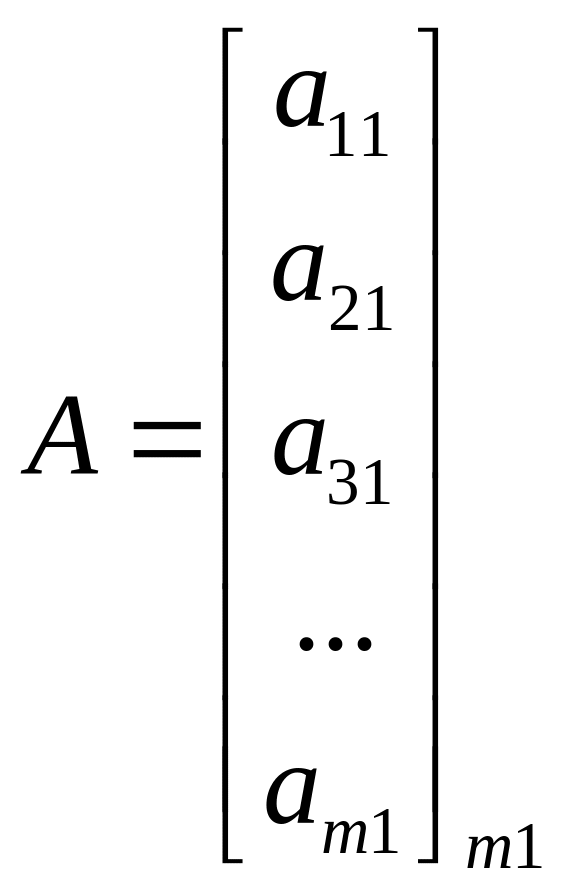Матрица нулевого порядка смысла не имеет.

Квадратная матрица, у которой диагональные элементы не равны нулю, а все недиагональные элементы равны нулю, называются диагональной

.

Диагональная матрица, у которой все ненулевые элементы равны единице, называется единичной и обозначается

.

Матрица, все элементы которой равны нулю, называется нулевой и обозначается

.

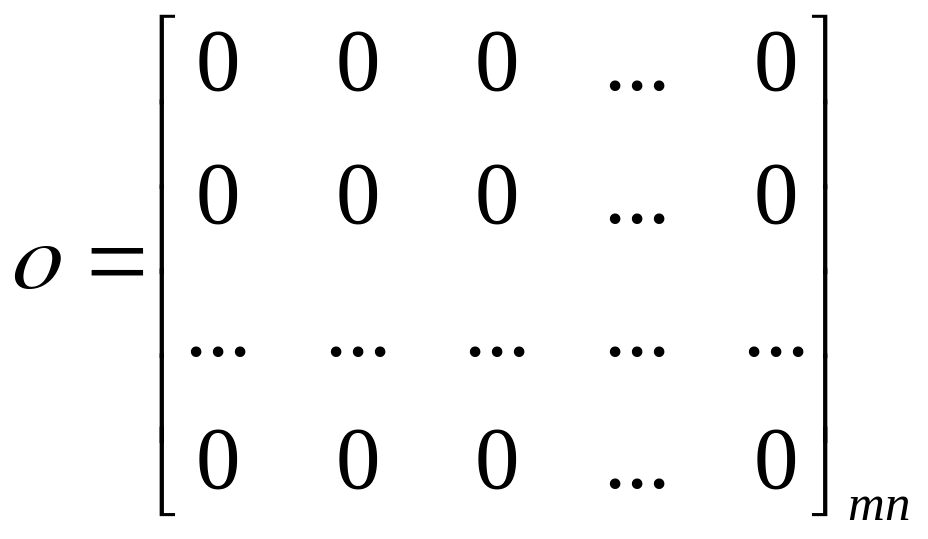1.1.2. Определитель

Определитель (или детерминант) является важной числовой характеристикой квадратной матрицы ∆, обозначается или det A и вычисляется по известным правилам. Классический способ вычисления (первый способ)

,

где:	– произвольная перестановка вторых индексов; – число беспорядков в перестановке вторых индексов.

Число слагаемых произведений равно числу возможных перестановок вторых индексов, т.е. равно n!, где – порядок квадратной матрицы.

Пример:

, _.

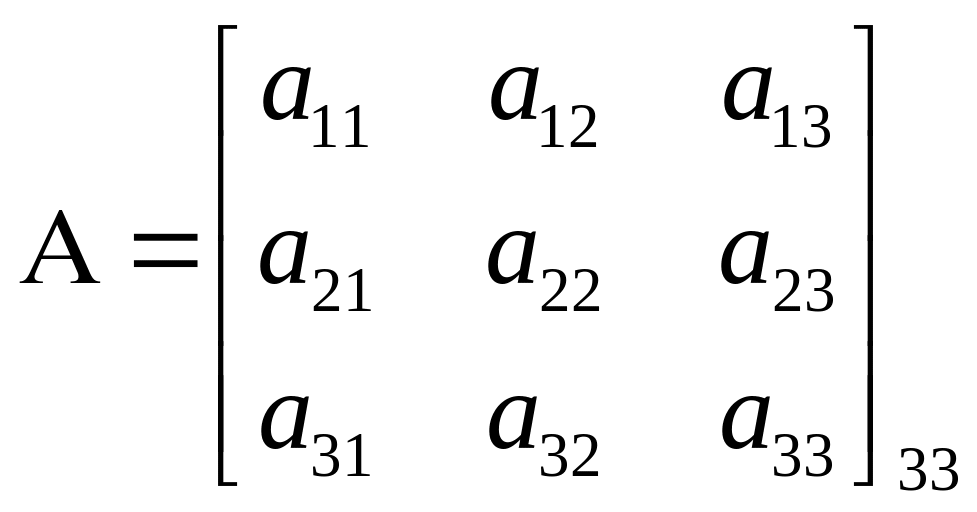Слагаемые произведения	Возможные перестановки вторых индексов	Число беспорядков

;

.

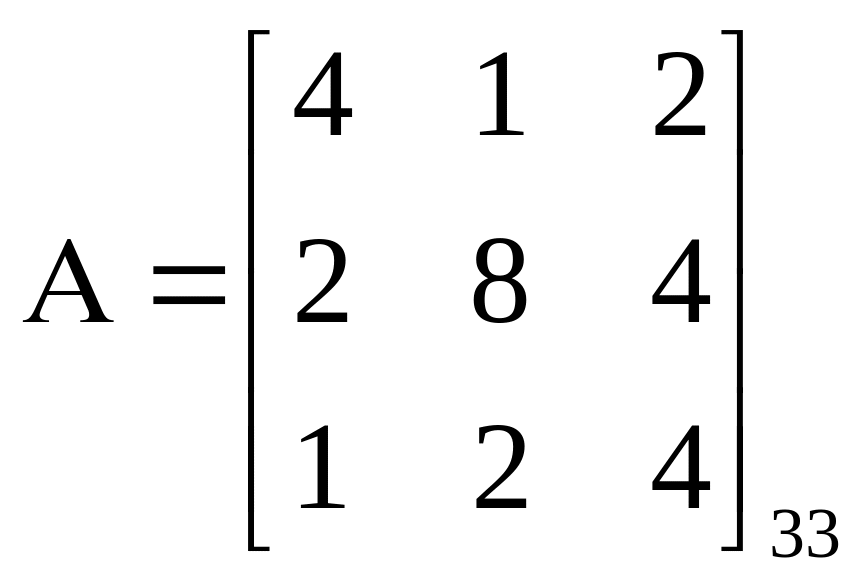Число слагаемых произведений при вычислении Δ возрастает стремительно с увеличением n:

n = 2 2! = 2

n = 3 3! = 6

n = 4 4! = 24

n = 5 5! = 120

n = 6 6! = 720

Вычислять Δ классическим способом сложно и поэтому применяют другие способы.

Вычисление Δ матрицы второго порядка ( ).

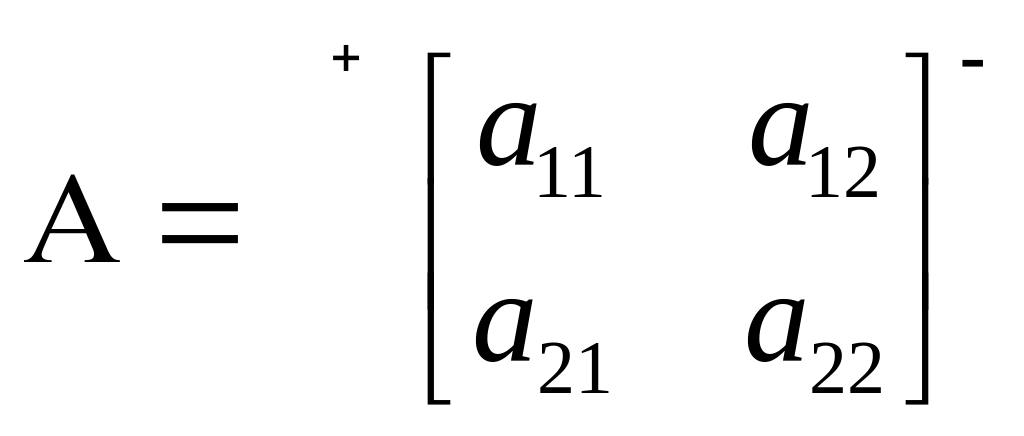
Два частных способа вычисления Δ для матриц только третьего порядка ( ).

Первый способ:

	Слагаемые произведения со знаком +
	Слагаемые произведения со знаком -

Указанные два способа вычисления Δ для матриц второго и третьего порядков основаны на использовании геометрического расположения элементов в матрицах, что неприменимо для матриц более высокого порядка.

1.1.3. Миноры и алгебраические дополнения

Минором М_ij элемента а_ij матрицы, называется определитель матрицы (n-1)-го порядка, полученной из матрицы А путем вычеркивания i-й строки и j-го столбца.

Алгебраическое дополнение А_ij равен минору, М_ij, если сумма (i+j) есть четное число и А_ij=-M_ij, если сумма (i+j) есть четное число, то есть

.

Универсальный способ вычисления определителя квадратных матриц любого порядка заключается в следующем: определитель квадратной матрицы А равен сумме произведений элементов любой строки (или любого столбца) на их алгебраические дополнения:

по i-й строке	,	где ;
по j-му столбцу	,	где .

Для квадратной матрицы третьего порядка

можно написать шесть выражений для вычисления определителя:

по трем строкам:	, , .
и трем столбцам:	, , .

Обычно для вычисления Δ данным способом выбирается строка или столбец, которые содержат больше нулевых элементов, чтобы уменьшить число слагаемых произведений. Согласно схеме вычислений определителя матрицы n-го порядка необходимо найти определители для матрицы (n-1)-го порядка. Очевидно, что для их нахождения в свою очередь можно использовать ту же схему вычислений и перейти к нахождению определителей матрицы (n-2)-го порядка. И так далее до тех пор, пока не дойдет до матрицы 3-го или 2-го порядка, для которых мы уже умеем вычислять определители.

Самый лучший способ вычисления определителя квадратной матрицы большой размерности (если элементы к тому же являются нецелыми числами), заключается в преобразовании квадратной матрицы к треугольному виду, т.е. к такому виду, когда у полученной после преобразования матрицы все элементы сверху или снизу главной диагонали являются нулевыми

.

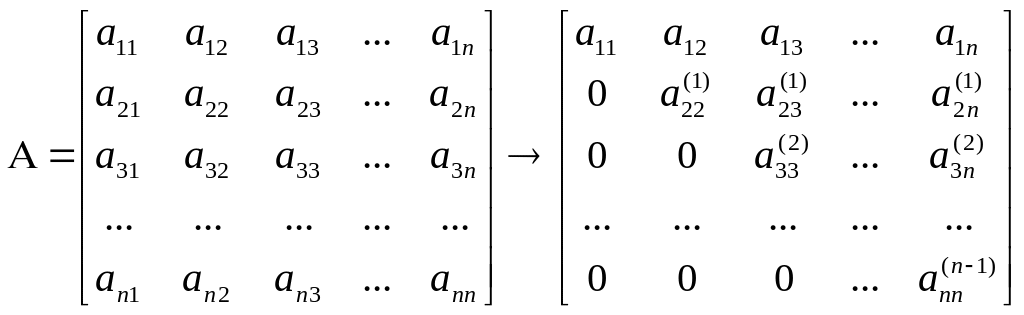Определитель квадратной матрицы А равен произведению диагональных элементов полученной в результате (n-1)-шагов преобразований треугольной матрицы

.

Преобразование квадратной матрицы к треугольному виду рассмотрим позднее («прямой ход» методом Гаусса).