Недостатки данного показателя:

1) Оторванность от других показателей. Это объясняется тем, что при построении показателя используется искусственный подход, т. Е. Отклонение берется по модулю (положительное);

2) Недостаточная реакция на слабые различия в степени вариации.

Дисперсия – это среднее арифметическое квадратов отклонения наблюдаемых значений признака от – их среднего значения x.

Если значения признака, полученные в результате выборочного наблюдения, не группировать и не представлять в виде вариационного ряда, то для вычисления дисперсии используют формулу:

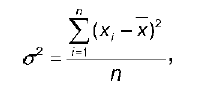
где n – объем выборки.

Среднеквадратическое отклонение – это квадратный корень из среднего арифметического квадратов отклонения наблюдаемых значений признака от – их среднего значения x, или квадратный корень из дисперсии.

Среднеквадратическое отклонение для несгруппированных данных рассчитывается по формуле:

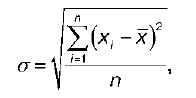
11. Относительные показатели вариации. Правило сложения дисперсий

Основной недостаток абсолютных показателей заключается в том, что они не позволяют сопоставлять между собой средние отклонения различных показателей. Для сопоставления необходимы относительные показатели, характеризующие относительную колеблемость. К ним относятся:

1)  коэффициент вариации. Рассчитывается как процентное отношение среднего квадратического отклонения к средней арифметической величине:

2)  коэффициент колеблемости. Рассчитывается как процентное отношение среднего абсолютного (линейного) отклонения к средней арифметической величине:

3)  коэффициент асциляции. Рассчитывается как отношение вариационного размаха к средней арифметической величине:

С помощью относительных показателей вариации решаются следующие задачи:

1) сравнение степени вариации в процентах различных признаков в одной и той же совокупности;

2) сравнение степени вариации одного и того же признака в различных совокупностях.

Правило или теорему сложения дисперсий сформулировал и доказал В. Лексис. В связи с тем что некоторые совокупности делятся на группы, помимо общей дисперсии, могут быть рассчитаны также дисперсии для каждой отдельной группы. Кроме этого, можно рассчитать среднюю из групповых дисперсий и межгрупповую дисперсию. В. Лексис доказал, что между данными показателями существует связь.

Теорема. Если совокупность состоит из нескольких групп, то общая дисперсия равна сумме внутри‑групповой и межгрупповой дисперсий:

где σобщ – общая дисперсия:

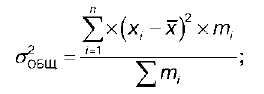
σвнгр – внутригрупповая дисперсия:

σгр – групповая дисперсия:

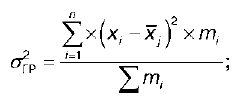
σмегр – межгрупповая дисперсия:

Если межгрупповая дисперсия равна нулю, то общая дисперсия равна средней из групповых дисперсий.

С помощью теоремы сложения дисперсий решаются следующие задачи :

1) Исследование зависимостей между признаками;

2) Оценка тесноты связи между признаками;

3) Оценка точности типичной выборки.

12. Понятие индексов. Классификация индексов

Индексный метод является одним из важнейших методов в статистике. Индексы относятся к числу обобщающих показателей. Следует различать понятие индекса в широком и узком смысле.

В широком смысле индекс – это относительная величина, характеризующая изменения явлений во времени (динамику). Но подобные относительные величины могут быть рассчитаны лишь для простых явлений или однородных совокупностей, единицы которых могут быть суммированы. Такие совокупности называются соизмеримыми.

Индекс в узком смысле слова – это обобщающий показатель сравнения двух совокупностей, состоящий из элементов, непосредственно не поддающихся суммированию.

С помощью индексов решаются две основные задачи:

1) синтетическая задача – обобщение, синтез дина мики отдельных элементов в сложные явления в од ном обобщающем показателе (сводном индексе);

2) аналитическая задача – анализ влияния изменения отдельных факторов на изменение сложного явления.

Классификация индексов по различным при знакам:

1) по степени охвата совокупности выделяют индивидуальные индексы (элементарные) и общие индексы (сводные или сложные);

2) по форме построения выделяют агрегатные, средневзвешенные (арифметические, гармонические) индексы;

3) по применяемым весам выделяют индивидуальные индексы с постоянными и переменными весами;

4) по состоянию явления выделяют индексы переменного состава, постоянного состава, структурных сдвигов;

5) по содержанию индексируемых величин выделяют индексы цен, физического объема товарооборота, себестоимости, трудоемкости и т. д.;

6) по базе сравнения выделяют динамические (базисные, цепные) индексы, индексы выполнения плана, планового задания, территориального сравнения.

Классификация показателей при построении индексов:

1)  количественные показатели, характеризующие объем того или иного явления.

К ним относятся:

а) q – физический объем товарооборота (количество проданной продукции в натуральном выражении);

б) q – физический объем продукции (количество произведенной продукции на предприятии);

в) t – число рабочих;

г) h – посевная площадь и др. Количественные показатели получают путем подсчета;

2)  качественные показатели характеризуют уровень явления в расчете на ту или иную единицу совокупности.

К ним относятся:

а) р – цена единицы товара (себестоимость);

б) z – себестоимость единицы продукции (затраты на производство единицы продукции);

в) t – трудоемкость единицы продукции (затраты рабочего времени на производство единицы продукции);

г) w – производительность труда (выработка продукции в единицу времени);

д) у – урожайность;

3)  суммарные (итоговые, количественно‑качественные) показатели, характеризующие суммарные, общие размеры исследуемого явления.

К ним относятся:

а) S – товарооборот:

S = p × q ;

б) Т – затраты рабочего времени (труда) на производство всей продукции:

Т = t × q ;

в) С – затраты на производство продукции:

С = z × q ;

г)  V – валовой сбор с/х культур по видам:

V = y × n .