27. Нормальная линейная модель парной регрессии
При построении нормальной (классической) линейной модели парной регрессии, т. е. модели регрессии с одной факторной переменной, учитываются следующие условия :
1) хi (факторная переменная) является неслучайной (детерминированной) величиной, независящей от распределения случайной ошибки регрессионной модели εi;
2) математическое ожидание случайной ошибки регрессионной модели Е(εi) равно нулю во всех i наблюдениях, т. е. Е ( εi ) = 0 при i = 1,n;
3) дисперсия случайной ошибки регрессионной модели D( εi ) постоянна для всех наблюдений, т. е.:
D( εi ) = Е( εi ) = G2 = const;
4) случайные ошибки регрессионной модели не коррелированы между собой, т. е. ковариация случайных ошибок любых двух разных наблюдений равна нулю:
Cov ( ε i ε j) = E( ε i ε j) = 0, где i ≠ j .
Ковариацией называется показатель
тесноты связи между переменными:
где x y – среднее арифметическое значение произведения факторной и результативной переменных:
x – среднее арифметическое факторной переменной;
y – среднее арифметическое результативной переменной;
Четвертое условие выполняется в том случае, если
изучаемые данные не являются временными рядами;
5) исходя из третьего и четвертого условий, можно добавить пятое условие о том, что случайная ошибка регрессионной модели является случайной величиной, подчиняющейся нормальному закону распределения с нулевым математическим ожиданием и дисперсией G 2 : ε i ~N ( 0, G 2). На основании перечисленных условий нормальная линейная модель парной регрессии записывается следующим образом:
y i = в 0 + в 1 x i + ε i ,
где y i – значения результативной переменной; x i – значения факторной переменной;
в 0 , в 1 – неизвестные параметры модели парной регрессии;
ε i – случайная ошибка регрессионной модели;
n – количество наблюдений.
Нормальная линейная модель парной регрессии может быть также записана в матричном виде:
Y = βX + ε,
где Y – вектор значений результативной переменной размерности n × 1; X – вектор значений факторной переменной размерности n × 2. Первый столбец является единичным, т. к. в регрессионной модели параметр в 0 умножается на единицу;
β – вектор коэффициентов регрессионной модели размерности 2 × 1; n.
ε – вектор случайных ошибок регрессионной модели размерности n × 1 .
28. Классический метод наименьших квадратов для модели парной регрессии
Неизвестные параметры в 0 и в 1 нормальной линейной модели парной регрессии определяются с помощью классического метода наименьших квадратов, или МНК.
Предположим, что исследователем собран цифровой материал, характеризующий две переменные – х и у.
Связь между исследуемыми переменными описывается равенством вида:
yi = β 0+ β 1xi. (2)
В соответствии с методом наименьших
квадратов в качестве метода оценки
неизвестных параметров регрессионной
модели будет выступать сумма квадратов
отклонений наблюдаемых значений
результативного признака у от
теоретических значений у (рассчитанных
с помощью регрессионной модели):
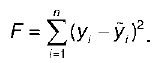
Для нахождения оптимальных значений неизвестных параметров β0 и β1 необходимо минимизировать функционал F по данным параметрам, т. е. необходимо рассчитать такие значения параметров β0 и β1, которые бы доставляли минимум функции:
При минимизации данного функционала неизвестными являются только значения коэффициентов регрессии β0 и β1. Значения результативной и факторной переменных известны из наблюдений.
Для определения минимума функции двух переменных нужно вычислить частные производные этой функции по каждому из оцениваемых параметров и приравнять их к нулю. Результатом будет являться стационарная система уравнений для функции (2):
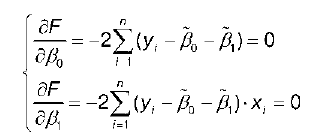
Если разделить обе части каждого уравнения системы на (‑2), раскрыть скобки и привести подобные члены, то получим систему:
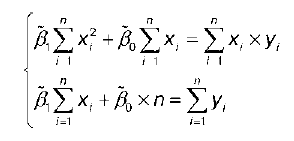
Решением системы нормальных уравнений являются оценки неизвестных параметров уравнения регрессии β0 и β1:
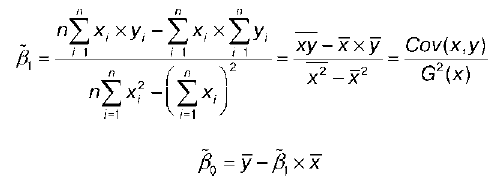
где у – среднее значение результативной переменной;
х – среднее значение факторной переменной;
ху– среднее арифметическое значение произведения результативной и факторной переменных;
G 2 (x) – дисперсия факторной переменной.