1) Определение формы корреляционной зависимости, т. Е. Вида функции регрессии (линейной, степенной и др.);
2) Оценка степени тесноты корреляционной связи между переменными либо на основе графика, либо на основе расчета специальных показателей тесноты связи.
24. Выборочный коэффициент корреляции
Выборочный коэффициент корреляции является одним из основных показателей тесноты связи между двумя переменными. При изучении зависимости переменной Y от переменной Х выборочный коэффициент корреляции обозначается как rxy. При изучении зависимости переменной Х от переменной Y выборочный коэффициент корреляции обозначается как ryx.
Выборочный коэффициент корреляции является оценкой коэффициента корреляции Pxy генеральной совокупности.
Выборочный парный коэффициент корреляции ryx:
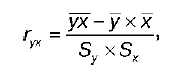
где ух – среднее арифметическое произведения факторной и результативной переменных:
S y – выборочное среднеквадратическое отклонение результативной переменной у , показывающее, на сколько единиц в среднем отклоняются значения результативной переменной у от ее среднего значения y–:
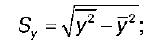
у 2 – среднее значение из квадратов значений результативной переменной у :
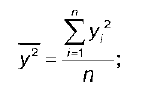
y2 – квадрат средних значений результативной переменной у :
S x – выборочное среднеквадратическое отклонение факторной переменной х, показывающее, на сколько единиц в среднем отклоняются значения факторной переменной х от ее среднего значения x :
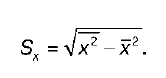
Выборочный коэффициент корреляции обладает следующими свойствами:
1) по абсолютной величине выборочный коэффициент корреляции не превосходит единицы: | r yx | ≤ 1, или –1 ≤ ryx ≤ 1;
2) если ryx = 0, т. е. выборочный коэффициент корреляции равен нулю, то переменные Y и Х не связаны статистической зависимостью. В этом случае проведение регрессионного анализа между исследуемыми переменными считается нецелесообразным;
3) если |ryx| = 1, т. е. выборочный коэффициент корреляции по абсолютной величине равен единице, то наблюдаемые значения исследуемых переменных связаны линейной функциональной зависимостью;
4) `если выборочный коэффициент корреляции принадлежит интервалу от нуля до единицы, то связь между исследуемыми переменными прямая; если же выборочный коэффициент корреляции принадлежит интервалу от нуля до минус единицы, то связь между исследуемыми переменными обратная.
25. Выборочное корреляционное отношение. Свойства выборочного корреляционного отношения
Выборочное корреляционное отношение является основным показателем при оценке тесноты нелинейной корреляционной связи между двумя переменными Y и Х. При изучении зависимости переменной Y от переменной Х выборочное корреляционное отношение обозначается как ηyx.
При изучении зависимости переменной Х от переменной Y выборочное корреляционное отношение обозначается как ηxy.
Выборочным корреляционным отношением
Y к Х называется отношение межгруппового среднего квадратического отклонения к общему среднему квадратическому отклонению переменной Y:
где Gмежгр – это межгрупповое среднее квадратическое отклонение переменной Y:
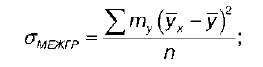
G общ – это общее среднее квадратическое отклонение переменной Y:
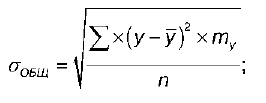
где n – объем выборки (сумма всех частот);
m х – частота значениях переменной X;
m – частота значения у переменной Y;
у – среднее значение переменной Y;
у х – условная средняя переменной Y.
Выборочным корреляционным отношением X
к Y называется отношение межгруппового среднего квадратического отклонения к общему среднему квадратическому отклонению переменной Х:
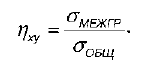
Выборочное корреляционное отношение обладает следующими свойствами: