17. Пропускная способность дискретного и непрерывного каналов связи

Непрерывного

Пусть сигнал   на выходе канала представляет собой сумму полезного сигнала   и шума  , т.е.  , причем   и   статистически независимы. Допустим, что канал имеет ограниченную полосу пропускания шириной  . Тогда в соответствии с теоремой Котельникова (см. п. 1.5) функции  ,   и   можно представить совокупностями отсчетов  ,  , и  ,  , где  . При этом статистические свойства сигнала   можно описать многомерной ПРВ  , а свойства шума – ПРВ  .

Пропускная способность непрерывного канала определяется следующим образом:

,

где      – количество информации о какой-либо реализации сигнала   длительности T, которое в среднем содержит реализация сигнала   той же длительности  , а максимум ищется по всем возможным распределениям .

Когда сигнал на входе канала имеет нормальное распределение и отсчеты независимы величина   максимизируется [6]. Поэтому пропускная способность гауссовского канала с дискретным временем, рассчитанная на единицу времени, с учетом (4.16) может быть записана в виде

.

(4.17)

Полученное выражение показывает, что пропускная способность гауссовского канала с дискретным временем определяется числом импульсов, передаваемых в секунду, и отношением сигнал/шум ( ).

С учетом взаимосвязи скорости передачи информации и полосы частот непрерывного канала от (4.17) можно перейти к формуле Шеннона, которая устанавливает связь пропускной способности гауссовского канала с полосой пропускания непрерывного канала и отношением мощности сигнала к мощности помехи:

.

(4.18)

График отношения   изображен на рис. 4.6. Заметим, что при малом отношении 

,

а пропускная способность канала связи прямо пропорциональна этому отношению.

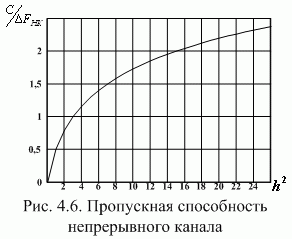
При большом отношении   в (4.18) можно пренебречь единицей и считать, что

,

т.е. зависимость пропускной способности непрерывного канала от отношения сигнал/шум логарифмическая.

Пропускная способность канала, как предельное значение скорости безошибочной передачи информации, является одной из основных характеристик любого канала.

Определим пропускную способность стандартного канала тональной частоты, имеющего границы эффективно передаваемых частот   кГц, среднюю мощность сигнала на выходе 56 мкВт при средней мощности помехи 69000 пВт.

Дискретного

Основной задачей систем связи является передача информации от источника к получателю. Решение этой задачи сопряжено с определенными трудностями, связанными не только с представлением информации в виде сообщения, пригодного для восприятия и обработки, но и с преобразованием данного сообщения в сигнал, пригодный для передачи по линии связи. Представим графически процесс передачи информации по каналу связи (рис.4.2) и учтем при этом возможное влияние помех.

Пусть дискретный канал определяется:

       – алфавитом источника сообщений;

        – алфавитом получателя сообщений;

        – «потерями» информации;

        – ложной информацией, создаваемой помехами;

 – количеством информации, переданной по каналу.

Условная энтропия характеризует среднюю степень неопределенности принимаемых сигналов, обусловленную действием помех.

При сопряжении входа канала с любым источником двоичной информации на вход могут поступать двоичные символы   и   с вероятностями   и   соответственно (рис.4.3). На выходе канала появляются двоичные символы   и  . Обозначим вероятность ошибки при передаче любого символа через  . Тогда,  , а  . В общем случае, для  -ичного дискретного канала [5]:

.

Тогда «шумовая» энтропия будет определяться выражением [5]:

(4.6)

Из полученного выражения следует, что энтропия определяемая только помехой не зависит от вероятности   появления символов на входе канала.

Если символы на входе канала выбираются независимо от предыдущих символов с одинаковыми вероятностями, то энтропия выходных символов достигает своего максимального значения, равного:  .

Таким образом, количество информации, переданной по каналу, это разность между энтропией на выходе и энтропией шума:

.

(4.7)

Количество информации, переданной по каналу связи, обладает следующими основными свойствами:

, причем   тогда и только тогда, когда входные и выходные сообщения в канале взаимно независимы;

, причем   тогда и только тогда, когда входная последовательность определяется однозначно по выходной последовательности, например, когда в канале нет помех;

 следует из того, что количество информации не изменится, если входную и выходную последовательность поменять местами.
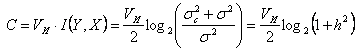