
- •Характерные особенности современных информационных систем. Основные определения. Задачи теории систем.
- •2. Краткая историческая справка. Терминология теории систем. Понятие информационной системы. Системный анализ.
- •3. Качественные и количественные методы описания информационных систем. Кибернетический подход. Динамические описание информационных систем.
- •5. Принципы минимальности информационных связей агрегатов. Агрегат как случайный процесс.
- •6. Анализ и синтез информационных систем. Формализация результатов изучения систем. Выделение функций систем.
- •7. Методология постановок и алгоритмизация задач задач на макро-и микро-уровнях.
- •8. Методы синтеза структур информационных систем. Задача оптимизации структур. Интеллектуализация информационных систем.
- •9. Информационные процессы-основа информационных систем.
- •10. Понятие и структура информационного процесса.
- •11. Математические модели сигнала.
- •12. Частотная форма представления детерминированных сигналов.
- •13. Классификация методов дискретизации. Дискретизация по времени.
- •14. Выбор точности отсчетов по теореме Котельникова. Квантование по уровню.
- •2. Виды импульсной модуляции.
- •3. Импульсные и цифровые методы в системах автоматического управления
- •15. Модели процесса. Измерение информации.
- •16. Модель непрерывного и дискретного каналов связи.
- •17. Пропускная способность дискретного и непрерывного каналов связи
- •18. Оценки потерь информации. Понятие избыточности информации.
- •19. Рассмотрение информационного процесса на физическом уровне. Назначение и содержание процедур модуляции и демодуляции.
- •Гармоническая модуляция
- •3. Импульсная модуляция
- •4. Широтно-импульсная модуляция
- •5. Дискретная модуляция
- •20. Сравнительные характеристики по помехоустойчивости различных видов модуляции.
- •21. Цифровые методы модуляции. Информационные характеристики сигнала и канала.
- •Цифровая модуляция
- •22. Согласование статистических свойств источника сообщений и канала связи.
- •23. Сети передачи данных. Пропускная способность сети связи.
- •24. Методы решения задачи статистической маршрутизации. Рассмотрение информационного процесса на канальном уровне.
- •Связь между офисами на канальном уровне
- •Проблема шифрования на сетевом уровне
- •Детальное рассмотрение прозрачного шифратора
- •Аналогии с режимами шифрования блочных шифров
- •25. Общие понятия теории кодирования. Фундаментальные теоремы Шеннона о кодировании.
14. Выбор точности отсчетов по теореме Котельникова. Квантование по уровню.
Выбор точности отсчетов по теореме Котельникова
Эта фундаментальная теорема показывает, что, если рассматриваемый сигнал ограничен некоторой частотой F сверху, то он может быть дискретизирован, то есть представлен дискретными измерениями с шагом во времени 2/F (полупериод граничной частоты), при этом дискретные измерения через 2/F несут без потерь всю информацию о сигнале.
В западной литературе совершенно бессовестно, в угоду принижения достижений СССР и России, а также в угоду прославления непричастных, но своих, ложно указывается, что данная теорема доказана, якобы, Шенноном и Найквистом. Когда же невозможно назвать ее ложным именем "теорема Найквиста - Шеннона", например, в русскоязычной литературе, то ее "скромно" называют "теоремой отсчетов".
Совершенно непонятна позиция некоторый российских писателей и лекторов, которые называют ее теоремой Шеннона - Котельникова. Из компромиса? - Разве может быть компромис между истиной и ложью?
На самом деле в 1933 году, когда эта теорема была опубликована В.А. Котельниковым в его работе "О пропускной способности эфира и проволоки в электросвязи", Шеннону было 17 лет. В тот год Клод Шеннон (1916 г.р.) только окончил среднюю школу и поступил работать курьером-разносчиком в один из офисов в своем городе, а о теории информации еще слухом не слыхивал.
В трудах Найквиста до сих пор не найдено доказательство этой теоремы, но лишь рассуждения вокруг этой темы. Однако рассуждения на тему и доказательство теоремы - разные вещи.
Правило
выбора предельного шага при равномерной
дискретизации с использованием модели
сигнала с ограниченным спектром
сформулировано, доказано и опубликовано
в 1933 году В. А. Котельниковым: «Любая
непрерывная функция s(t),
спектр которой ограничен
частотой Fmax полностью
определяется последовательностью
своих значений в моменты времени,
отстоящие друг от друга на интервал ![]() »
Кроме того, теорема Котельникова дает
и способ точного восстановления
сигнала
»
Кроме того, теорема Котельникова дает
и способ точного восстановления
сигнала ![]() по
его отсчетам.
по
его отсчетам.
Доказательство
 причем
причем ![]() при
при ![]() (1)
(1)
Разложим
функцию ![]() в
частотной области на конечном
интервале
в
частотной области на конечном
интервале ![]() (с
периодом
(с
периодом ![]() )
в комплексный ряд Фурье :
)
в комплексный ряд Фурье :
![]() где
(2)
где
(2)
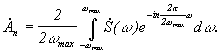 (3)
(3)
Сравнивая
интегралы в (3) и (1), видно, что они равны
при ![]() ,
т. е.
,
т. е. 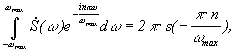 тогда
тогда
![]() (4)
(4)
Подставляем (4) в (2), а затем в (1)
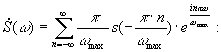
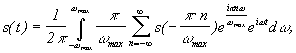
т. к. суммирование по от -¥ до +¥, то можно заменить знак у .
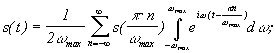
![]()
![]() (5)
(5)
Максимальные
значения членов ряда будут при ![]() и
равны
и
равны ![]() ,
при этом все остальные члены ряда равны
нулю, т. е. при
функция s(t) точно
передается рядом. Во все другие моменты
времени необходимо суммировать
бесконечное число отсчетов, чтобы
передать s(t) точно.
,
при этом все остальные члены ряда равны
нулю, т. е. при
функция s(t) точно
передается рядом. Во все другие моменты
времени необходимо суммировать
бесконечное число отсчетов, чтобы
передать s(t) точно.
Квантование по уровню
В
непрерывных автоматических системах,
изучавшихся в курсе "Основы ТАУ",
сигналы, поступающие на входы и выходы
элементов САУ, являются, как правило,
непрерывными функциями времени.
Однако во многих случаях оказывается
выгодным переход от непрерывного к
дискретному способу представления и
преобразования информации. Этот переход
осуществляется дискретизацией
непрерывного сигнала, т.е. заменой
непрерывной функций f(t) дискретными
значениями f1 ,f2,...,fn,
.. . Дискретизация (квантование)
непрерывного сигнала может осуществляться
по времени, по уровню или и по времени
и по уровню.
Дискретизация
сигнала по времени состоит в замене
непрерывного сигнала (рис.1,а)
дискретными значениями, взятыми в
определенные, заранее заданные моменты
времени. Обычно эти момента времени
равноудалены друг от друга на величину
Т , которая называется интервалом
квантования или периодом дискретности
(рис.1,б). В этом случае последовательность
{fn},
n=1,2,3... , определяется
формулой![]() Р
Р
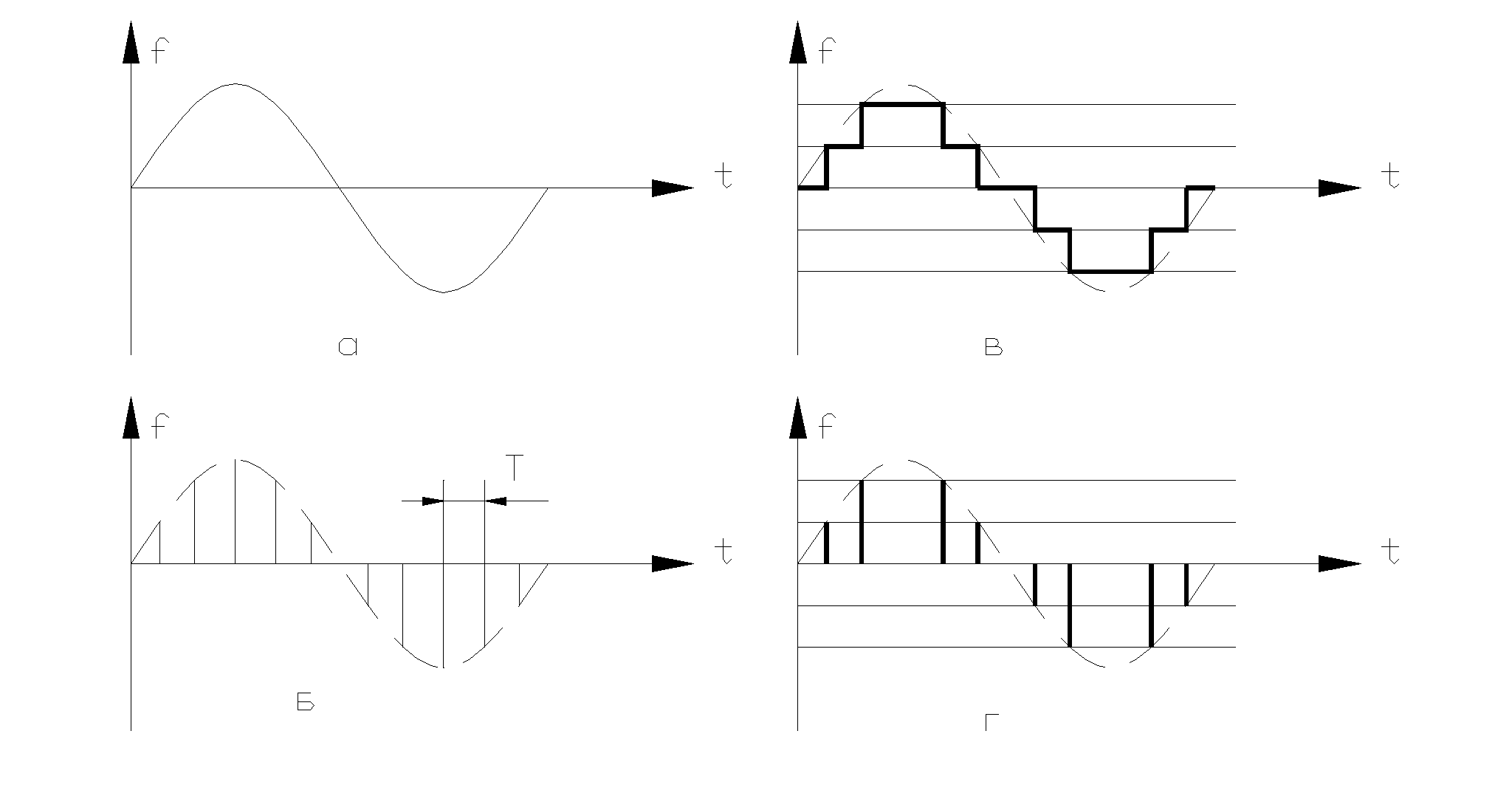 ис.1
Дискретизация
по уровню предполагает замену
непрерывного сигнала числовой
последовательностью f1 ,
f2,..,
fn,...,
элементы которой могут принимать
лишь заранее определенные , обычно
равноотстоящие друг от друга значения
(рис.1, в). Моменты времени, в которые
происходит смена уровней, определяются
видом непрерывного сигнала f(t) и заранее
неизвестны.
Дискретизация
и по времени и по уровню совмещает в
себе изложенные выше два способа
формирования последовательности
{fn},n=1,2..
. При этом непрерывный сигнал заменяется
дискретной последовательностью {fn},
n=1,2… взятой в заранее заданные моменты
времени, и каждый элемент этой
последовательности округляется до
ближайшего к нему значения уровня из
числа разрешенных (рис.1,г).
Обычно
применяют следующую классификацию
дискретных систем:
-
импульсные системы, в которых
осуществляется дискретизация хотя
бы одной из переменных системы по
времени;
-
релейные системы, в которых осуществляется
дискретизация по уровню;
-
цифровые системы, в которых осуществляется
дискретизация сигналов и по времени
и по уровню.
Из
приведенных трех типов дискретных
систем релейные САУ обычно рассматриваются
как непрерывные системы с разрывной
нелинейностью. В данном курсе ограничимся
изучением импульсных и цифровых
систем, особенности динамики которых
определяются дискретизацией по
времени.
^
ис.1
Дискретизация
по уровню предполагает замену
непрерывного сигнала числовой
последовательностью f1 ,
f2,..,
fn,...,
элементы которой могут принимать
лишь заранее определенные , обычно
равноотстоящие друг от друга значения
(рис.1, в). Моменты времени, в которые
происходит смена уровней, определяются
видом непрерывного сигнала f(t) и заранее
неизвестны.
Дискретизация
и по времени и по уровню совмещает в
себе изложенные выше два способа
формирования последовательности
{fn},n=1,2..
. При этом непрерывный сигнал заменяется
дискретной последовательностью {fn},
n=1,2… взятой в заранее заданные моменты
времени, и каждый элемент этой
последовательности округляется до
ближайшего к нему значения уровня из
числа разрешенных (рис.1,г).
Обычно
применяют следующую классификацию
дискретных систем:
-
импульсные системы, в которых
осуществляется дискретизация хотя
бы одной из переменных системы по
времени;
-
релейные системы, в которых осуществляется
дискретизация по уровню;
-
цифровые системы, в которых осуществляется
дискретизация сигналов и по времени
и по уровню.
Из
приведенных трех типов дискретных
систем релейные САУ обычно рассматриваются
как непрерывные системы с разрывной
нелинейностью. В данном курсе ограничимся
изучением импульсных и цифровых
систем, особенности динамики которых
определяются дискретизацией по
времени.
^
