МИНИСТЕРСТВО ОБРАЗОВАНИЯ и НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

Российский государственный университет туризма и сервиса

Филиал, г. Самара

В.М. Дуплякин контролируемая самостоятельная работа № 2

ПО КУРСУ МАТЕМАТИЧЕСКИХ МЕТОДОВ ОПТИМИЗАЦИИ РЕШЕНИЙ

ЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ

Методические указания студентам дневной формы обучения

Самара - 2014

КСР №2

Линейное программирование

Постановка задачи: Коммерческая фирма планирует закупку товаров двух видов с целью получения при последующей их реализации максимального объёма денежных поступлений. Каждая единица товара оформляется индивидуально.

Исходные данные для отдельной единицы товара:

продажная цена одной единицы первого и второго товара, ус.ед.;

складская площадь для хранения единицы первого и второго товара, м²;

трудоёмкость оформления одной единицы первого и второго товара, ус.ед.

Объём закупок имеет ограничения:

1. Общая площадь складского помещения для хранения товара .

2. Общая трудоёмкость оформления покупки, доставки, складирования и предпродажной подготовки .

Требуется определить:

1. Оптимальное число единиц каждого товара: .

2. Направление получения наибольшего объёма денежных поступлений в координатах .

3. Максимальный объём денежных поступлений от продажи всех закупленных товаров: .

4. Максимальное возможное число единиц каждого товара при их раздельной продаже: .

5. Объёмы денежных поступлений при торговле отдельно каждого из товаров: .

6. Для оптимального набора товаров следует проверить использование склада и трудовых ресурсов.

Решение выполняется графически и аналитически.

Постановка задачи линейного программирования

Целевая функция – суммарная выручка от продажи закупленных товаров .

Критерий оптимизации – максимизация выручки .

Рабочие переменные – число единиц закупаемых товаров .

Ограничения :

1. Методика решения

Рассматриваемая задача относится к простейшим задачам линейного программирования.

Поскольку в этой задаче только две независимые переменные , то она допускает наглядную геометрическую интерпретацию. В данной работе эту задачу необходимо решить и графически и аналитически.

Сначала на графике с координатами построим, как это показано, например, на рис. 1 , линию ограничений по объёму складских помещений АВ, которая описывается уравнением

(1)

Затем построим линию ограничений по трудоёмкости оформления, складирования и предпродажной подготовки товаров CD, которая задаётся уравнением

(2)

Областью возможных решений задачи для исходных данных соответствующих ограничениям представленным на рис. 1 является внутренняя часть многоугольника ОСРВ. Оптимальные решения могут находиться в точках С, Р, В.

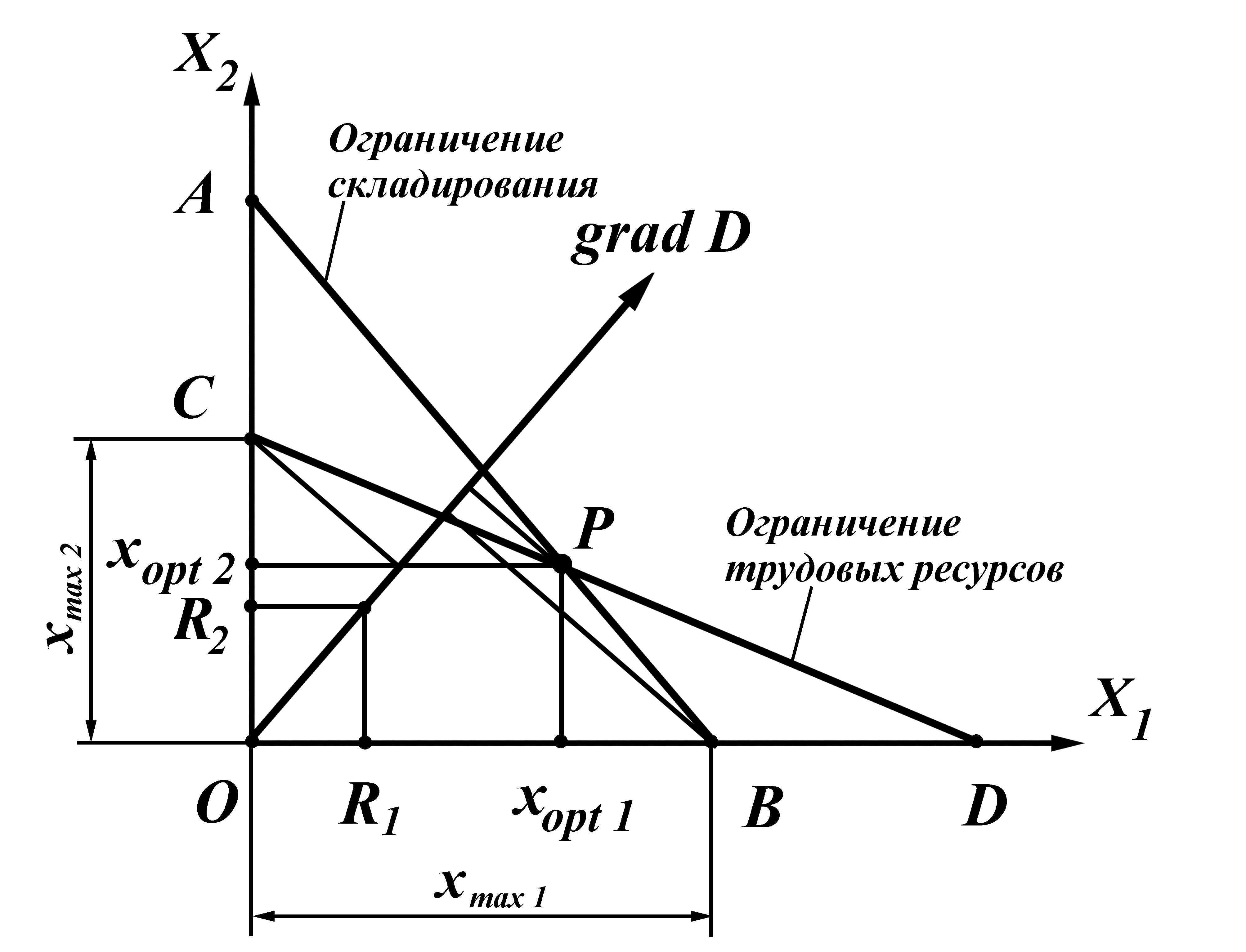
Рис. 1. Иллюстрация решения задачи линейного программирования

Абсцисса точки В представляет собой максимально возможное при данных ограничениях количество первого товара . Очевидно, что для данного товара определяющим будет ограничение по площадям складирования. Объём денежных поступлений от продажи максимально возможной партии первого товара определяется по формуле

Ордината точки С представляет собой максимально возможное при данных ограничениях количество второго товара . Для этого товара определяющим будет ограничение по трудоёмкости его оформления. Объём денежных поступлений от продажи максимально возможной партии второго товара определяется по формуле

Решение системы уравнений (1) и (2) даёт координаты точки Р, которая является точкой одновременного и полного исчерпания ограничений по складским площадям и по трудовым ресурсам. Координаты точки Р необходимо получить аналитически, а графическое решение использовать как средство иллюстрации и контроля.

Далее необходимо выяснить какая из рассмотренных точек на границе области возможных значений является решением данной задачи. Дело в том, что при сочетании исходных данных приводящем к более крутому наклону линии АВ по сравнению с наклоном линии CD, как это показано на рис. 1, оптимальным решением могут быть точки Р, С или D. В других случаях это могут быть точки Р, А или В.

Оптимальным будет то решение, которое находится дальше от начала координат , если это расстояние откладывается в направлении наибольшего возрастания целевой функции, которой в данном случае является функция, описывающая объём денежных поступлений при полной продаже закупленных товаров

где число единиц каждого из двух видов продаваемых товаров.

Градиент функции объёма денежных поступлений , т.е. направление наибольшего роста суммы денежных поступлений определяется как

В нашем случае (линейная зависимость денежных поступлений от объёма продаж) имеем

Построим на рис. 1 линию наибольшего изменения объёма денежных поступлений от объёмов проданных товаров . Для построения линии в направлении градиента отложим на координатных осях проекции и найдём графически их геометрическую сумму, как показано на рис. 1.

Оптимальным будет решение, которое имеет наибольшую по длине проекцию на направление градиента. В случае, представленном на рисунке 1 это будет точка Р с координатами .

Соответствующий объём денежных поступлений определим по формуле

где округленные до целых значений координаты .

Полученное решение следует сопоставить с объёмами поступлений от продажи максимально возможного количества товаров каждого вида.