Выравнивание ряда

Для выравнивания ряда примем обозначение дат с нулем в середине, т.е. t*₂₀₀₇=–1, t*₂₀₀₈=1. Тогда коэффициенты параметров линейного тренда находятся из уравнений:

Составим таблицу:

Год	t	Y	t2	t*Y
2004	-5	13,5	25	-67,5
2005	-3	13	9	-39
2006	-1	13,46	1	-13,46
2007	1	13,6	1	13,6
2008	3	13,9	9	41,7
2009	5	15,3	25	76,5
Сумма:	0	82,76	70	11,84

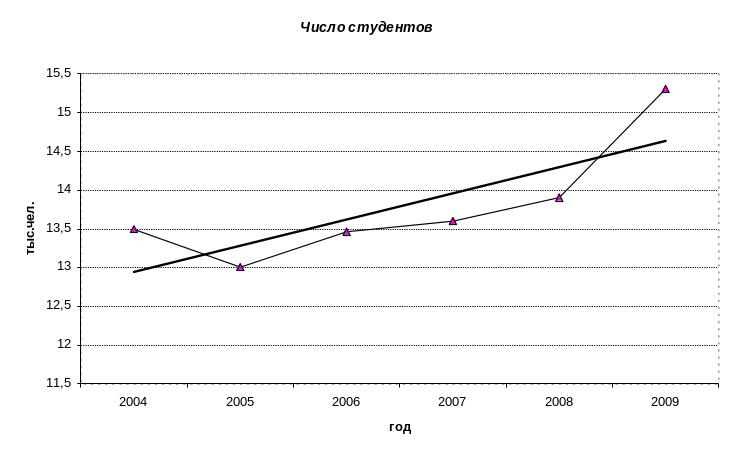
Уравнение выровненного ряда: Y=13,8 + 0,17·t

Уравнение выровненного ряда дано на Рис.1 утолщённой линией.

По этому уравнению можно спрогнозировать число студентов на 2013 год (t=13)

Y_t=13=13,8 + 0,17·13 = 16 тыс.чел.

По исходным данным построен график динамики числа студентов и выровненный ряд.

Выводы:

1. Показатели динамики характеризуют одним показателем общий характер развития исследуемого процесса во времени.

2. Наглядным и удобным представлением развития процесса являются статистические графики.

Вариант XXVIII Задача № 1. Себестоимость и объем продукции предприятия характеризуются следующими данными:

Изделие	Себестоимость единицы изделия, руб.		Выработано продукции, тыс. шт.
	Январь, z0	Февраль, z1	Январь, q0	Февраль, q1
1	220	240	130	160
2	170	185	100	180

Определите: 1) общий индекс затрат на все изделия; 2) общий индекс себестоимости единицы изделия; 3) общий индекс физического объема продукции. Сделайте выводы и покажите взаимосвязь индексов.

Решение:

1. общий индекс затрат на все изделия:

общий индекс себестоимости единицы изделия:

общий индекс физического объема продукции:

Связь индексов:

Вывод:

Таким образом, рост затрат на все изделия на 57% в основном связан с ростом физического объема продукции (на 44%).

Задача № 2. Имеются данные о численности работников и их заработной плате в вузах региона.

Специализация работников	Численность работников, чел.		Заработная плата, руб.
	базисный период, q0	отчетный период, q1	базисный период, p0	отчетный период, p1
Технические	520	510	15000	15900
Экономические	750	725	17800	18800

Определите: 1) среднюю заработную плату в целом за два периода; 2) изменение средней заработной платы: а) за счет изменения структуры работников; б) изменения заработной платы отдельных категорий работников. Покажите связь между исчисленными индексами. Сделайте выводы.

Решение:

1. Средняя заработная плата:

. Средняя заработная плата базисного периода: руб.

. Средняя заработная плата отчётного периода: руб.

средняя заработная плата в целом за два периода

руб.

Индекс заработной платы:

2) изменение средней заработной платы:

1. а) за счет изменения структуры работников: Индекс структурных сдвигов:

б) изменения заработной платы отдельных категорий работников:

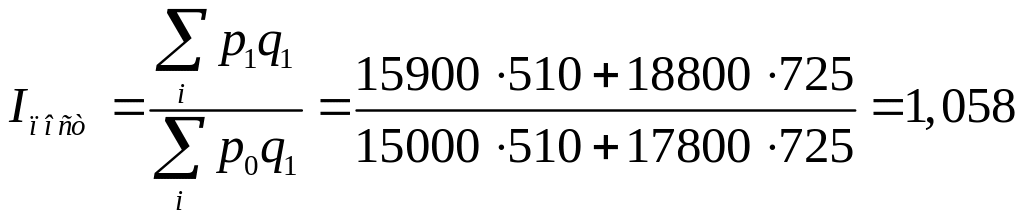
Вывод:

Таким образом, весь прирост средней заработной платы связан с ростом заработной платы каждой группы работников в отчётном периоде.