Контрольная работа

Контрольная работа состоит из трех задач, соответствующих изучаемым разделам курса. Варианты заданий соответствуют порядковому номеру студента в списке группы. Количество задач определяет преподаватель, ведущий дисциплину.

При оформлении контрольных работ необходимо придерживаться следующих рекомендаций.

1. Контрольная работа выполняется на стандартных листах формата А4 или в тетради.

2. Обложка оформляется в соответствии с образцом, приведенным в приложении.

3. Текст пишется от руки или с применением каких-либо технических средств.

4. В тексте записки недопустимы сокращения слов, кроме общепринятых (САУ, ТАУ и т. п.). При необходимости сокращения какого-либо наименования приводится соответствующее пояснение. Например: метод аналитического конструирования оптимальных регуляторов (АКОР).

5. Рисунки и графики включаются в записку по ходу текста.

6. Расчеты характеристик сводятся в таблицы.

7. Страницы, рисунки и таблицы должны быть пронумерованы.

8. Все действия должны сопровождаться соответствующими пояснениями.

9. Формулы вначале преобразуются в буквенном виде и только потом подставляются численные значения параметров и записывается конечный результат. Все обозначения в формулах следует расшифровать.

10. Список литературы приводится в конце расчетно-пояснительной записки.

Для каждого литературного источника указывается: фамилия И.О. автора, полное наименование, издательство, год издания и количество страниц.

На проверку контрольная работа представляется в сшитом виде. Зачет проводится устно в процессе собеседования с преподавателем.

Задача № 1

Задание: Для линейной импульсной САУ с экстраполятором нулевого порядка, заданной структурной схемой (рис. 1) и значениями параметров (табл. 1) (по вариантам).

1. Записать дискретные передаточные функции разомкнутой и замкнутой системы.

2. Найти характеристическое уравнение замкнутой САУ.

3. Определить устойчивость импульсной САУ по аналогам алгебраических критериев устойчивости.

4. Определить устойчивость импульсной САУ по аналогу критерия Михайлова.

5. Определить устойчивость заданной системы по логарифмическим частотным характеристикам.

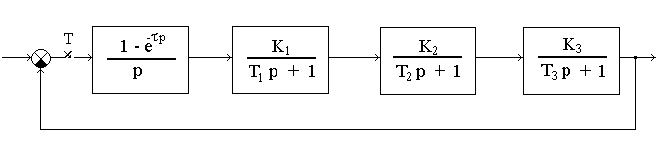
Рис. 1

Методические указания к выполнению задачи № 1

Дискретная передаточная функция разомкнутой линейной импульсной системы с экстраполятором нулевого порядка определяется по формуле:

,

где W_нч (P) – передаточная функция непрерывной части системы.

Уравнение, стоящее в фигурных скобах, необходимо представить в виде суммы простейших слагаемых:

,

найти значения A, B, C, D методом неопределенных коэффициентов и, воспользовавшись таблицей Z-преобразований, определить дискретную передаточную функцию W_p (Z).

Дискретная передаточная функция замкнутой системы рассчитывается по формуле:

.

Если знаменатель этой функции приравнять к нулю, то получим характеристическое уравнение замкнутой системы: a₀ Z³ + a₁ Z² + a₂ Z + a₃ = 0

Для оценки устойчивости линейной импульсной системы с помощью известных алгебраических критериев необходимо от Z-преобразований перейти к V-преобразованиям с помощью формулы: и по полученному характеристическому уравнению: A₀ V³ + A₁ V² + A₂ V + A₃ = 0 определить устойчивость системы по критерию Рауса или Гурвица.

Если в характеристическом уравнении (в Z – изображении) заменить Z на e ^jωΤ, то использовав формулу Эйлера: , можно выделить вещественную и мнимую составляющие функции Михайлова. Изменяя частоту от 0 до П/Т, рассчитываются соответствующие значения этих составляющих и строится годограф Михайлова, по которому можно сделать вывод об устойчивости импульсной САУ.

Для построения логарифмических частотных характеристик разомкнутой системы необходимо в передаточной функции Wp(Z) перейти к V – преобразованиям. При этом передаточная функция Wp(V) должна состоять из произведения передаточных функций типовых динамических звеньев. ЛАЧХ и ЛФЧХ разомкнутой системы строятся по известной методике.

Задача № 2

Рассчитать спектральную плотность ошибки замкнутой САУ с единичной отрицательной обратной связью при подаче на ее вход случайного сигнала типа "белый шум" со спектральной плотностью Sg (ω) = N, если передаточная функция разомкнутой системы имеет вид:

1.

2.

3.

4.

5.

6.

7.

8.

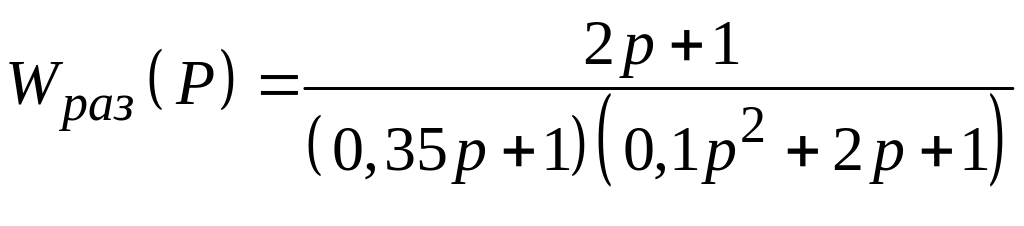
9.

10.

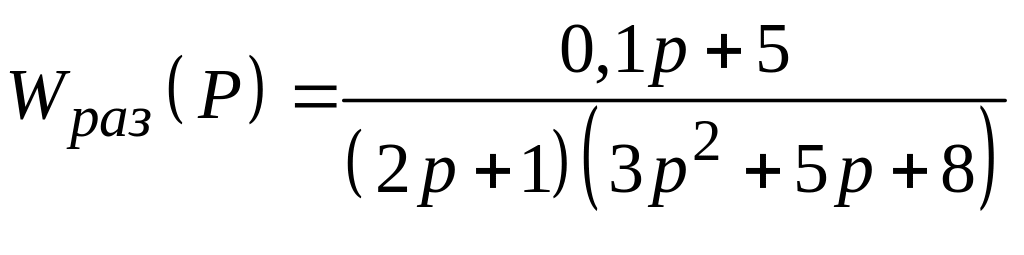
11.

12.

13.

14.

15.

16.

17.

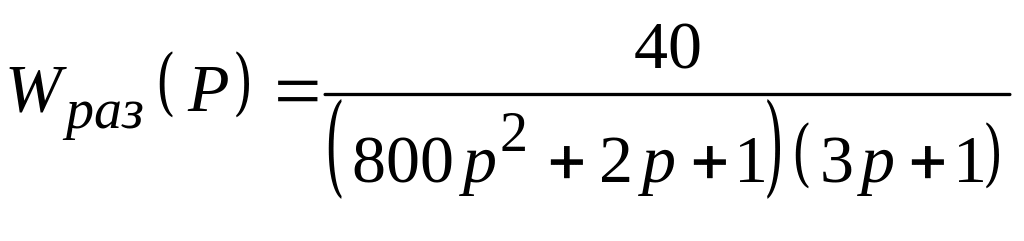
18.

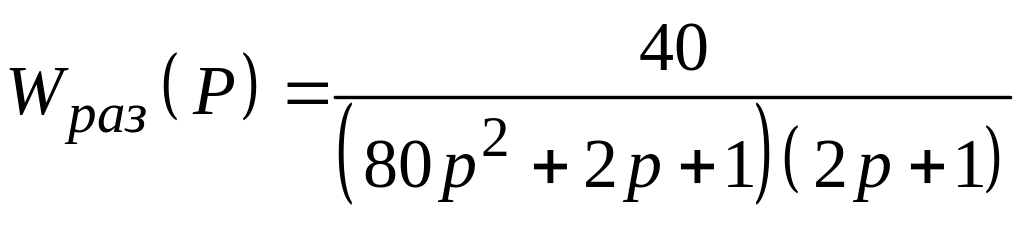
19.

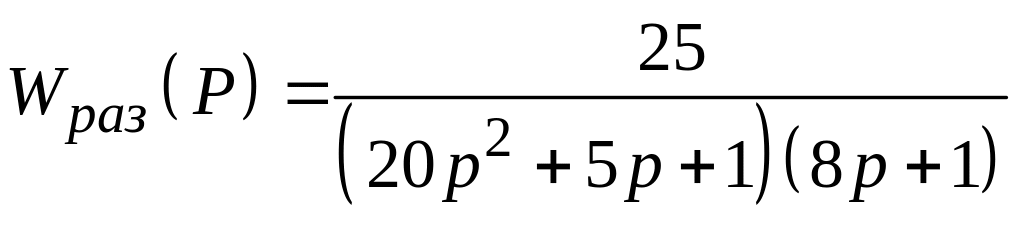
20.

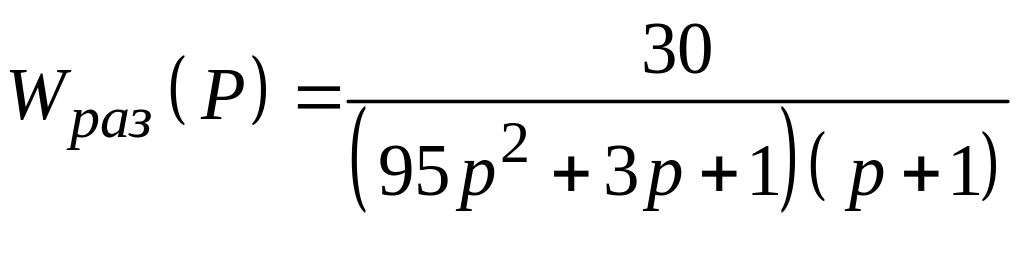
21.

22.

23.

24.

25.

26.

27.

28.

29.

30.

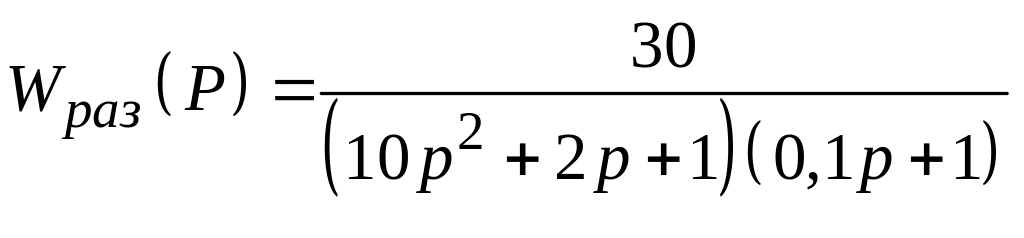
Методические указания к выполнению задачи № 2

Спектральная плотность ошибки замкнутой САУ при подаче на ее вход случайного сигнала рассчитывается по формуле: ,

где, – частотная функция замкнутой САУ по ошибке. Модуль данной функции определяется известным способом.

Задача № 3

Для электропривода постоянного тока с безынерционным тиристорным преобразователем требуется:

1. Определить закон оптимального по быстродействию управления на входе преобразователя, обеспечивающий перевод электропривода из начального состояния

_Δα (0) = _Δα₀, ω(0) = ω₀ = 0 в конечное положение _Δα (t) = 0 и ω (t) = 0 при наличии ограничения на управление преобразователем U_у ≤ U_{у max} = ± 10В. Здесь _Δα = α₃ – α (t) – ошибка по углу;

α₃ – требуемый угол перемещения.

2. Построить семейство фазовых троекторий при различных начальных условиях и оптимальном управлении U_опт (t).

3. Записать уравнение линии переключения управляющего воздействия как функцию скорости двигателя и ошибки по углу.

4. Составить структурную схему реализации оптимальной системы управления электроприводом по быстродействию.

Технические данные двигателя по вариантам приведены в табл. 2.

Методические указания к выполнению задачи № 3

При расчете заданного электропривода принять коэффициент усиления преобразователя

К_пр = 20. Сопротивление преобразователя следует считать равным сопротивлению якорной цепи электродвигателя. При решении задачи электромагнитной постепенной времени можно пренебречь. Задачу решать с помощью принципа максимума Понтрягина и метода фазовой плоскости.

Процесс решения задачи состоит из следующих этапов:

1. Записываются уравнения объекта управления в виде системы уравнений первого порядка, не забыв при этом уравнение для функционала: Y _i = f _i (U,Y, t)

2. Составляется функция Гамильтона:

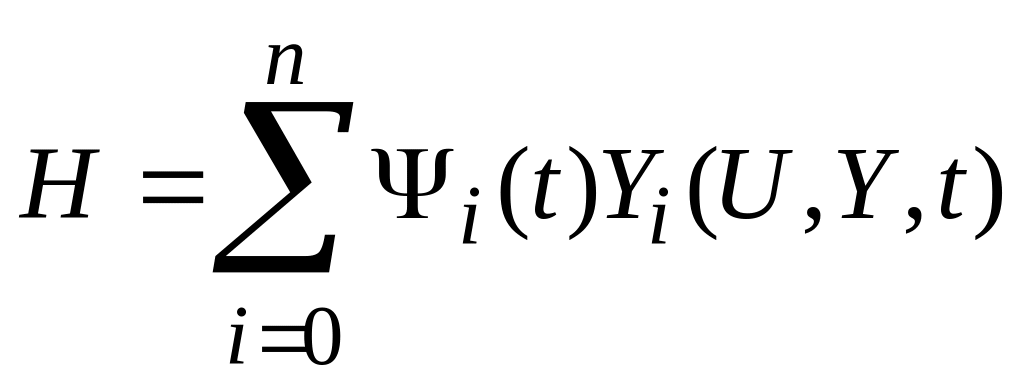
3. Определяется значение U, максимизирующие функцию Н,

4. Составляется уравнение для определения ψ_i (t)

(i = 1, 2, …, n)

Через функцию выражается искомое оптимальное управление.

Поскольку рассматривается вопрос оптимизации системы управления по быстродействию, то уравнение функционала имеет вид:

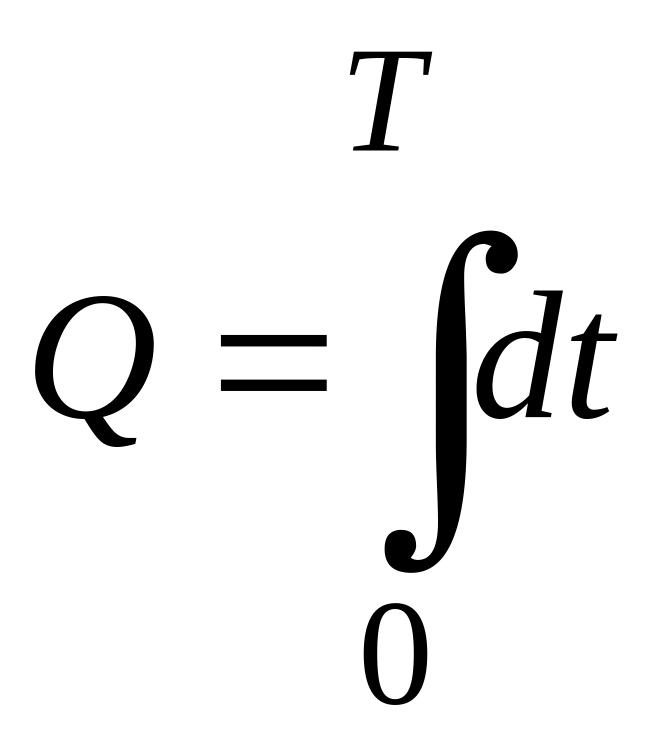
Так как в уравнение функционала не входит управление, то его не нужно включать в функцию Н.

Приложение

Образец оформления обложки контрольной работы

Новосибирский государственный технический университет

Кафедра ЭАПУ

Контрольная работа № 4

по Теории автоматического управления

вариант задания _______

студента ___ курса, группы _______ специальности ______________________

Ф.И.О. (полностью)

Домашний адрес _____________________________________________________

почтовый индекс, город (поселок)

улица, № дома, № квартиры

Работа выполнена ____________________________

дата

Работа защищена _____________________________

дата

Преподаватель _______________________________________________________

подпись Ф.И.О.

Таблица 1

Вариант	Значение параметров
	К1	К2	К3	Т1	Т2	Т3	Т
1	5	2	8	0,1	0,01	0,09	0,002
2	6	8	2	0,14	0,05	0,085	0,01
3	2	4	10	0,13	0,04	0,08	0,0025
4	3	3	9	0,1	0,02	0,075	0,002
5	10	2	4	0,16	0,01	0,07	0,002
6	5	6	3	0,15	0,03	0,065	0,003
7	4	3	7	0,15	0,01	0,05	0,002
8	4	10	2	0,1	0,02	0,055	0,002
9	2	10	4	0,1	0,02	0,06	0,002
10	1	10	8	0,2	0,05	0,065	0,003
11	8	6	2	0,26	0,04	0,07	0,005
12	7	5	2	0,25	0,03	0,075	0,002
13	6	8	2	0,24	0,02	0,08	0,003
14	5	2	8	0,3	0,01	0,085	0,004
15	8	3	3	0,2	0,02	0,09	0,002
16	3	9	3	0,2	0,03	0,095	0,0025
17	2	9	4	0,1	0,04	0,15	0,003
18	8	5	2	0,12	0,045	0,2	0,0035
19	2	6	8	0,13	0,05	0,25	0,002
20	4	10	2	0,14	0,055	0,2	0,004
21	9	3	3	0,15	0,06	0,3	0,0015
22	6	5	3	0,16	0,045	0,09	0,003
23	7	4	3	0,17	0,04	0,08	0,004
24	10	4	2	0,18	0,035	0,07	0,003
25	8	1	10	0,2	0,03	0,06	0,005
26	2	6	8	0,21	0,025	0,05	0,004
27	8	2	5	0,22	0,02	0,055	0,002
28	6	4	3	0,23	0,028	0,07	0,003
29	5	6	3	0,24	0,032	0,09	0,004
30	9	8	1	0,25	0,044	0,1	0,005

Таблица 2

№ в-та	Тип двигателя	Рн, кВт	Uн, В	nн об/мин	КПД, %	Rяц, Ом	J, кгм2	αз, град	Т, с
1	2ПБ-112L	1,5	220	2240	80	1,48	0,018	400	2,5
2	2ПБ-112L	2	220	3150	81	0,824	0,018	425	2
3	2ПН-132M	1,6	220	750	68,5	3,27	0,038	450	2
4	2ПН-132M	2,5	220	1000	73,5	1,843	0,038	480	1
5	2ПН-132M	4	220	1500	7,9	0,9	0,038	280	3
6	2ПН-132L	1,9	220	750	72	2,28	0,048	250	4
7	2ПН-132L	3	220	1000	75,5	1,52	0,048	500	3,5
8	2ПН-132L	5,5	220	1500	80,5	0,592	0,048	520	3
9	2ПБ-132L	1,1	220	800	67	3,97	0,038	550	3
10	2ПБ-132L	1,6	220	1000	70,5	2,38	0,038	600	1
11	2ПБ-132M	2,4	220	1600	77	1,226	0,038	700	1,5
12	2ПБ-132M	3,7	220	2360	81	0,57	0,038	650	2,5
13	2ПБ-132M	1,5	220	3150	81,5	0,333	0,038	750	3,5
14	2ПБ-132L	1,3	220	800	72	0,708	0,048	800	2,5
15	2ПБ-132L	1,9	220	1060	76,5	1,995	0,048	830	3
16	2ПБ-132L	3,2	220	1600	82,5	0,841	0,048	850	2
17	2ПБ-132L	4,5	220	2200	84	0,489	0,048	900	2,5
18	2ПБ-132L	5,3	220	3000	85,5	0,291	0,048	950	1
19	2ПО-132L	1,8	220	1000	64,5	2,38	0,038	1500	1,5
20	2ПО-132L	2,8	220	1500	76,5	1,055	0,038	1530	3,5
21	2ПО-132M	4,5	220	2240	81	0,475	0,038	1350	4
22	2ПО-132L	1,6	220	750	71	2,63	0,048	1400	4,5
23	2ПО-132L	2,2	220	1000	75,5	1,52	0,048	900	3,5
24	2ПО-132L	3,4	220	1600	81	0,708	0,048	930	3
25	2ПФ-132M	2	220	750	67	2,953	0,038	700	3,5
26	2ПФ-132L	3	220	1060	74	1,598	0,038	720	2
27	2ПФ-132M	4	220	1500	80,5	0,78	0,038	750	2,5
28	2ПН-160M	3	220	750	76,5	1,217	0,038	250	3,5
29	2ПН-160M	4,5	220	1000	79,5	0,715	0,038	270	5
30	2ПН-160L	4	220	800	78,5	0,875	0,1	300	5,5

Примечание: Число пар полюсов для всех электродвигателей, приведенных в таблице 2, равно 2.

33