1. Охарактеризуйте составные части эконометрической модели.

Эконометрическая модель (econometric model) - это статистическая модель, которая является средством прогнозирования значений определенных переменных- эндогенных, используются значения других переменных, называемых экзогенными.

Эконометрическая модель имеет следующий вид[3]:

Y=f(X) + е

где Y - наблюдаемое значение переменной (объясняемая переменная);

f(X) - объясненная часть, зависящая от значений объясняющих переменных;

X={x1,x2,…,xn}

е - случайная составляющая (возмущения).

2. Какие гипотезы проверяются с помощью критерия Стьюдента?

Предположим, что по данным выборочной совокупности была построена линейная модель парной регрессии. Задача состоит в проверке значимости парного коэффициента корреляции между результативной переменной у и факторной переменной х. Основная гипотеза состоит в предположении о незначимости парного коэффициента корреляции, т. е.

Н0:rxy=0.

Обратная или конкурирующая гипотеза состоит в предположении о значимости парного коэффициента корреляции, т. е.

Н1:rxy≠0.

Данные гипотезы проверяются с помощью t-критерия Стьюдента.

3. Что показывает коэффициент корреляции?

(Коэффициент корреляции показывает степень статистической зависимости между двумя числовыми переменными. Он вычисляется следующим образом:

,

где n – количество наблюдений, x – входная переменная, y – выходная переменная. Значения коэффициента корреляции всегда расположены в диапазоне от -1 до 1

Коэффициент корреляции равен квадратному корню коэффициента детерминации, поэтому может применяться для оценки значимости регрессионных моделей.

4. Какие гипотезы проверяются с помощью критерия Фишера?

Проверка значимости коэффициентов регрессии означает проверку основной гипотезы об их значимом отличии от нуля.

Основная гипотеза состоит в предположении о незначимости коэффициентов модели множественной регрессии, т. е.

Обратная или конкурирующая гипотеза состоит в предположении о значимости коэффициентов модели множественной регрессии, т. е.

Данные гипотезы проверяются с помощью t-критерия Стьюдента, который вычисляется посредством частного F-критерия Фишера-Снедекора.

5. Что показывает коэффициент детерминации?

Коэффициент детерминации (  — R-квадрат) — это доля дисперсии зависимой переменной, объясняемая рассматриваемой моделью зависимости, то есть объясняющими переменными. Более точно — это единица минус доля необъяснённой дисперсии (дисперсии случайной ошибки модели, или условной по факторам дисперсии зависимой переменной) в дисперсии зависимой переменной. Его рассматривают как универсальную меру зависимости одной случайной величины от множества других. В частном случае линейной зависимости является квадратом так называемого множественного коэффициента корреляции между зависимой переменной и объясняющими переменными. В частности, для модели парной линейной регрессии коэффициент детерминации равен квадрату обычного коэффициента корреляции между y и x.

6. Перечислите этапы построения эконометрической модели.

Весь процесс эконометрического моделирования можно разбить на шесть основных этапов.

1-й этап (постановочный) - определение конечных целей моделирова­ния, набора участвующих в модели факторов и показателей, их роли;

2-й этап (априорный) - предмодельный анализ экономической сущности изучаемого явления, формирование и формализация априорной информации и исходных допущений,

3-й этап (параметризация) - собственно моделирование, т.е. выбор общего вида модели, в том числе состава и формы входящих в неё связей между переменными;

4-й этап (информационный) - сбор необходимой статистической информации, т.е. регистрация значений участвующих в модели факторов и показате­лей;

5-й этап (идентификация модели) - статистический анализ модели и в первую очередь статистическое оценивание неизвестных параметров модели Непосредственно связан с проблемой идентифицируемости модели, то есть ответа на вопрос «Возможно ли в принципе однозначно восстановить значения неизвестных параметров модели по имеющимся исходным данным в соответст-вии с решением, принятым на этапе параметризации?». После положительного ответа на этот вопрос необходимо решить проблему идентификации модели то есть предложить и реализовать математически корректную процедуру оценива­ния неизвестных параметров модели по имеющимся исходным данным;

6-й этап (верификация модели) — сопоставление реальных и модельных данных, проверка адекватности модели, оценка точности модельных данных.

7. Что такое ковариация?

Ковариация (от англ. covariation - "совместная вариация") - мера линейной зависимости двух величин. она показывает, есть ли линейная взаимосвязь между двумя случайными величинами, и может рассматриваться как "двумерная дисперсия".

Знак ковариации указывает на вид линейной связи между рассматриваемыми величинами: если она > 0 - это означает прямую связь (при росте одной величины растет и другая), ковариация < 0 указывает на обратную связь. При ковариации = 0 линейная связь между переменными отсутствует.

8. Что такое мода?

Мода Мо наиболее часто встречающееся в данной совокупности значение признака, т. е. это варианта с наибольшей частотой. Мо не отражает степени модальности, т. е. не несет в себе информацию о том, насколько распространено данное значение признака в изучаемой совокупности.

9. Раскройте понятие медианы.

Медиа́на (50-й перцентиль, квантиль 0,5) — возможное значение признака, которое делит ранжированную совокупность (вариационный ряд выборки) на две равные части: 50 % «нижних» единиц ряда данных будут иметь значение признака не больше, чем медиана, а «верхние» 50 % — значения признака не меньше, чем медиана.

10. Что такое дисперсия?

Диспе́рсия случа́йной величины́ — мера разброса данной случайной величины, то есть её отклонения от математического ожидания. Квадратный корень из дисперсии, равный , называется среднеквадрати́чным отклоне́нием, станда́ртным отклоне́нием или стандартным разбросом.

Стандартное отклонение измеряется в тех же единицах, что и сама случайная величина, а дисперсия измеряется в квадратах этой единицы измерения. Формула для расчета дисперсии выглядит так:

 

где

D – дисперсия,

x – анализируемый показатель, с черточкой сверху – среднее значение показателя,

n – количество значений в анализируемой совокупности данных.

11. Как оценивают корреляционную связь?

С помощью коэфф. корреляции

Сила связи	Направление связи
	прямая (+)	обратная (-)
Сильная	от + 1 до +0,7	от - 1 до - 0,7
Средняя	от + 0,699 до + 0,3	от - 0,699 до - 0,3
Слабая	от + 0,299 до 0	от - 0,299 до 0

Шкала Чеддока

R	Интерпретация
0.1 ÷ 0.3 0.3 ÷ 0.5 0.5 ÷ 0.7 0.7 ÷ 0.9 0.9 ÷ 1.0	Слабая Умеренная Заметная Высокая Весьма высокая

12. Какие гипотезы проверяются с помощью критерия согласия Пирсона?

Критерий согласия Пирсона (χ²) применяют для проверки гипотезы о соответствии эмпирического распределения предполагаемому теоретическому распределению F(x) при большом объеме выборки (n ≥ 100). Критерий применим для любых видов функции F(x), даже при неизвестных значениях их параметров, что обычно имеет место при анализе результатов механических испытаний. В этом заключается его универсальность.

13. Какие гипотезы проверяются с помощью критерия согласия Колмогорова – Смирнова?

Критерий согласия Колмогорова - Смирнова позволяет проверить гипотезу о согласии при небольшом объеме выборки, когда Fmod известна полностью, т. е. известны и параметры модели [1,6, 12, 15]. 

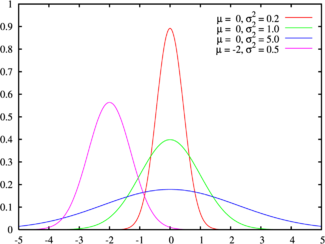
14. Дайте краткую характеристику понятию «нормальное распределение», изобразите график.

Нормальное распределение,^[1][2] также называемое распределением Гаусса — распределение вероятностей, которое в одномерном случае задается функцией плотности вероятности, совпадающей с функцией Гаусса:

где параметр μ — математическое ожидание, медиана и мода распределения, а параметр σ — стандартное отклонение (σ² — дисперсия) распределения.

Таким образом, одномерное нормальное распределение является двухпараметрическим семейством распределений. Многомерный случай описан в многомерном нормальном распределении.

Стандартным нормальным распределением называется нормальное распределение с математическим ожиданием μ = 0 и стандартным отклонением σ = 1.

15. Что такое эксцесс?

Коэффицие́нт эксце́сса (коэффициент островершинности) в теории вероятностей — мера остроты пика распределения случайной величины.

16. Что такое асимметрия

Асимметрия представляет  собой числовое отображение степени отклонения графика распределения показателей от симметричного графика распределения.Показатель асимметрии вычисляется по формуле:

Асимметрия симметричного распределения равно 0

Если асимметрия больше 0, то чаще в распределении встречаются значения меньше среднего. Такая асимметрия называется положительной или левосторонней.

Если асимметрия меньше 0, то в распределении чаще встречаются значения больше среднего. Такая асимметрия называется отрицательной или правосторонней.

17. Дайте определение регрессии: парная и множественная.

Регрессия - зависимость среднего значения какой-либо величины от некоторой другой величины или от нескольких величин

Парная регрессия - это уравнение связи двух переменных у и х, где у - зависимая переменная. Множетсвенная – больше 2х

18. Как оценить значимость коэффициентов регрессии?

Значимость коэфициентов регрессии можно определить с помощью:

• критического значения t-статистик Стьюдента для каждого коэффициента регрессии (t-Statistic),

• p-значения (фактические вероятности принятия нулевой гипотезы) для каждого коэффициента регрессии (Prob).

19. Что такое t – статистика?

T-статистика (t-критерий Стьюдента) используется для проверки значимости каждого фактора регрессионной модели.

20. Что такое р – значение?

P-значение (англ. P-value) — величина, используемая при тестировании статистических гипотез. Фактически это вероятность ошибки при отклонении нулевой гипотезы (ошибки первого рода). Проверка гипотез с помощью P-значения является альтернативой классической процедуре проверки через критическое значение распределения. Обычно P-значение равно вероятности того, что случайная величина с данным распределением (распределением тестовой статистики при нулевой гипотезе) примет значение, не меньшее, чем фактическое значение тестовой статистики.

21. Какие методы построения линейной регрессии Вы знаете?

1.парной линейной регрессии-методом наименьших квадратов

2.линейной- MS EXCEL

3. и наверно в SPSS

22. Что показывает коэффициент разбухания дисперсии?

23. Что такое мультиколлинеарность?

Мультиколлинеарность (multicollinearity) — в эконометрике (регрессионный анализ) — наличие линейной зависимости между независимыми переменными (факторами) регрессионной модели. При этом различают полную коллинеарность, которая означает наличие функциональной (тождественной) линейной зависимости и частичную или просто мультиколлинеарность — наличие сильной корреляции между факторами.

Полная коллинеарность приводит к неопределенности параметров в линейной регрессиионной модели независимо от методов оценки.

24. Объясните понятие «фиктивные» переменные.

Фиктивная переменная (англ. dummy variable) — качественная переменная, принимающая значения 0 и 1, включаемая в эконометрическую модель для учёта влияния качественных признаков и событий на объясняемую переменную. При этом фиктивные переменные позволяют учесть влияние не только качественных признаков принимающих два, но и несколько возможных значения. В этом случае добавляются несколько фиктивных переменных. Фиктивная переменная может быть также индикатором принадлежности наблюдения к некоторой подвыборке. Последнее можно использовать для обнаружения структурных изменений.

25. Дайте определение понятию «гетероскедастичность»?

ГЕТЕРОСКЕДАСТИЧНОСТЬ [heteroscedasticity] (неоднородность) — понятие математической статистики и эконометрии; означает ситуацию, когда дисперсия ошибки в уравнении регрессии изменяется от наблюдения к наблюдению

26. Какие способы позволяют выявить гетероскедастичность?

27. Поясните смысл метода наименьших квадратов.

Суть метода наименьших квадратов (МНК). Задача заключается в нахождении коэффициентов линейной зависимости, при которых функция двух переменных а и b принимает наименьшее значение. То есть, при данных а и b сумма квадратов отклонений экспериментальных данных от найденной прямой будет наименьшей. В этом вся суть метода наименьших квадратов.

28. В чем заключается смысл теста Глейзера?

Тест Глейзера — статистический тест, позволяющий оценить наличие (отсутствие) гетероскедастичности (определенного вида) случайных ошибок регрессионной (эконометрической) модели.

Тест основан на следующей модели возможной зависимости стандартного отклонения случайной ошибки модели от некоторого фактора :

Нулевая гипотеза заключается в равенстве коэффициента нулю (отсутствие гетероскедастичности данного вида). Если в тесте отвергается нулевая гипотеза, то гетероскедастичность данного вида признается статистически значимой. Если нулевая гипотеза не отвергается, то скорее всего гетероскедастичности данного вида нет в модели (однако, это не исключает возможность гетероскедастичности другого вида).

29. Какой метод применяется в целях устранения гетероскедастичности?

Для устранения гетероскедастичности или смягчения этой проблемы можно использовать так называемый взвешенный МНК (ВМНК).

30. Как оценить эффективность модели линейной регрессии?

Модель линейной регрессии (линейное уравнение) является наиболее распространенным (и простым) видом зависимости между экономическими переменными. Определить тип уравнения можно, исследуя зависимость графически. Сущность МНК заключается в нахождении параметров модели (а0, а1), при которых минимизируется сумма квадратов отклонений эмпирических (фактических) значений результативного признака от теоретических, полученных по выбранному уравнению регрессии: . Проводят дифференцирование S по коэффицентам и приравнивают уравнения к 0. Из системы уравнений, получаем:  Здесь Параметр а1 называется коэффициентом регрессии. Его величина показывает среднее изменение результата с изменением фактора на единицу. После того как получено уравнение множественной регрессии, необходимо измерить тесноту связи между результативным признаком и факторными признаками. Для измерения степени совокупного влияния отобранных факторов на результативный признак рассчитывают совокупный коэффициент детерминации R2 и совокупный коэффициент множественной корреляции R - общие показатели тесноты связи многих признаков. Проверка адекватности моделей, построенных на основе уравнений регрессии, начинается с проверки значимости каждого коэффициента регрессии. Значимость коэффициента регрессии осуществляется с помощью t-критерия Стьюдента (отношение коэффициента регрессии к его средней ошибке): . Коэффициент регрессии считается статистически значимым, если  превышает tтабл  - табличное (теоретическое) значение t-критерия Стьюдента. Проверка адекватности всей модели осуществляется с помощью F-критерия и величины средней ошибки аппроксимации . Значение средней ошибки аппроксимации, определяемой по формуле не должно превышать 12 - 15 %. Расчетное значение F-критерия определяется по формуле и сравнивается с табличным: , где  - коэффициент множественной детерминации. Если Fрасч  Fтабл, связь признается существенной

31. Дать полное определение понятию «временной ряд»?

Временно́й ряд (или ряд динамики) — собранный в разные моменты времени статистический материал о значении каких-либо параметров (в простейшем случае одного) исследуемого процесса. Каждая единица статистического материала называется измерением или отсчётом, также допустимо называть его уровнем на указанный с ним момент времени. Во временном ряде для каждого отсчёта должно быть указано время измерения или номер измерения по порядку. Временной ряд существенно отличается от простой выборки данных, так как при анализе учитывается взаимосвязь измерений со временем, а не только статистическое разнообразие и статистические характеристики выборки^[1].

32. Что показывает линия тренда?

Линию тренда или линейную фильтрацию можно добавить к любому ряду данных на диаграмме без накопления, плоской диаграмме, диаграмме с областями, линейчатой диаграмме, гистограмме, графике, биржевой, точечной или пузырьковой диаграмме. Линия тренда всегда связана с рядом данных, но не представляет данные этого ряда. Она предназначена для отображения тенденций в существующих данных или прогнозов будущих данных.

33. Раскройте понятие временной лаг.

В реальной экономике и в экономических моделях задержка, в связи с возникновением определенных событий после совершения действий, которые, как полагают, их вызвали. Временные лаги возникают несколькими путями. Во-первых, существует лаг из-за сбора, обработки и распространения экономической информации. Во-вторых, даже когда информация доступна, принимающие экономические решения лица зачастую откладывают действия до получения большего объема информации с целью определения, являются ли данные изменения временными или постоянными, или в результате споров о том, каким должен быть ответ. В-третьих, даже когда решение принято, приведение его в действие занимает какое-то время: в некоторых случаях, например при открытии нового завода в ответ на увеличение спроса, задержка может быть значительной. Поэтому временные лаги распространены довольно широко.

34. Что такое автокорреляция.

Автокорреляция — статистическая взаимосвязь между последовательностями величин одного ряда, взятыми со сдвигом, например, для случайного процесса — со сдвигом по времени.

А- это измерение зависимости между значением какой-либо величины из временного ряда и ее предыдущими или последующими значениями. Автокорреляцией первого порядка называют зависимость между значением данной величины и ее непосредственно предшествующим или следующим значением

35. Что показывает статистика Дарбина – Уотсона? Изобразите шкалу оценки автокорреляции.

Используется для определения наличия/отсутствия автокорреляции между случайными членами   которая выражается коэффициентом корреляции  .

n

k = 1

k = 2

k = 3

k = 4

k = 5

dL

dU

dL

dU

dL

dU

dL

dU

dL

dU

36. В чем смысл преобразования Бокса-Дженкинса?

Методика предусматривает такие последовательные процедуры:

1) идентификация модели временного ряда;

2) оценивание параметров модели;

3) диагностика построенной модели;

4) использование модели для прогнозирования будущих значений временного ряда.

Главная идея применения метода состоит в предположении, что данные имеют некоторое вероятностное распределение и исчисляются вероятность нужного события. Это в общем случае зависит от некоторых неизвестных параметров.

37. В чем заключается смысл процесса «белый шум»?

Белым шумом называется случайная последовательность значений y1, y2,…,yN, если её математическое ожидание равно нулю, т.е. E(Yt)=0, где

её элементы являются некоррелированными (независимыми друг от друга) одинаково распределёнными величинами, и дисперсия является постоянной величиной D(Yt)=G2=const.

Белый шум – это теоретический процесс, который реально не существует, однако он представляет собой очень важную математическую модель, которая используется при решении множества практических задач.

38. Каковы предпосылки «классического» МНК?