8. Математическое ожидание (мо), его свойства. Вычисление мо экспоненциального распределения.

Определение.

Математическим ожиданием СВ называется число ,которое определяется для дискретных СВ как а для непрерывных как

В этом определении символ МХ (в англоязычной литературе обозначается через  ) означает операцию (оператор) вычисления математического ожидания. Из определения следует, что МО является средним по вероятности значением СВ. Поэтому вместо МО часто используется термин среднее значение или просто среднее СВ.

Свойства МО.

1°. Математическое ожидание постоянной С равно этой постоянной.     Доказательство. Постоянную C можно рассматривать как случайную величину  , которая может принимать только одно значение C c вероятностью равной единице. Поэтому       2°. Постоянный множитель можно выносить за знак математического ожидания, т.е.

   Доказательство. Используя соотношение (39), имеем

   3°. Математическое ожидание суммы нескольких случайных величин равно сумме математических ожиданий этих величин:

(41)

   4°. Математическое ожидание произведения двух независимых случайных величин равно произведению математических ожиданий этих величин :

Вычисление МО экспоненциального распределения.

9. Дисперсия, ее свойства. Вычисление дисперсии экспоненциального распределения.

Дисперсией   случайной величины   называется математическое ожидание квадрата отклонения случайной величины от ее математичекого ожидания *:

Пусть   - дискретная случайная величина, принимающая значения x₁, x₂, ..., x_n соответственно с вероятностями p₁, p₂, ..., p_n.

Дисперсия характеризует степень разброса значений случайной величины относительно ее математического ожидания, т.е. ширину диапазона значений.

Свойства дисперсии

• Дисперсия постоянной величины с равна нулю.

Доказательство: по определению дисперсии

• При прибавлении к случайной величине Х неслучайной величины с ее дисперсия не меняется. D[X+c] = D[X].

Доказательство: по определению дисперсии

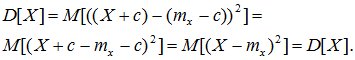
• При умножении случайной величины Х на неслучайную величину с ее дисперсия умножается на с².

Доказательство: по определению дисперсии

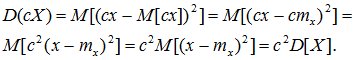
• Правило 3s. Для большинства значений случайной величины абсолютная величина ее отклонения от математического ожидания не превосходит утроенного среднего квадратического отклонения, или, другими словами, практически все значения СВ находятся в интервале: [ m - 3s; m + 3s; ]

Вычисление дисперсии экспоненциального распределения.

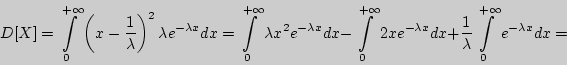
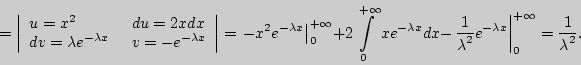
10. Ковариация и корреляция. Свойства

При изучении многомерных СВ (случайная величина) важное значение имеют их взаимозависимости и зависимости. Рассмотрим некоторые характеристики зависимости и связи СВ. Остановимся на характеристиках зависимости и взаимозависимости между двумя СВ. (В случае многомерной СВ можно изучать попарную зависимости ее компонент). Взаимозависимость между СВ может быть измерена с помощью коэффициентов ковариации и корреляции.

Коэффициентом ковариации СВ Х и Y называется число, которое вычисляется для дискретных СВ по формуле

Kxy=cov(X,Y)=

А для непрерывных - по формуле

Kxy=cov(X,Y)=

Здесь Pij=P(X=xi, Y=yj) – распределение СВ (X,Y) в дискретном случае, а p(x,y) – ПР СВ (X,Y ) – в непрерывном.

Более удобным для характеризации зависимости (как станет видно из следующей ниже теоремы) является нормированный аналог коэффициента ковариации – коэффициент корреляции, который определяется как

ρXY =

Из определения вытекают следующие свойства коэффициента корреляции:

Теорема 3 (Свойства корреляции). Коэффициент корреляции обладает следующими свойствами:

1) ρ(X,Y ) = ρ(Y ,X);

2) ρ(X,Y )| ≤ 1, или −1 ≤ ρ(X,Y ) ≤ 1;

3) Для независимых СВ X и Y ρ(X,Y ) = 0; 4) ρ(X,Y ) = 1 тогда и только тогда, когда Y = aX + b.

Доказательство опускаем.

Приведенные свойства коэффициента корреляции позволяют рассматривать его как меру взаимозависимости СВ. Действительно, свойство 3) показывает, что коэффициент корреляции независимых СВ минимален по абсолютному значению и равен нулю, а из свойства 4) следует, что он максимален по абсолютному значению и равен единице тогда и только тогда, когда между СВ существует сильная линейная зависимость.

11. выборка, вариационный ряд, выборочная медиана.

Набор всех возможных значений наблюдаемой СВ в статистике принято называть генеральной совокупностью. Материалом для статистического анализа являются наблюдения 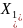, Х₂,..., Х_п над элементами генеральной совокупности. Результат х = ( ,х₂,..., х_п) п наблюдений над элементами генеральной совокупности называют выборкой объема п из данной генеральной совокупности, или просто выборкой.

Пусть имеется выборка х = (х₁,х₂,... ,х_п) из генеральной

совокупности по одному числовому признаку. Упорядоченная в порядке возрастания элементов выборка

x(1), x(2), · · · , x(n) С x(i) x(i+1)

называется вариационным рядом, а ее элементы вариантами, или порядковыми статистиками. При этом минимальный и максимальный члены выборки совпадают соответственно с первым и последним (крайними) членами вариационного ряда: = min_i x_i = x(₁), 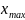= max_i x_i = x(_n).

Выборочной медианой называется значение выборки, делящее ее на две равные части.

По вариационному ряду легко построить выборочные медиану и квантили .

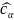12. Эмпирическая функция распределения (ЭФР). Связь ФР и ЭФР

Эмпирической или выборочной ф-ей распределения (ЭФР) случайно величины Х называется выборочная вероятность того, что Х ≤ х, определённая для всех допустимых значений переменной х.

ЭФР можно определить по формуле:

ЭФР имеет «ступенчатый» вид, как и ФР дискретной СВ. Таким образом, непрерывная случайная величина приближённо заменяется дискретной.