1.Функция распределения и её свойства.

Функцией распределения случайной величины называется функция

Из определения следуют свойства ФР, которые содержатся в следующей теореме.

Теорема: Всякая функция распределения обладает следующими свойствами:

1).0≤F(x)≤1-ограниченность

2).F(x)≤F(y) при x≤y-монотонность

3).

4).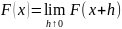 -непрерывность справа

Функция распределения дискретной случайной величины

Если x - дискретная случайная величина, принимающая значения x₁ < x₂ < … < x_i < … с вероятностями p₁ < p₂ < … < p_i < …, то таблица вида

x1	x2	…	xi	…
p1	p2	…	pi	…

называется распределением дискретной случайной величины.

Функция распределения случайной величины, с таким распределением, имеет вид

Функция распределения и плотность вероятности непрерывной случайной величины

Если функция распределения F_x (x) непрерывна, то случайная величина x называется непрерывной случайной величиной.

Если функция распределения непрерывной случайной величины дифференцируема, то более наглядное представление о случайной величине дает плотность вероятности случайной величины p_x (x), которая связана с функцией распределения F_x (x) формулами

 и  .

Отсюда, в частности, следует, что для любой случайной величины  .

2. Схема Бернулли: биномиальное и геометрическое распределение

Схема Бернулли-модель с независимым повторением экспериментов с 2мя исходами.

Если в таком эксперименте наблюдаются числовые исходы, соответствующее распределение- распределение Бернулли P{X=1}=p, P{X=0}=1-p=q

Биномиальное распределение (Распределение Sn)- последовательность из n независимых испытаний Бернулли, СВ принимают значение 1- успех, 0-неудача. Sn- число «успешных» исходов из n испытаний (Sn = 0, 1,..n).

Геометрическое распределение (распределение Т - число испытаний до первого неуспешного исхода)-

3. Плотность распределения (пр), ее свойства

Пусть имеется непрерывная случайная величина   с функцией распределения   , которую мы предположим непрерывной и дифференцируемой.

.           

Функция   - производная функции распределения – характеризует как бы плотность, с которой распределяются значения случайной величины в данной точке. Эта функция называется плотностью распределения (иначе – «плотность вероятности») непрерывной случайной величины  .

Основные свойства плотности распределения.

1.  Плотность распределения есть неотрицательная функция:

.

Это свойство непосредственно вытекает  из того, что функция распределения   есть неубывающая функция.

2. Интеграл в бесконечных пределах от плотности распределения равен единице:

.

Это следует из того, что  .

Геометрически основные свойства плотности распределения означают, что:

1) вся кривая распределения лежит не ниже оси абсцисс;

2) полная площадь, ограниченная кривой распределения и осью абсцисс, равна единице.