8.5. Анализ устойчивости по лчх

Оценку устойчивости по критерию Найквиста удобнее производить по ЛЧХ разомкнутой САУ. Очевидно, что каждой точке АФЧХ будут соответствовать определенные точки ЛАЧХ и ЛФЧХ.

Пусть известны частотные характеристики двух разомкнутых САУ (1 и 2), отличающихся друг от друга только коэффициентом передачи K₁ < K₂. Пусть первая САУ устойчива в замкнутом состоянии, вторая нет (рис.91).

 

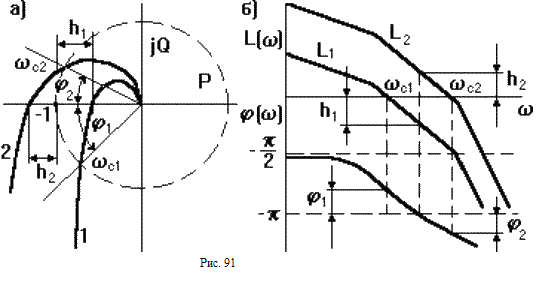
 Если W₁(p) - передаточная функция первой САУ, то передаточная функция второй САУ W₂(p) = K W₁(p), где K = K₂/K₁. Вторую САУ можно представить последовательной цепочкой из двух звеньев с передаточными функциями K (безынерционное звено) и W₁(p), поэтому результирующие ЛЧХ строятся как сумма ЛЧХ каждого из звеньев.

Поэтому ЛАЧХ второй САУ: L₂( ) = 20lgK + L₁( ),

а ЛФЧХ: ₂( ) = ₁( ).

Пересечениям АФЧХ вещественной оси соответствует значение фазы = - . Это соответствует точке пересечения ЛФЧХ = - линии координатной сетки. При этом, как видно на АФЧХ, амплитуды A₁( ) < 1, A₂( ) > 1, что соответствует на САЧХ значениям L₁( ) = 20lgA₁( ) < 0 и L₂( ) > 0.

Сравнивая АФЧХ и ЛФЧХ можно заключить, что система в замкнутом состоянии будет устойчива, если значению ЛФЧХ = - будут соответствовать отрицательные значения ЛАЧХ и наоборот. Запасам устойчивости по модулю h₁ и h₂, определенным по АФЧХ соответствуют расстояния от оси абсцисс до ЛАЧХ в точках, где = - , но в логарифмическом масштабе.

Особыми точками являются точки пересечения АФЧХ с единичной окружностью. Частоты _c1 и _c2, при которых это происходит называют частотами среза.

В точках пересечения A( ) = 1 = > L( ) = 0 - ЛАЧХ пересекает горизонтальную ось. Если при частоте среза фаза АФЧХ _c1 > - (рис.91 а кривая 1), то замкнутая САУ устойчива. На рис.79б это выглядит так, что пересечению ЛАЧХ горизонтальной оси соответствует точка ЛФЧХ, расположенная выше линии = - . И наоборот для неустойчивой замкнутой САУ (рис.91 а кривая 2) _c2 < - , поэтому при = _c2 ЛФЧХ проходит ниже линии = - . Угол ₁ = _c1-(- ) является запасом устойчивости по фазе. Этот угол соответствует расстоянию от линии = - до ЛФЧХ.

Исходя из сказанного, критерий устойчивости Найквиста по логарифмическим ЧХ, в случаях, когда АФЧХ только один раз пересекает отрезок вещественной оси [- ;-1], можно сформулировать так: для того, чтобы замкнутая САУ была устойчива необходимо и достаточно, чтобы частота, при которой ЛФЧХ пересекает линию = - , была больше частоты среза.

 

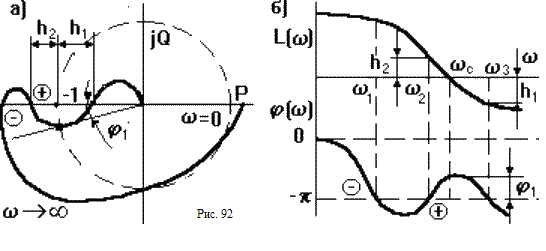
 Если АФЧХ разомкнутой САУ имеет сложный вид (рис.80), то ЛФЧХ может несколько раз пересекать линию = - . В этом случае применение критерия Найквиста несколько усложняется. Однако во многих случаях данной формулировки критерия Найквиста оказывается достаточно.

8.6. Теоретическое обоснование метода d-разбиений

 Изменение параметров САУ, например, с целью оптимизации, приведет к изменению коэффициентов уравнения динамики. Останется ли при этом САУ устойчивой - неизвестно. Критерии устойчивости об этом ничего не говорят. Рассмотрим метод определения границ допустимых изменений параметров, при которых САУ не теряет устойчивости.

Приведем характеристическое уравнение замкнутой САУ к виду:

  D(p) = pⁿ + c¹ p^{n -1} + c² p^n-2 + ... + cⁿ = 0,

где c⁰ = a⁰ /a⁰ = 1, c¹ = a¹ /a⁰ и т.д. При некоторых конкретных значениях c¹ ,c² ,...,cⁿ уравнение имеет единственное решение, то есть единственный набор корней (p¹ , p² ,...,p_n ). По их расположению на комплексной плоскости можно судить об устойчивости САУ при заданных параметрах. Если изменить какой-либо параметр САУ, например коэффициента передачи, то изменятся и коэффициенты характеристического уравнения D(p) = 0 и станут равными c^н1 ,c^н2 ,...,c^нn . Уравнение примет вид:

D _н(p) = pⁿ + c^н1 p^{n -1} + c^н2 p^{n -2} + ... + c^нn = 0.

Это уже другое уравнение и оно также имеет единственное решение (p^н1 ,p^н2 ,...,p^нn ), отличающееся от (p¹ ,p² ,...,pⁿ ). Если плавно менять значение параметра САУ, то коэффициенты уравнения тоже будут плавно изменяться, а его корни будут перемещаться по комплексной плоскости (рис.93).

Каждый уникальный набору коэффициентов c¹ ,c² ,...,cⁿ  можно изобразить точкой в пространстве коэффициентов, по осям которого откладываются значения коэффициентов c¹ ,c² ,...,cⁿ . Так уравнению третьей степени соответствует трехмерное пространство коэффициентов (рис.94). Пусть точка N с координатами (c_N1 ,c_N2,c_N3) соответствует уравнению, имеющему решение (p_N1,p_N2,p_N3), точка M с координатами (c_M1 ,c_M2 ,c_M3) соответствует уравнению, имеющему решение (p_M1 ,p_M2 ,p_M3). При изменении какого-либо параметра САУ коэффициенты характеристического уравнения будут изменяться, при этом точка в пространстве коэффициентов, соответствующая данному уравнению будет перемещаться по некоторой траектории, например из положения N в положение M. Этому перемещению будет соответствовать и перемещение корней (p_N1,p_N2,p_N3) на комплексной плоскости в положение (p_M1 ,p_M2 ,p_M3) (аналогично рис.93).

П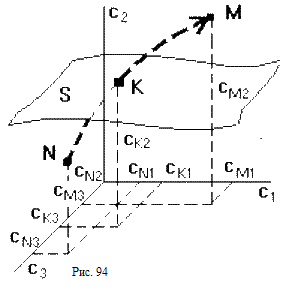 ри этом движении некоторые корни будут переходить через мнимую ось комплексной плоскости из левой полуплоскости в правую и наоборот. В момент перехода такой k-й корень примет значение p_K = j _K, а коэффициенты уравнения будут иметь определенные значения c_K1,c_K2,c_K3, определяющие в пространстве коэффициентов точку K. Подставим корень p_K в характеристическое уравнение, получим тождество:

D(p_K ) = (j _K)³ + cK1(j _K)² + c_K2 (jK ) + c_K3 = 0

Меняя w от - до + , и находя при каждой частоте все возможные сочетания коэффициентов c¹ ,c² ,...,cⁿ , удовлетворяющих уравнению

D(j ) = (j )ⁿ + c¹ (j )^n-1 + c² (j )^n-2 + ... + cⁿ = 0,

можно построить в n-мерном пространстве коэффициентов сложную поверхность S, разделяющую его на области, называемое D-областями. Полученное уравнение называется уравнением границы D-разбиения.

Переход из одной D-области в другую через поверхность S соответствует переходу одного или нескольких корней через мнимую ось в плоскости корней. То есть каждая точка внутри определенной D-области соответствует уравнению с определенным количеством левых и правых корней. Поэтому области обозначают D(m) по числу m правых корней.

Достаточно взять любую точку в пространстве коэффициентов и найти для нее число правых корней. Затем, двигаясь по пространству коэффициентов через границу S, можно выявить обозначения всех других областей. Особый интерес представляет область D(0), которой соответствуют уравнения с полным отсутствием правых корней, называемая областью устойчивости. Описанный метод определения областей устойчивости называется методом D-разбиений.

Не обязательно строить сложную n-мерную картину D-разбиения, можно изменять значения, например, только двух коэффициентов, оставляя другие коэффициенты постоянными. Границу D-разбиения S можно строить не только также и в пространстве конкретных параметров системы, от которых зависят данные коэффициенты.

D-разбиение по одному параметру

Пусть необходимо выявить влияние на устойчивость САУ, например, коэффициента усиления K. Приведем характеристическое уравнение к виду D(p) = S(p) + K N(p), выделив члены, не зависящие от K в полином S(p), а в остальных членах, линейно зависящих от K, вынесем его за скобки. Граница D-разбиения задается уравнением

 D(j ) = S(j ) + K N(j ) = 0,  => K = -S(j )/N(j ) = X( ) + jY( ).

 Изменяя w от - до + , будем вычислять X( ) и Y( ) и по ним строить точки границы D-разбиения. Пространство коэффициентов представляется системой координат X-Y (рис.83а). Обычно строят только половину кривой ( = [0, + ), другую половину достраивают симметрично относительно вещественной оси.

Е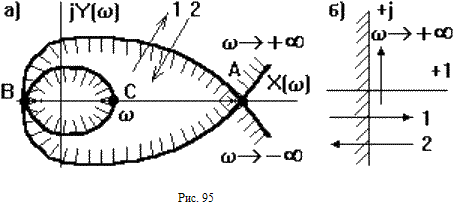 сли в плоскости корней двигаться вдоль мнимой оси от - до + и штриховать ее слева (рис.95 б), то это будет соответствовать движению вдоль линии D-разбиения при изменении w от - до + и штриховке ее также слева. Переходу корня в плоскости корней из штрихованной полуплоскости в нештрихованную вдоль стрелки 1 соответствует аналогичный переход через границу D-разбиения вдоль стрелки 1, и наоборот. Если пересекается область с двойной штриховкой (точки A, В, C), то в плоскости корней мнимую ось пересекает пара комплексно сопряженных корней.

Если известно количество правых корней, соответствующее хотя бы одной D-области, то двигаясь от нее через границы с учетом штриховок, можно обозначить все остальные области. Область с наибольшим количеством штриховок является претендентом на область устойчивости. Нужно взять любую точку из этой области и при соответствующем значении K проверить систему на устойчивость любым методом.

Есть одна особенность. Так как K - вещественное число, то Y( ) = 0, поэтому нас интересует не вся область устойчивости, а лишь отрезок вещественной оси в этой области, то есть K = X( ).