Формулировка[править | править исходный текст]

Теорема. Если вероятность   наступления события   в каждом испытании постоянна, то вероятность   того, что событие   наступит   раз в   независимых испытаниях, равна:  , где  .

Доказательство

Пусть проводится   независимых испытаний, причём известно, что в результате каждого испытания событие   наступает с вероятностью   и, следовательно, не наступает с вероятностью  . Пусть, так же, в ходе испытаний вероятности   и   остаются неизменными. Какова вероятность того, что в результате   независимых испытаний, событие   наступит ровно   раз?

Оказывается можно точно подсчитать число "удачных" комбинаций исходов испытаний, для которых событие   наступает   раз в   независимых испытаниях, - в точности это количество сочетаний из   по  :

.

В то же время, так как все испытания независимы и их исходы несовместимы (событие   либо наступает, либо нет), то вероятность получения "удачной" комбинации в точности равна:  .

Окончательно, для того чтобы найти вероятность того, что в   независимых испытаниях событие   наступит ровно   раз, нужно сложить вероятности получения всех "удачных" комбинаций. Вероятности получения всех "удачных" комбинаций одинаковы и равны  , количество "удачных" комбинаций равно  , поэтому окончательно получаем:

.

Последнее выражение есть не что иное, как Формула Бернулли. Полезно так же заметить, что в силу полноты группы событий, будет справедливо:

.

15.

Распределение Пуассона — вероятностное распределение дискретного типа, моделирует случайную величину, представляющую собой числособытий, произошедших за фиксированное время, при условии, что данные события происходят с некоторой фиксированной средней интенсивностью инезависимо друг от друга.

Распределение Пуассона играет ключевую роль в теории массового обслуживания.

Определение[править | править исходный текст]

Выберем фиксированное число   и определим дискретное распределение, задаваемое следующей функцией вероятности:

,

где

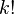•  обозначает факториал числа  ,

•  — основание натурального логарифма.

Тот факт, что случайная величина   имеет распределение Пуассона с параметром  , записывается:  .

Моменты[править | править исходный текст]

Производящая функция моментов распределения Пуассона имеет вид:

,

откуда

,

.

Для факториальных моментов распределения справедлива общая формула:

,

где 

А так как моменты и факториальные моменты линейным образом связаны, то часто для пуассоновского распределения исследуются именно факториальные моменты, из которых при необходимости можно вывести и обычные моменты.

Свойства распределения Пуассона[править | править исходный текст]

Сумма независимых пуассоновских случайных величин также имеет распределение Пуассона. Пусть  . Тогда

.

Пусть  , и  . Тогда условное распределение   при условии, что  , биномиально. Более точно:

.

ПУАССОНА ФОРМУЛА

- 1) То же, что Пуассона интеграл.2) Формула, дающая интегральное представление решения задачи Коши для волнового уравнения в пространстве  :

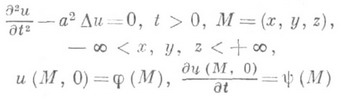
и имеющая вид 

 (1) где 

- среднее значение функции j на сфере S_at в пространстве ( х, у, z) радиуса at с центром в точке М, dW- элемент площади единичной сферы. В случае неоднородного волнового уравнения в формуле (1) добавляется третье слагаемое (см. [2]).

Из формулы (1) спуска методом получаются формулы решения задачи Копти для случая двух (Пуассона формула) и одного (Д ¹ Аламбера формула) пространственного переменного (см. [2]). См. также Кирхгофа формула.

3) Иногда П. ф. наз. интегральное представление решения задачи Коши для уравнения теплопроводности в пространстве  :

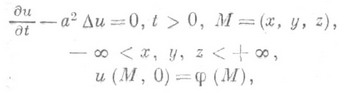
имеющее вид 

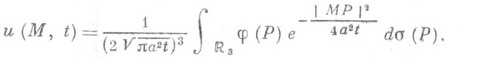 (2)

Формула (2) непосредственно обобщается на любое число пространственных переменных