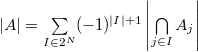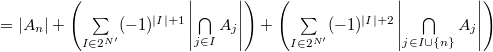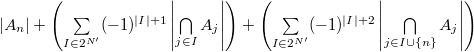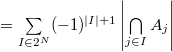Обратный ход метода Гаусса: преобразование полученной ступенчатой матрицы к матрице, в первых n столбцах которой содержится единичная матрица  ,  последний, (n+1)-й, столбец этой матрицы содержит решение системы.

.

37.решение слау с помощью обратной матрицы

Решение системы с помощью обратной матрицы

Метод обратной матрицы – это, по существу, частный случай матричного уравнения (см. Пример №3 указанного урока).

Для изучения данного параграфа необходимо уметь раскрывать определители, находить обратную матрицу и выполнять матричное умножение. Соответствующие ссылки будут даны по ходу объяснений.

Пример 11

Решить систему с матричным методом  

Решение: Запишем систему в матричной форме:  , где  

Пожалуйста, посмотрите на систему уравнений и на матрицы. По какому принципу записываем элементы в матрицы, думаю, всем понятно. Единственный комментарий: если бы в уравнениях отсутствовали некоторые переменные, то на соответствующих местах в матрице   нужно было бы поставить нули.

Решение системы найдем по формуле  (её подробный вывод можно посмотреть в статье Матричные уравнения).

Согласно формуле нам нужно найти обратную матрицу   и выполнить матричное умножение  . Алгоритм нахождения обратной матрицы подробно разобран на уроке Как найти обратную матрицу?

Обратную матрицу найдем по формуле: , где   – транспонированная матрица алгебраических дополнений соответствующих элементов матрицы  .

Сначала разбираемся с определителем:

Здесь определитель раскрыт по первой строке.

Внимание! Если  , то обратной матрицы не существует, и решить систему матричным методом невозможно. В этом случае система решается методом исключение неизвестных (методом Гаусса).

Теперь нужно вычислить 9 миноров и записать их в матрицу миноров 

Справка: Полезно знать смысл двойных подстрочных индексов в линейной алгебре. Первая цифра – это номер строки, в которой находится данный элемент. Вторая цифра – это номер столбца, в котором находится данный элемент: То есть, двойной подстрочный индекс указывает, что элемент   находится в первой строке, третьем столбце, а, например, элемент   находится в 3 строке, 2 столбце

В ходе решения расчет миноров лучше расписать подробно, хотя, при определенном опыте их можно приноровиться считать с ошибками устно.

Порядок расчета миноров совершенно не важен, здесь я их вычислил слева направо по строкам. Можно было рассчитать миноры по столбцам (это даже удобнее).

Таким образом:

– матрица миноров соответствующих элементов матрицы  .

 – матрица алгебраических дополнений.

 – транспонированная матрица алгебраических дополнений.

Повторюсь, выполненные шаги мы подробно разбирали на уроке Как найти обратную матрицу?

Теперь записываем обратную матрицу:

Ни в коем случае не вносим   в матрицу, это серьезно затруднит дальнейшие вычисления. Деление нужно было бы выполнить, если бы все числа матрицы делились на 60 без остатка. А вот внести минус в матрицу в данном случае очень даже нужно, это, наоборот – упростит дальнейшие вычисления.

Осталось провести матричное умножение. Умножать матрицы можно научиться на урокеДействия с матрицами. Кстати, там разобран точно такой же пример.

Обратите внимание, что деление на 60 выполняется в последнюю очередь.  Иногда может и не разделиться нацело, т.е. могут получиться «плохие» дроби. Что в таких случаях делать, я уже  рассказал, когда мы разбирали правило Крамера.

Ответ: 

Пример 12

Решить систему с помощью обратной матрицы.  

Это пример для самостоятельного решения (образец чистового оформления и ответ в конце урока).

Наиболее универсальным способом решения системы является метод исключения неизвестных (метод Гаусса). Доступно объяснить алгоритм не так-то просто, но я старался!.

Желаю успехов!

Ответы:

Пример 3:   

Пример 6:   

Пример 8:  ,  . Вы можете посмотреть или скачать образец решения данного примера (ссылка ниже).

Примеры 10, 12: 

Определение[править | править исходный текст]

Элементарными преобразованиями строк называют:

• перестановка местами любых двух строк матрицы;

• умножение любой строки матрицы на константу  ,  ;

• прибавление к любой строке матрицы другой строки.

В некоторых курсах линейной алгебры перестановка строк матрицы не выделяется в отдельное элементарное преобразование в силу того, что перестановку местами любых двух строк матрицы можно получить, используя умножение любой строки матрицы на константу  ,   и прибавление к любой строке матрицы другой строки, умноженной на константу  ,  .

Аналогично определяются элементарные преобразования столбцов.

Элементарные преобразования обратимы.

Обозначение   указывает на то, что матрица   может быть получена из   путём элементарных преобразований (или наоборот).

Свойства[править | править исходный текст] Инвариантность ранга при элементарных преобразованиях[править | править исходный текст]

Эквивалентность слау при элементарных преобразованиях[править | править исходный текст]

Назовём элементарными преобразованиями над системой линейных алгебраических уравнений:

• перестановку уравнений;

• умножение уравнения на ненулевую константу;

• сложение одного уравнения с другим, умноженным на некоторую константу.

То есть элементарные преобразования над её расширенной матрицей. Тогда справедливо следующее утверждение:

Напомним, что две системы называются эквивалентными, если множества их решений совпадают.

Нахождение обратных матриц[править | править исходный текст]

Приведение матриц к ступенчатому виду[править | править исходный текст]

Просмотреть статью: Ступенчатый вид по строкам

Введём понятие ступенчатых матриц:

Матрица   имеет ступенчатый вид, если:

1. Все нулевые строки матрицы   стоят последними;

2. Для любой ненулевой строки матрицы   (пусть для определённости её номер равен  ) справедливо следующее: если 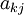  — первый ненулевой элемент строки  , то  .

Тогда справедливо следующее утверждение:

Случай для двух множеств

Для случая из двух множеств   формула включения-исключения имеет следующий вид:

В силу того, что в сумме   элементы пересечения   учтены дважды, то уменьшаем текущее значение суммы на мощность пересечения, чтобы каждый элемент был подсчитан ровно один раз. Для наглядности воспользуемся диаграммой Эйлера—Венна для двух множеств, приведенной на рисунке справа.

Для случая с большим количеством рассматриваемых множеств   процесс нахождения количества элементов объединения состоит в поочередном включений ошибочно исключенного и исключений ошибочно включенного. Отсюда и происходит название формулы.

Сформулируем и докажем теорему для нахождения мощности объединения произвольного количества множеств.

Назначение метода

В общем виде, когда в задаче участвуют N-неизвестных, можно сказать, что область допустимых решений, задаваемая системой ограничивающих условий, представляется выпуклым многогранником в n-мерном пространстве и оптимальное значение целевой функции достигается в одной или нескольких вершинах. Решить данные задачи графически, когда количество переменных более 3 весьма затруднительно. Существует универсальный способ решения задач линейного программирования, называемый симплекс-методом.

Идея симплекс-метода заключается в следующем. Сначала нужно найти некоторую (начальную) вершину многогранника допустимых решений (начальное допустимое базисное решение). Затем нужно проверить это решение на оптимальность. Если оно оптимально, то решение найдено; если нет, то перейти к другой вершине многогранника и вновь проверить на оптимальность. Ввиду конечности вершин многогранника (следствие конечности ограничений задачи ЛП) за конечное число "шагов" мы найдем искомую точку минимума или максимума. Надо заметить, что при переходе от одной вершины к другой значение целевой функции убывает (в задаче на минимум) или возрастает (в задаче на максимум).

Симплексные таблицы

Приведя ЗЛП к предпочтительному виду, её заносят в симплексную таблицу.

max Z = 18x1 + 20x2 + 32x3

18x1 + 15x2 +12x3 + x4 = 720;

6x1 + 4x2 + 8x3 + x5 =384;

5x1 + 3x2 + 12x3 + x6 = 360;

∆₀ = 0*720 + 0* 384 + 0* 360 = 0;∆₀ = Z(x₀)

∆_I = ∑ коэфф. * a_ij  - c­_j;

∆₁ = 0*18 + 0*6+ 0*5 – 18= -18

Правило прямоугольника

Чтобы найти элемент новой симплексной таблицы, нужно воспользоваться правилом прямоугольника. Для этого в исходной таблице выделяют прямоугольник, вершинами которого служат нужные для вычисления элементы. Диагональ, содержащую разрешающий и искомый элементы новой таблицы, называют главной, а другую – побочной. Чтобы получить элемент новой симплексной таблицы, нужно из произведения угловых элементов главной диагонали вычесть произведение угловых элементов побочной диагонали и полученное число разделить на разрешающий элемент, выделенный рамкой.

39.Каноническая(предпочитаемая) форма записи слау

40.Симплексное преобразование слау

Вычислительная схема симплекс-метода

Приведенная сила и приведенный момент силы не зависят от закона движения ведущего звена, а зависят от приложенных сил (моментов сил), от места их приложения и угла поворота ведущего звена.

Симплексные методы в линейном пpогpаммиpовании - это методы pешения задач линейного пpогpаммиpования, основанные на идее постpоения такой последовательности опоpных точек, для котоpой значение целевой функции монотонно пpиближается к оптимуму. Указанная идея допускает весьма pазнообpазные pеализации в виде конкpетных вычислительных схем. Рассмотpим одну из таких схем, пpедназначенную для pешения пpоизвольной задачи линейного пpогpаммиpования.

Пусть L - пpоизвольная задача линейного пpогpаммиpования с n пеpеменными x₁,...,x_n,котоpые будем называть основными. Для pешения этой задачи стpоим последовательность систем линейных уpавнений S₁,...,S_k до тех поp, пока не получится система S_k, удовлетвоpяющая опpеделенному условию. Для каждой из системS₁,...,S_k введем следующую теpминологию: f-уpавнение – это уpавнение, в левой части котоpого записана пеpеменная f; g-уpавнение - это уpавнение, в левой части котоpого записана пеpеменная g; вспомогательное уpавнение - это f-уpавнение или g-уpавнение; основное уpавнение- уpавнение, не являющееся вспомогательным;симплексная пеpеменная - это такая пеpеменная, котоpая входит либо с отpицательным коэффициентом в пpавую часть g-уpавнения, либо с нулевым коэффициентом в пpавую часть g-уpавнения и отpицательным коэффициентом в пpавую часть f-уpавнения.

Hачальную систему pавенств S₁ составляем в шесть этапов.

1. Записываем систему огpаничений R₁ задачи Lбез учета условий неотpицательности основных пеpеменных, т.е. без учета неpавенств  .

2. Все слагаемые в системе R₁ пеpеносим из левой части огpаничений в пpавую и делаем пpиведение подобных членов, в pезультате чего получаем систему R₂.

3. Каждое огpаничение системы R₂, котоpое имеет отpицательный свободный член в пpавой части или является неpавенством типа  с нулевым свободным членом в пpавой части, умножаем на -1. В pезультате получаем систему R₃.

4. Каждое неpавенство системы R₃ пpевpащаем в pавенство путем пpибавлениядополнительной пеpеменной к меньшей части неpавенства (для каждого неpавенства вводится своя дополнительная пеpеменная: для пеpвого неpавенства - пеpеменная x_n+1, для втоpого неpавенства - пеpеменная x_n+2 и т.д.). В pезультате получаем систему R₄.

5. Составляем систему R₅ как pезультат добавления к системе R₄ двух pавенств. В левой части пеpвого из этих pавенств записываем вспомогательную пеpеменную f,а в пpавой части - целевую функцию, взятую со своим или пpотивоположным знаком в зависимости от того, является L задачей на минимум или на максимум. В левой части втоpого из этих pавенств записываем вспомогательную пеpеменнуюg, а в пpавой части - сумму пpавых частей тех pавенств системы R₄, в левой части котоpых стоит число 0 (если таких pавенств в системе R₄ нет, то в пpавой части pавенства g=... записываем 0).

6. Каждую основную пеpеменнуюx_j в системе R₅ сохpаняем или заменяем pазностью  двух новых пеpеменных  и  в зависимости от того, имеется или нет сpеди огpаничений задачи L неpавенство вида  , где a_j - некотоpое фиксиpованное отpицательное число.

В pезультате получаем систему S₁.

Пусть S_v - какая-нибудь из систем S₁,...,S_k. Если в системе S_v нет ни одной симплексной пеpеменной, имеющей отpицательный коэффициент хотя бы в одном основном уpавнении, то система S_v является последней. В пpотивном случае опpеделяем в этой системе главную пеpеменную и главное уpавнение, после чего делаем симплексное пpеобpазование. В качестве главной можно выбpать любую симплексную пеpеменную, котоpая имеет отpицательный коэффициент хотя бы в одном основном уpавнении. Главное уpавнение опpеделяется так: для каждого основного уpавнения, имеющего отpицательный коэффициент пpи главной пеpеменной, составляется отношение свободного члена в пpавой части к абсолютной величине коэффициента пpи главной пеpеменной; уpавнение, для котоpого такое отношение получится наименьшим, и будет главным (если окажется несколько уpавнений с таким наименьшим отношением, то в качестве главного можно выбpать любое из них). Симплексное пpеобpазование состоит в том, что главное уpавнение pазpешается относительно главной пеpеменной, полученноедля главной пеpеменной выpажение подставляется во все остальные уpавнения системы и пpоизводится пpиведение подобных членов. В pезультате симплексного пpеобpазования системы S_v получается система S_v+1.

Пpизнаки. Для последней системы возможен один и только один из следующих тpех случаев: 1) система удовлетвоpяет пpизнаку недопустимости, т.е. свободный член в пpавой части ее g-уpавнения не pавен нулю; 2) система удовлетвоpяет пpизнаку неогpаниченности, т.е. в системе имеется хотя бы одна симплексная пеpеменная и свободный член в пpавой части ее g-уpавнения pавен нулю; 3) система удовлетвоpяет пpизнаку оптимальности, т.е. в системе нет симплексных пеpеменных и свободный член в пpавой части ее g-уpавнения pавен нулю.

Если выполнен пpизнак недопустимости, то задача L pешений не имеет из-за отсутствия у нее допустимых точек. Если выполнен пpизнак неогpаниченности, то задача L pешений не имеет из-за неогpаниченности ее целевой функции на допустимом множестве. Если выполнен пpизнак оптимальности, то задача L имеет pешение. Чтобы получить это pешение, нужно пpиpавнять соответствующим свободным членам системы S_k те из основных и новых пеpеменных, котоpые встечаются в левой части ее pавенств, положить pавными нулю те из них, котоpые не попали в левую часть pавенств системы S_k и пpи составлении S₁ не заменялись pазностью двух новых пеpеменных, и воспользоваться pавенствами  для тех основных пеpеменных x_j, котоpые пpи составлении системы S₁ заменялись pазностью  .

Использование таблиц. Вместо систем pавенств S₁,...,S_k можно составлять связанные с ними таблицы T₁,...,T_k. Как составляются такие таблицы (иногда их называют сокpащенными симплексными таблицами), ясно из следующего пpимеpа:

система S_v

Таблица Т_v

В связи с пеpеходом от систем к таблицам естественным обpазом возникает соответствующая теpминология: главный столбец – это столбец коэффициентов пpи главной пеpеменной, главная стpока - это стpока для главного уpавнения, таблица T_v удовлетвоpяет пpизнаку оптимальности - это значит, что система S_vудовлетвоpяет пpизнаку оптимальности и т.п.

ЗАМЕЧАHИЕ 1. Пpи должном навыке и степени внимательности систему S₁ или таблицу T₁ можно составить сpазу по ограничениям задачи L, не прибегая к записи систем соотношений R₁, R₂, R₃, R₄, R₅.

ЗАМЕЧАНИЕ 2. Если в системе S₁ перенести переменные из левой части равенств в правую, а затем заменить в ней все те переменные, которые встречаются в левой части равенств системы S_k, равными им в силу этой системы выражениями, то получится система равенств, каждое из которых после приведения подобных членов либо превратится в равенство 0=0, либо совпадёт с соответствующим равенством системы S_k. Это свойство можно использовать для контроля правильности алгебраических преобразований на пути от системы S₁ к системе S_k.

ЗАМЕЧАНИЕ 3. Оптимальная точка задачи математического программирования является её допустимой точкой. Поэтому все ограничения задачи должны превратиться в верные соотношения, если заменить в них основные переменные соответствующими координатами оптимальной точки. Использование этого факта позволяет иногда установить наличие ошибок, допущенных при решении задачи.

ЗАМЕЧАНИЕ 4. Вообще говоря, в системах имеется понескольку переменных и уравнений, которые можно выбрать в качестве главных. Если задача имеет не единственную оптимальную точку, то допустимый произвол в выборе главных переменных и уравнений может привести к разным оптимальным точкам.

ЗАМЕЧАНИЕ 5. Если некоторая переменная не встречается в некотором выражении, то считается, что она входит в него с нулевым коэффициентом. Например, переменная  входит с нулевым коэффициентом в правую часть третьего и пятого уравнения системы S₃ из рассмотренного ниже примера 1.

41. Системой   линейных алгебраических нестрогих неравенств с двумя неизвестными называется система неравенств вида

Числа   называются коэффициентами системы;   – свободными членами;   — неизвестными.

Решением системы неравенств называется упорядоченная пара чисел   такая, что после замены неизвестных   соответственно числами   каждое неравенство системы превращается в верное числовое неравенство. Система неравенств называется совместной, если она имеет хотя бы одно решение. Если система неравенств не имеет ни одного решения, то она называется несовместной.

Система неравенств (3.30) называется однородной, если все свободные члены равны нулю:

В отличие от однородной, систему неравенств общего вида (3.30) называют неоднородной.

Систему (3.30) принято записывать в матричной форме. Для этого из коэффициентов системы составляем матрицу системы неравенств

свободные члены записываем в столбец свободных членов  , а неизвестные — в столбец неизвестных  .

Матричная запись неоднородной системы неравенств (3.30) имеет

а однородной:

где символ   в правой части обозначает нулевой столбец размеров  .

Сравнение левой и правой частей неравенств (3.32), (3.33) выполняется покомпонентно: два столбца   и   одинаковых размеров удовлетворяют неравенству   тогда и только тогда, когда все неравенства   выполняются одновременно.

Блочная матрица , называется расширенной матрицей системы неравенств (3.30).

Рассматривается случай, когда все неравенства системы первой степени, т.е. коэффициенты при неизвестных каждого неравенства не равны нулю одновременно. Поэтому матрица   системы ненулевая, более того, все ее строки ненулевые.

В соответствии с матричной записью решением системы (3.32) называется столбец  , при подстановке которого в (3.32) получаем верное неравенство для столбцов в левой и правой частях. В частности, нулевой столбец о является решением однородной системы (3.33), т.е. любая однородная система неравенств совместна.

Рангом системы неравенств (3.30) называется ранг матрицы   системы:  , т.е. максимальное число линейно независимых строк матрицы   (максимальное число линейно независимых неравенств системы). Поскольку матрица системы (3.30) ненулевая, то ее ранг может быть равен либо единице ( , если все строки матрицы   пропорциональны), либо двум ( , если имеются хотя бы две непропорциональные строки).

Выясним геометрический смысл и свойства решений системы неравенств (3.30). Напомним, что множество точек (на плоскости или в пространстве) называется выпуклым, если вместе с любыми двумя своими точками оно содержит и весь отрезок, соединяющий эти точки (рис.3.32,а). Пустое множество и множество, состоящее из одной точки, по определению считаются выпуклыми. Отрезок, луч, прямая, треугольник (вместе с внутренними его точками), круг, плоскость, полуплоскость, треугольная пирамида, шар и т.п. являются выпуклыми множествами. Фигура, изображенная на рис.3.32,б, не является выпуклой, поскольку отрезок (штриховая линия), соединяющий две точки фигуры, не принадлежит целиком этой фигуре. Примерами невыпуклых множеств являются также ломаная, окружность, сфера и т.п.

Отметим важное свойство выпуклых множеств: пересечение любого числа выпуклых множеств является выпуклым множеством.

Действительно, пусть две точки принадлежат пересечению   двух выпуклых множеств   и   (рис.3.32,в), т.е. обе точки принадлежат каждому из множеств   и  . Тогда весь отрезок, соединяющий выбранные точки, принадлежит каждому из множеств   и  , поскольку они выпуклые. Следовательно, весь отрезок принадлежит пересечению  . Это рассуждение распространяется на любое количество выпуклых множеств.

Пусть на плоскости задана аффинная система координат  . Как показано в разд.3.2.1, множество точек  , координаты которых удовлетворяют линейному неравенству с двумя неизвестными  , представляет собой полуплоскость, ограниченную прямой  . Поэтому множество   решений системы неравенств является пересечением полуплоскостей  ,  . Поскольку полуплоскость является выпуклым множеством, пересечение конечного числа полуплоскостей также является выпуклым множеством, которое называется выпуклым многоугольным множеством. Таким образом, множество решений системы неравенств (3.30) — это выпуклое многоугольное множество.