35. Векторная и матричная формы записи систем линейных уравнений Векторная форма записи

Система уравнений может быть записана в векторном виде:

A₁x₁ + A₂x₂ + ... + A_nx_n =B

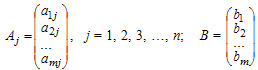
Пример 1. Записать в векторном виде.

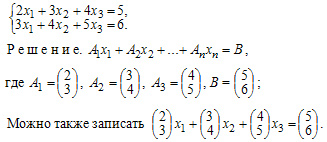
Матричная форма записи

В матричной записи система линейных уравнений может быть записана следующим образом:

AX=B

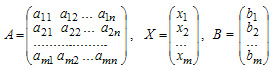
Пример 2: Записать в матричном виде систему из предыдущего примера

36.Решение слау методом гаусса

Метод Гаусса применим для решения системы линейных алгебраических уравнений c невырожденной матрицей системы. Идея метода Гаусса состоит в том, что систему n линейных алгебраических уравнений относительно nнеизвестных x₁ , x₂ , ..., x_n

приводят последовательным исключением неизвестных к эквивалентной системе с треугольной матрицей

решение которой находят по рекуррентным формулам:

x_n =d_n , x_i = d_i -S ⁿ_k=i+1 c_ik x_k , i=n-1, n-2, ...,1.

Матричная запись метода Гаусса.

1. Прямой ход метода Гаусса: приведение расширенной матрицы системы

     к ступенчатому виду

             с помощью элементарных операций над строками матрицы (под элементарными операциями понимаются следующие операции:

• перестановка строк;

• умножение строки на число, отличное от нуля;

• сложение строки матрицы с другой строкой, умноженной на отличное от нуля чиcло).