Метод Гаусса—Жордана[править | править исходный текст]

Возьмём две матрицы: саму A и единичную E. Приведём матрицу A к единичной матрице методом Гаусса—Жордана. После применения каждой операции к первой матрице применим ту же операцию ко второй. Когда приведение первой матрицы к единичному виду будет завершено, вторая матрица окажется равной A⁻¹.

При использовании метода Гаусса первая матрица будет умножаться слева на одну из элементарных матриц   (трансвекцию или диагональную матрицу с единицами на главной диагонали, кроме одной позиции):

.

.

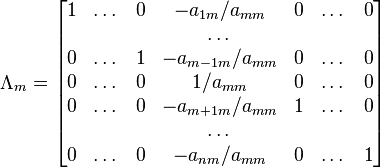Вторая матрица после применения всех операций станет равна  , то есть будет искомой. Сложность алгоритма —  .

С помощью матрицы алгебраических дополнений[править | править исходный текст]

где   — присоединенная матрица;

Полученная матрица A⁻¹ и будет обратной. Сложность алгоритма зависит от сложности алгоритма расчета определителя O_det и равна O(n²)·O_det.

Использование lu/lup-разложения[править | править исходный текст]

Матричное уравнение   для обратной матрицы   можно рассматривать как совокупность   систем вида  . Обозначим  -ый столбец матрицы   через  ; тогда  ,  ,поскольку  -м столбцом матрицы   является единичный вектор  . другими словами, нахождение обратной матрицы сводится к решению n уравнений с одной матрицей и разными правыми частями. После выполнения LUP-разложения (время O(n³)) на решение каждого из n уравнений нужно время O(n²), так что и эта часть работы требует времени O(n³)^[1].

Если матрица A невырождена, то для неё можно рассчитать LUP-разложение  . Пусть  ,  . Тогда из свойств обратной матрицы можно записать:  . Если умножить это равенство на U и L то можно получить два равенства вида   и  . Первое из этих равенств представляет собой систему из n² линейных уравнений для   из которых известны правые части (из свойств треугольных матриц). Второе представляет также систему из n² линейных уравнений для   из которых известны правые части (также из свойств треугольных матриц). Вместе они представляют собой систему из n² равенств. С помощью этих равенств можно реккурентно определить все n² элементов матрицы D. Тогда из равенства (PA)⁻¹ = A⁻¹P⁻¹ = B⁻¹ = D. получаем равенство  .

В случае использования LU-разложения не требуется перестановки столбцов матрицы D но решение может разойтись даже если матрица A невырождена.

Сложность алгоритма — O(n³).

33.Элементарными преобразованиями матрицы

называются следующие:

1) перестановка строк (столбцов);

2) умножение строки (столбца) на число, отличное от нуля;

3) прибавление к элементам строки (столбца) соответсвующих элементов другой строки (столбца), предварительно умноженных на некоторое число.

 

Пусть в матрице A размера m×n выбраны произвольно k строк и k столбцов (k≤min(m,n)). Элементы, стоящие на пересечении выбранных строк и столбцов, образуют квадратную матрицу порядка k, определитель которой называется минором k−го порядка матрицы A.

Максимальный порядок r отличных от нуля миноров матрицы A называется ее рангом, а любой минор порядка r, отличный от нуля - базисным минором.

Основные методы вычисления ранга матрицы:

Метод окаймляющих миноров. Пусть в матрице найден минор k-го порядка M,отличный от нуля. Рассмотрим лишь те миноры (k+1)− го порядка, которые содержат в себе (окаймляют) минор M: если все они равны  нулю, то ранг матрицы равен k. В противном случае среди окаймляющих миноров найдется ненулевой минор (k+1)−го порядка, и вся процедура повторяется.

Метод элементарных преобразований основан на том, что элементарные преобразования матрицы не меняют ее ранга. Используя эти преобразования матрицу можно привести к такому виду, когда все ее элементы кроме a11,a22,...,arr (r≤min(m,n)), равны нулю. Следовательно, ранг матрицы равен r.

Ранг матрицы

Определение

Рангом матрицы   называется ранг её системы строк или столбцов.

Обозначается 

На практике для нахождения ранга матрицы используют следующее утверждение: ранг матрицы равен количеству ненулевых строк после приведения матрицы к ступенчатому виду.

Элементарные преобразования над строками (столбцами) матрицы не меняют её ранга.

Ранг ступенчатой матрицы равен количеству её ненулевых строк.

Пример

Задание. Найти ранг матрицы 

Решение. С помощью элементарных преобразований над ее строками приведем матрицу   к ступенчатому виду. Для этого вначале от третьей строки отнимем две вторых:

От второй строки отнимаем четвертую строку, умноженную на 4; от третьей - две четвертых:

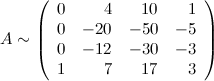
Ко второй строке прибавим пять первых, к третьей - три третьих:

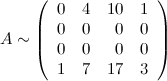
Меняем местами первую и вторую строчки:

Далее четвертую и первую строки:

Ответ. 

Метод окаймления миноров

Теорема

Ранг матрицы равен наибольшему порядку отличного от нуля минору.

На этой теореме базируется еще один метод нахождения ранга матрицы - метод окаймления миноров. Суть этого метода заключается в нахождении миноров, начиная с низших порядков и двигаясь к более высоким. Если минор  -го порядка не равен нулю, а все миноры  -го равны нулю, то ранг матрицы будет равен   .

Пример

Задание. Найти ранг матрицы 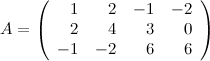  , используя метод окаймления миноров.

Решение. Минорами минимального порядка являются миноры первого порядка, которые равны элементам матрицы   . Рассмотрим, например, минор   . расположенный в первой строке и первом столбце. Окаймляем его с помощью второй строки и второго столбца, получаем минор  ; рассмотрим еще один минор второго порядка, для этого минор   окаймляем при помощи второй строки и третьего столбца, тогда имеем минор   , то есть ранг матрицы не меньше двух. Далее рассматриваем миноры третьего порядка, которые окаймляют минор   . Таких миноров два: комбинация третьей строки со вторым столбцом или с четвертым столбцом. Вычисляем эти миноры:

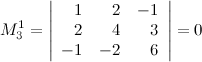
так как содержит два пропорциональных столбца (первый и второй); второй минор

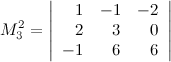
преобразуем следующим образом: к первой строке прибавим третью, а ко второй две третьих:

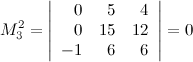
И так как первая и вторая строки пропорциональны, то минор равен нулю.

Таким образом, все окаймляющие миноры третьего порядка равны нулю. А, значит, ранг матрицы  равен двум: 

Ответ. 

34. Системой линейных алгебраических уравнений (СЛАУ) называется система вида:

Упорядоченный набор значений   называется решением системы, если при подстановке в уравнения все уравнения превращаются в тождество.

1. Если количество уравнений в системе больше количества неизвестных, то система называется переобусловленной. Если количество уравнений меньше количества неизвестных, то система называется недообусловленной. 2. Если система имеет хотя бы одно решение, она называется совместной. Система, не имеющая решений, называется несовместной. 3. Совместная система, имеющая единственное решение, называется определенной. Совместная система, имеющая бесконечное количество решений, называется неопределенной. 4. Если все коэффициенты правых частей системы равны нулю, то система называется однородной. Если хотя бы один из этих коэффициентов не равен нулю, то система называется неоднородной. Однородная система уравнений всегда совместна, т.к. имеет хотя бы одно решение, x_i = 0 (i=1,2,…,n), называемое тривиальным.