29.Система единичных векторов,свойства,базис,разложение по данному базису
Единичный вектор - это вектор, абсолютная величина (модуль) которого равен единице. Для обозначения единичного вектора мы будем использовать нижний индекс е. Так, если задан вектор а, то его единичным вектором будет вектор ае. Этот единичный вектор направлен туда же, куда направлен и сам вектор а, и его модуль равен единице, то есть ае = 1. Очевидно, а = а·ае (а - модуль вектора а). Это следует из правила, по которому выполняется операция умножения скаляра на вектор. Единичные векторы часто связывают с координатными осями системы координат (в частности, с осями декартовой системы координат). Направления этих векторов совпадают с направлениями соответствующих осей, а их начала часто совмещают с началом системы координат. Напомню, что декартовой системой координат в пространстве традиционно называется тройка взаимно перпендикулярных осей, пересекающихся в точке, которая называется началом координат. Координатные оси обычно обозначают буквами X , Y , Z и называют соответственно осью абсцисс, осью ординат и осью аппликат. Сам Декарт пользовался только одной осью, на которой откладывались абсциссы. Заслуга использования системы осей принадлежит его ученикам. Поэтому фраза декартова система координат исторически ошибочна. Лучше говорить прямоугольная система координат илиортогональная система координат. Тем не менее, изменять традиции мы не станем и в дальнейшем будем считать, что декартова и прямоугольная (ортогональная) системы координат - это одно и то же. Единичный вектор, направленный вдоль оси Х, обозначается i, единичный вектор, направленный вдоль оси Y , обозначается j, а единичный вектор, направленный вдоль оси Z, обозначается k. Векторыi, j, k называются ортами (рис. 12, слева), они имеют единичные модули, то есть i = 1, j = 1, k = 1.
Рис. 12
Оси и орты прямоугольной системы координат в некоторых случаях имеют другие названия и обозначения. Так, ось абсцисс X может называться касательной осью, а ее орт обозначается τ(греческая строчная буква тау), ось ординат – осью нормали, ее орт обозначается n , ось аппликат – осью бинормали, ее орт обозначается b. Зачем менять названия, если суть остается той же? Дело в том, что, например, в механике при изучении движения тел прямоугольная система координат используется очень часто. Так вот, если сама система координат неподвижна, а изменение координат движущегося объекта отслеживается в этой неподвижной системе, то обычно оси обозначают X, Y, Z, а их орты соответственно i, j, k. Но нередко, когда объект движется по какой-то криволинейной траектории (например, по окружности) бывает удобнее рассматривать механические процессы в системе координат, движущейся с этим объектом. Именно для такой движущейся системы координат и используются другие названия осей и их ортов. Просто так принято. В этом случае ось X направляют по касательной к траектории в той ее точке, в которой в данный момент этот объект находится. И тогда эту ось называют уже не осью X, а касательной осью, а ее орт обозначают уже не i, а τ. Ось Y направляют по радиусу кривизны траектории (в случае движения по окружности – к центру окружности). А поскольку радиус перпендикулярен касательной, то ось называют осью нормали (перпендикуляр и нормаль – это одно и то же). Орт этой оси обозначают уже не j, а n. Третья ось (бывшая Z) перпендикулярна двум предыдущим. Это – бинормаль с ортом b (рис. 12, справа). Кстати, в этом случае такую прямоугольную систему координат часто называют «естественной» или натуральной.
п.1. Базис на прямой, на плоскости и в пространстве.
Определение.
Любое конечное множество векторов 
называется
системой векторов.
Определение.
Выражение 
,
где 
называется
линейной комбинацией системы векторов
,
ачисла 
называются
коэффициентами этой линейной комбинации.
Пусть
L, Р и S – прямая, плоскость и
пространство точексоответственно
и 
.
Тогда 
– векторные пространствавекторов как
направленных отрезков на прямой L,
на плоскости Р
и впространстве S
соответственно.
Определение.
Базисом векторного пространства 
называется
любой ненулевой вектор 
,
т.е. любой ненулевой вектор
коллинеарныйпрямой L: 
и 
.
Обозначение
базиса
: 
–
базис
.
Определение.
Базисом векторного пространства 
называется
любая упорядоченная пара
неколлинеарных векторов пространства
.
рис.1.
,
где 
, 
–
базис
.
Определение.
Базисом векторного пространства 
называется
любая упорядоченная тройка
некомпланарных векторов (т.е.
не лежащих в одной плоскости) пространства
.
рис.2.
–
базис
.
Замечание. Базис векторного пространства не может содержать нулевого вектора: в пространстве по определению, в пространстве двавектора будут коллинеарные, если хотя бы один из них нулевой, впространстве три вектора будут компланарные, т.е будут лежать в одной плоскости, если хотя бы один из трех векторов будет нулевой.
п.2. Разложение вектора по базису.
Определение.
Пусть 
–
произвольный вектор,
–
произвольная система векторов.
Если выполняется равенство
,
(1)
то говорят, что вектор представлен в виде линейной комбинации данной системы векторов. Если данная система векторов является базисом векторного пространства, то равенство (1) называется разложением вектора по базису . Коэффициенты линейной комбинации называются в этом случае координатами вектора относительно базиса .
Теорема. (О разложении вектора по базису.)
Любой вектор векторного пространства можно разложить по его базису и притом единственным способом.
Доказательство.
1) Пусть L произвольная прямая (или ось)
и
–базис
.
Возьмем произвольный вектор 
.
Так как оба вектора 
и
коллинеарные
одной и той же прямой L,
то 
.
Воспользуемся теоремой о
коллинеарности двух векторов.
Так как
,
то найдется (существует) такое число 
,
что 
и
тем самым мы получили разложение
вектора
по
базису
векторного пространства
.
Теперь докажем единственность такого разложения. Допустим противное. Пусть имеется два разложения вектора по базису векторного пространства :
и 
,
где 
.
Тогда 
и
используя закон дистрибутивности,
получаем:
.
Так
как
,
то из последнего равенства следует,
что 
,
ч.т.д.
2)
Пусть теперь Р произвольная плоскость и
– базис
.
Пусть 
произвольный
вектор этой плоскости. Отложим все три
вектора от какой-нибудь одной точки
этой плоскости. Построим 4 прямых.
Проведемпрямую 
,
на которой лежит вектор
, прямую 
,
на которой лежит вектор 
.
Через конец вектора
проведем прямую параллельную
вектору
и
прямую параллельную вектору
.
Эти 4 прямые высекают
параллелограмм. См. ниже рис. 3. По правилу
параллелограмма 
,
и 
, 
,
– базис
, 
– базис
.
Теперь,
по уже доказанному в первой части этого
доказательства, существуют такие числа 
,
что
и 
.
Отсюда получаем:
и
возможность разложения по базису
доказана.
рис.3.
Теперь
докажем единственность разложения по
базису. Допустим противное. Пусть имеется
два разложения вектора
по
базису
векторного пространства
: 
и 
.
Получаем равенство
,
откуда следует 
.
Если 
,
то 
,
а т.к. 
,
то 
и
коэффициенты разложения равны: 
, 
.
Пусть теперь 
.
Тогда 
,
где 
.
По теореме о коллинеарностидвух векторов отсюда
следует, что 
.
Получили противоречие условию теоремы.
Следовательно,
и
,
ч.т.д.
3)
Пусть
– базис
и
пусть 
произвольный
вектор. Проведем следующие построения.
Отложим
все три базисных вектора 
и
вектор
от
одной точки и построим 6 плоскостей:
плоскость, в которой лежат
базисные векторы 
, плоскость 
и плоскость 
;
далее через конец вектора
проведем
три плоскости параллельно
только что построенным трем плоскостям.
Эти 6 плоскостей высекают
параллелепипед:
рис.4.
По правилу сложения векторов получаем равенство:
.
(1)
По
построению 
.
Отсюда, по теореме о коллинеарности двухвекторов,
следует, что существует число 
,
такое что 
.
Аналогично,
и 
,
где 
.
Теперь, подставляя эти равенства в (1),
получаем:
(2)
и возможность разложения по базису доказана.
Докажем единственность такого разложения. Допустим противное. Пусть имеется два разложения вектора по базису :
и 
.
Тогда
.
(3)
Заметим, что по условию векторы некомпланарные, следовательно, они попарно неколлинеарные.
Возможны два случая: или .
а) Пусть , тогда из равенства (3) следует:
.
(4)
Из
равенства (4) следует, что вектор
раскладывается
по базису 
,
т.е. вектор
лежит
в плоскости векторов
и,
следовательно, векторы
компланарные,
что противоречит условию.
б)
Остается случай
,
т.е. 
.
Тогда из равенства (3) получаем 
или
.
(5)
Так
как
– базис пространства векторов лежащих
в плоскости, а мы уже доказали единственность
разложения по базису векторов плоскости,
то из равенства (5) следует, что
и 
,
ч.т.д.
Теорема доказана.
1) Существует взаимно однозначное соответствие между множествомвекторов векторного пространства и множеством действительныхчисел R.
2)
Существует взаимно однозначное
соответствие между множествомвекторов векторного пространства
и
декартовым квадратом 
множества
действительных чисел R.
3)
Существует взаимно однозначное
соответствие между множествомвекторов векторного пространства
и
декартовым кубом 
множества
действительных чисел R.
Доказательство. Докажем третье утверждение. Первые два доказываются аналогично.
Выберем
и зафиксируем в пространстве
какой-нибудь базис
и
устроим отображение 
по
следующему правилу:
,
(6)
т.е. каждому вектору поставим в соответствие упорядоченный набор его координат.
Так как при фиксированном базисе каждый вектор имеет единственный набор координат, то соответствие, задаваемое правилом (6) действительно является отображением.
Из доказательства теоремы следует, что различные векторы имеют различные координаты относительно одного и того же базиса, т.е.отображение (6) является инъекцией.
Пусть 
произвольный
упорядоченный набор действительных
чисел.
Рассмотрим
вектор 
.
Этот вектор по построению имеет координаты
.
Следовательно, отображение (6)
является сюръекцией.
Отображение, которое одновременно инъективное и сюръективное является биективным, т.е. взаимно однозначным, ч.т.д.
Следствие доказано.
Теорема. (О равенстве двух векторов.)
Два вектора равны тогда и только тогда, когда равны их координатыотносительно одного и того же базиса.
Доказательство сразу же вытекает из предыдущего следствия.
30. Матрицы. Действия над матрицами. Свойства операций над матрицами. Виды матриц.
Матрицы (и соответственно математический раздел - матричная алгебра) имеют важное значение в прикладной математике, так как позволяют записать в достаточно простой форме значительную часть математических моделей объектов и процессов. Термин "матрица" появился в 1850 году. Впервые упоминались матрицы еще в древнем Китае, позднее у арабских математиков.
Матрицей A=Amn порядка m*n называется прямоугольная таблица чисел, содержащая m - строк и n - столбцов.
Элементы матрицы aij, у которых i=j, называются диагональными и образуют главную диагональ.
Для квадратной матрицы (m=n) главную диагональ образуют элементы a11, a22,..., ann .
Равенство матриц.
A=B, если порядки матриц A и B одинаковы и aij=bij (i=1,2,...,m; j=1,2,...,n)
Действия над матрицами.
1. Сложение матриц - поэлементная операция
2. Вычитание матриц - поэлементная операция
3. Произведение матрицы на число - поэлементная операция
4. Умножение A*B матриц по правилу строка на столбец (число столбцов матрицы А должно быть равно числу строк матрицы B)
Amk*Bkn=Cmn причем каждый элемент сij матрицы Cmn равен сумме произведений элементов i-ой строки матрицы А на соответствующие элемеенты j-го столбца матрицы B , т.е.
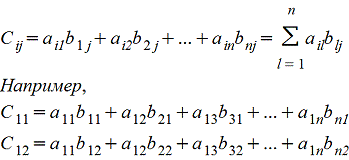
Покажем операцию умножения матриц на примере
5. Возведение в степень
m>1 целое положительное число. А - квадратная матрица (m=n) т.е. актуально только для квадратных матриц
6. Транспонирование матрицы А. Транспонированную матрицу обозначают AT или A'
Строки и столбцы поменялись местами
Пример
Свойства опрераций над матрицами
A+B=B+A
(A+B)+C=A+(B+C)
λ(A+B)=λA+λB
A(B+C)=AB+AC
(A+B)C=AC+BC
λ(AB)=(λA)B=A(λB)
A(BC)=(AB)C
(A')'=A
(λA)'=λ(A)'
(A+B)'=A'+B'
(AB)'=B'A'
Виды матриц
1. Прямоугольные: m и n - произвольные положительные целые числа
2. Квадратные: m=n
3. Матрица строка: m=1. Например, (1 3 5 7 ) - во многих практических задачах такая матрица называется вектором
4. Матрица столбец: n=1. Например
5. Диагональная матрица: m=n и aij=0, если i≠j. Например
6. Единичная матрица: m=n и
7. Нулевая матрица: aij=0, i=1,2,...,m
j=1,2,...,n
8. Треугольная матрица: все элементы ниже главной диагонали равны 0.
Пример.
9. Симметрическая матрица: m=n и aij=aji (т.е. на симметричных относительно главной диагонали местах стоят равные элементы), а следовательно A'=A
Например,
10. Кососимметрическая матрица: m=n и aij=-aji (т.е. на симметричных относительно главной диагонали местах стоят противоположные элементы). Следовательно, на главной диагонали стоят нули (т.к. при i=j имеем aii=-aii)
Пример.
Ясно, A'=-A
11. Эрмитова матрица: m=n и aii=-ãii (ãji - комплексно - сопряженное к aji, т.е. если A=3+2i, то комплексно - сопряженное Ã=3-2i)
Пример
Теперь переходим непосредственно к изучению действий с матрицами:
1) Действие первое. Вынесение минуса из матрицы (внесение минуса в матрицу).
Вернемся
к нашей матрице 
.
Как вы наверняка заметили, в данной
матрице слишком много отрицательных
чисел. Это очень неудобно с точки зрения
выполнения различных действий с матрицей,
неудобно писать столько минусов, да и
просто в оформлении некрасиво выглядит.
Вынесем
минус за пределы матрицы, сменив у
КАЖДОГО элемента матрицы знак:
У
нуля, как Вы понимаете, знак не меняется,
ноль – он и в Африке ноль.
Обратный
пример: 
.
Выглядит безобразно.
Внесем минус в матрицу, сменив у КАЖДОГО элемента матрицы знак:
Ну вот, гораздо симпатичнее получилось. И, самое главное, выполнять какие-либо действия с матрицей будет ПРОЩЕ. Потому-что есть такая математическая народная примета: чем больше минусов – тем больше путаницы и ошибок.
2) Действие второе. Умножение матрицы на число.
Пример:
Всё просто, для того чтобы умножить матрицу на число, нужно каждый элемент матрицы умножить на данное число. В данном случае – на тройку.
Еще один полезный пример:
–
умножение
матрицы на дробь
Сначала
рассмотрим то, чего делать НЕ
НАДО:
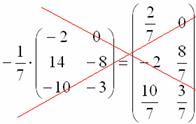Вносить
дробь в матрицу НЕ НУЖНО, во-первых, это
только затрудняет дальнейшие действия
с матрицей, во-вторых, затрудняет проверку
решения преподавателем (особенно,
если
–
окончательный ответ задания).
И, тем более, НЕ НАДО делить каждый элемент матрицы на минус семь:
Из статьи Математика для чайников или с чего начать, мы помним, что десятичных дробей с запятой в высшей математике стараются всячески избегать.
Единственное, что желательно сделать в этом примере – это внести минус в матрицу:
А вот если бы ВСЕ элементы матрицы делились на 7 без остатка, то тогда можно (и нужно!) было бы поделить.
Пример:
В
этом случае можно и НУЖНО умножить
все элементы матрицы на 
,
так как все числа матрицы делятся на
2 без
остатка.
Примечание: в теории высшей математики школьного понятия «деление» нет. Вместо фразы «это поделить на это» всегда можно сказать «это умножить на дробь». То есть, деление – это частный случай умножения.
3) Действие третье. Транспонирование матрицы.
Для того чтобы транспонировать матрицу, нужно ее строки записать в столбцы транспонированной матрицы.
Пример:
Транспонировать
матрицу 
Строка здесь всего одна и, согласно правилу, её нужно записать в столбец:
–
транспонированная
матрица.
Транспонированная
матрица обычно обозначается надстрочным
индексом 
или
штрихом справа вверху.
Пошаговый пример:
Транспонировать матрицу
Сначала переписываем первую строку в первый столбец:
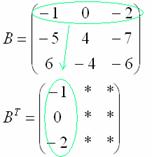
Потом
переписываем вторую строку во второй
столбец:
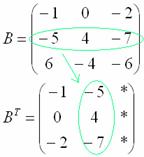
И, наконец, переписываем третью строку в третий столбец:
Готово. Грубо говоря, транспонировать – это значит повернуть матрицу набок.
4) Действие четвертое. Сумма (разность) матриц.
Сумма матриц действие несложное. НЕ ВСЕ МАТРИЦЫ МОЖНО СКЛАДЫВАТЬ. Для выполнения сложения (вычитания) матриц, необходимо, чтобы они были ОДИНАКОВЫМИ ПО РАЗМЕРУ.
Например,
если дана матрица «два на два», то ее
можно складывать только с матрицей «два
на два» и никакой другой!
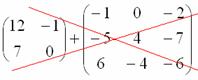
Пример:
Сложить
матрицы 
и 
Для того чтобы сложить матрицы, необходимо сложить их соответствующие элементы:
Для разности матриц правило аналогичное, необходимо найти разность соответствующих элементов.
Пример:
Найти
разность матриц 
, 
А
как решить данный пример проще, чтобы
не запутаться? Целесообразно избавиться
от лишних минусов, для этого внесем
минус в матрицу 
:
Примечание: в теории высшей математики школьного понятия «вычитание» нет. Вместо фразы «из этого вычесть это» всегда можно сказать «к этому прибавить отрицательное число». То есть, вычитание – это частный случай сложения.
5) Действие пятое. Умножение матриц.
Чем дальше в лес, тем толще партизаны. Скажу сразу, правило умножения матриц выглядит очень странно, и объяснить его не так-то просто, но я все-таки постараюсь это сделать, используя конкретные примеры.
Какие матрицы можно умножать?
Чтобы
матрицу 
можно
было умножить на матрицу 
нужно, чтобы
число столбцов матрицы
равнялось
числу строк матрицы
.
Пример:
Можно
ли умножить матрицу 
на
матрицу 
?
,
значит, умножать данные матрицы можно.
А вот если матрицы переставить местами, то, в данном случае, умножение уже невозможно!
,
следовательно, выполнить умножение
невозможно:
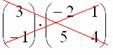
Не так уж редко встречаются задания с подвохом, когда студенту предлагается умножить матрицы, умножение которых заведомо невозможно.
Следует
отметить, что в ряде случаев можно
умножать матрицы и так, и так.
Например,
для матриц, 
и 
возможно
как умножение 
,
так и умножение 
Как умножить матрицы?
Умножение матриц лучше объяснить на конкретных примерах, так как строгое определение введет в замешательство (или помешательство) большинство читателей.
Начнем с самого простого:
Пример:
Умножить
матрицу 
на
матрицу
Я
буду сразу приводить формулу для каждого
случая:
–
попытайтесь
сразу уловить закономерность.
Пример сложнее:
Умножить матрицу на матрицу
Формула: 
В результате получена так называемая нулевая матрица.
Попробуйте
самостоятельно выполнить
умножение
(правильный
ответ 
).
Обратите
внимание, что 
!
Это почти всегда так!
Таким образом, при умножении переставлять матрицы нельзя!
Если
в задании предложено умножить матрицу 
на
матрицу 
,
то и умножать нужно именно в таком
порядке. Ни в коем случае не наоборот.
Переходим к матрицам третьего порядка:
Умножить
матрицу 
на
матрицу 
Формула
очень похожа на предыдущие формулы:
А теперь попробуйте самостоятельно разобраться в умножении следующих матриц:
Умножьте
матрицу
на
матрицу 
Вот готовое решение, но постарайтесь сначала в него не заглядывать!
