
- •1.Случайные события ,операции над событиями.
- •2.Вероятность случайного события и методы ее вычисления
- •3. Формулы комбинаторики Число сочетаний из n элементов по m
- •Перестановки из n элементов
- •Число размещений из n элементов по m
- •5. Относительная частота появления случайного события и ее вычисление
- •7.Теорема умножения вероятностей.
- •8. Формула полной вероятности
- •9.Формула Байеса
- •Задача 1
- •11. Основные числовые характеристики случайных величин их свойства
- •12. Математическое ожидание постоянной величины равно этой постоянной.
- •13. Дисперсия случайной величины
- •Формулировка[править | править исходный текст]
- •Доказательство
- •16. Закон равномерной плотности
- •17.Показательное распределение
- •18.Нормальное распределение
- •20. Числовые характеристики системы двух случайных величин
- •Корреляционный момент
- •2. Основные способы формирования выборочной совокупности
- •3. Определение необходимого объема выборки
- •4. Распространение результатов выборочного наблюдения на генеральную совокупность
- •4.1. Эмпирическая функция распределения.
- •4.2. Выборочная дифференциальная функция.
- •4.1. Точечная оценка параметров распределения
- •Линейная парная регрессия и метод наименьших квадратов
- •29.Система единичных векторов,свойства,базис,разложение по данному базису
- •32. Обратная матрица,ее свойства.Обращение матриц методом жордана-гаусса,условие обратимости матриц
- •Метод Гаусса—Жордана[править | править исходный текст]
- •С помощью матрицы алгебраических дополнений[править | править исходный текст]
- •Использование lu/lup-разложения[править | править исходный текст]
- •33.Элементарными преобразованиями матрицы
- •35. Векторная и матричная формы записи систем линейных уравнений Векторная форма записи
- •Матричная форма записи
- •36.Решение слау методом гаусса
- •Решение системы с помощью обратной матрицы
- •Определение[править | править исходный текст]
- •Свойства[править | править исходный текст] Инвариантность ранга при элементарных преобразованиях[править | править исходный текст]
- •Эквивалентность слау при элементарных преобразованиях[править | править исходный текст]
- •Нахождение обратных матриц[править | править исходный текст]
- •Приведение матриц к ступенчатому виду[править | править исходный текст]
- •39.Каноническая(предпочитаемая) форма записи слау
- •40.Симплексное преобразование слау
Линейная парная регрессия и метод наименьших квадратов
Парная
регрессия представляет собой уравнение,
описывающее связь между двумя переменными:
зависимой переменной
![]() и
независимой переменной
и
независимой переменной
![]() .
Иногда переменную
называют
результатом, а переменную
–
фактором:
.
Иногда переменную
называют
результатом, а переменную
–
фактором:
![]() ,
при этом функция может быть как линейной,
так и нелинейной. В данной главе более
детально рассмотрим линейную парную
регрессию. Предположим, что у нас есть
набор значений двух переменных
,
при этом функция может быть как линейной,
так и нелинейной. В данной главе более
детально рассмотрим линейную парную
регрессию. Предположим, что у нас есть
набор значений двух переменных
![]() Соответствующие
пары
Соответствующие
пары
![]() можно
изобразить на одной плоскости:
можно
изобразить на одной плоскости:
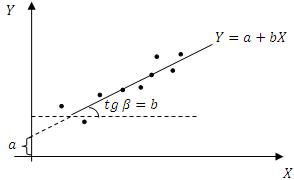
Параметр
![]() соответствует
отрезку прямой, отсекаемому линией
регрессии при пересечении с осью ординат,
параметр b определяет наклон линии
регрессии к оси абсцисс. При этом параметр
a традиционно принято называть свободным
членом регрессии, а параметр
соответствует
отрезку прямой, отсекаемому линией
регрессии при пересечении с осью ординат,
параметр b определяет наклон линии
регрессии к оси абсцисс. При этом параметр
a традиционно принято называть свободным
членом регрессии, а параметр
![]() –
коэффициентом регрессии, который
показывает, на сколько единиц в среднем
изменится значение
–
коэффициентом регрессии, который
показывает, на сколько единиц в среднем
изменится значение
![]() при
изменении
при
изменении
![]() на
одну единицу.
на
одну единицу.
Допустим,
что нашей задачей является подбор
функции
![]() из
параметрического семейства
функций
из
параметрического семейства
функций
![]() наилучшим
образом описывающая зависимость
наилучшим
образом описывающая зависимость
![]() от
от
![]() В
качестве меры отклонения функции
от
исходных наблюдений можно использовать:
В
качестве меры отклонения функции
от
исходных наблюдений можно использовать:
- сумму квадратов отклонений;
- сумму модулей отклонений;
- другие меры отклонений.
Согласно методу наименьших квадратов (МНК) неизвестные параметры модели выбираются таким образом, чтобы сумма квадратов отклонений эмпирических значений от модельных была минимальной:
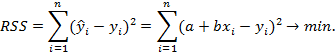
Среди преимуществ метода наименьших квадратов следует особенно отметить лёгкость вычислительной процедуры и хорошие по статистическим свойствам оценки. Данные факты объясняют широкое применение данного метода в статистическом анализе. Из недостатков наиболее существенным является – чувствительность к выбросам. Согласно необходимому условию экстремума функции нескольких переменных, необходимо найти частные производные по этим переменным и приравнять их к нулю. После ряда преобразований получим:
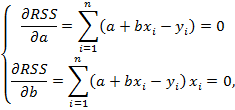
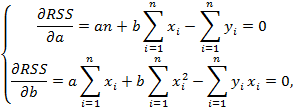
Разделим
обе части полученной выше системы на
![]() ,
получим систему нормальных уравнений:
,
получим систему нормальных уравнений:
![]()
![]()
Решив
полученную систему относительно
неизвестных параметров
![]() ,
получим:
,
получим:
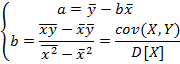
Таким образом, остатки, оцененные таким образом, можно представить следующим образом:
![]()
Свойства оценок МНК определяются предположениями относительно свойств случайного возмущения в модели наблюдений. Эти предположения обычно называются условиями Гаусса – Маркова.
Условия Гаусса-Маркова:
![]()
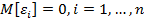 –
условие,
гарантирующее несмещённость оценок
МНК.
–
условие,
гарантирующее несмещённость оценок
МНК. –
условие
гомоскедастичности, его нарушение
приводит к проблеме гетероскедастичности.
–
условие
гомоскедастичности, его нарушение
приводит к проблеме гетероскедастичности.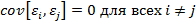 –
условие
отсутствия автокорреляции предполагает
отсутствие систематической связи между
значениями случайного члена в любых
двух наблюдениях. Если данное условие
не выполняется, то в модели возникает
проблема автокорреляции случайных
возмущений.
–
условие
отсутствия автокорреляции предполагает
отсутствие систематической связи между
значениями случайного члена в любых
двух наблюдениях. Если данное условие
не выполняется, то в модели возникает
проблема автокорреляции случайных
возмущений.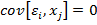 для
всех
для
всех
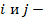 условие
независимости случайного возмущения
и объясняющей переменной. Значение
любой независимой переменной в каждом
наблюдении должно считаться экзогенным,
полностью определяемым внешними
причинами, не учитываемыми в уравнении
регрессии.
условие
независимости случайного возмущения
и объясняющей переменной. Значение
любой независимой переменной в каждом
наблюдении должно считаться экзогенным,
полностью определяемым внешними
причинами, не учитываемыми в уравнении
регрессии.
Достаточно
часто накладывают ещё одно условие на
остатки модели, но данное условие не
является условием Гаусса-Маркова:
![]() ,
оно очень полезно для проверки многих
гипотез.
,
оно очень полезно для проверки многих
гипотез.
Свойства оценок, полученных с помощью МНК:
Линейность оценок – оценки параметров и представляют собой линейные комбинации наблюдаемых значений объясняемой переменной
 .
.Несмещённость оценок:


Состоятельность оценок:
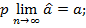

Эффективность – данное свойство означает, что оценка имеет минимальную дисперсию в заданном классе оценок:
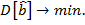
Теорема
Гаусса-Маркова: если
выполнены условия Гаусса-Маркова, тогда
оценки
![]() ,
полученные с помощью метода наименьших
квадратов, являются линейными,
несмещёнными, эффективными и состоятельными
оценками.
,
полученные с помощью метода наименьших
квадратов, являются линейными,
несмещёнными, эффективными и состоятельными
оценками.
Финансовой называется операция, начальное и конечное состояние которой имеют денежную оценку, и, цель проведения которой заключается в максимизации дохода в виде разности между конечной и начальной оценками. При этом практически все финансовые операции проходят в условиях неопределенности и, следовательно, их результат невозможно предсказать заранее. Поэтому при проведении финансовой операции возможно получение, как прибыли, так и убытка.
Поэтому, задача анализа доходности и риска финансовой операций заключается в оценке финансовой операции с точки зрения ее доходности и риска. Наиболее распространенным способом оценки финансовой операций является представление дохода операции как случайной величины и оценка риска операции как среднего квадратического отклонения этого случайного дохода.
Например,
если доход от проведения некоторой
финансовой операции есть случайная
величина ![]() ,
то средний ожидаемый доход
,
то средний ожидаемый доход ![]() –
это математическое ожидание случайной
величины
:
–
это математическое ожидание случайной
величины
:
![]() ,
,
Где ![]() есть
вероятность получить доход
есть
вероятность получить доход ![]() .
.
Т. к. среднеквадратическое отклонение
![]() ,
где
,
где ![]()
– это мера разбросанности возможных значений дохода вокруг среднего ожидаемого дохода, то его можно считать количественной мерой риска операции и обозначить как :
![]() .
.
Допустим,
что по четырем финансовым
операциям ![]() ,
, ![]() ,
, ![]() ,
, ![]() ряды
распределения доходов и вероятностей
получения этих доходов имеют вид:
ряды
распределения доходов и вероятностей
получения этих доходов имеют вид:
|
2 |
6 |
8 |
4 |
|
|
2 |
3 |
4 |
10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
1 |
2 |
8 |
|
|
0 |
4 |
6 |
10 |
|
|
|
|
|
|
|
|
|
|
|
Тогда, т. к. , то средний ожидаемый доход каждой операции имеет вид:
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Т. к. , то риски каждой финансовой операции имеют вид:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Нанесем
средние ожидаемые доходы
и
риски ![]() каждой
операции на плоскость (рис. 14.).
каждой
операции на плоскость (рис. 14.).

Рисунок 14 – Средние ожидаемые доходы и риски
Тогда, чем правее точка на графике, тем более доходная операция, чем точка выше – тем более она рисковая.
Для определения операции оптимальной по Парето, необходимо на графике найти точку, которую не доминирует никакая другая точка.
Так
как точка ![]() доминирует
точку
доминирует
точку ![]() ,
если
,
если ![]() и
и ![]() ,
то из графика на рисунке 14. видно, что
3-ая операция доминирует 2-ую операцию,
а 1-ая операция доминирует 3-ую и 2-ую
операции. Но 1-ая и 4-ая операции несравнимы,
т. к. доходность 4-ой операции больше, но
и риск ее тоже больше, чем доходность и
риск 1-ой операции, следовательно, 1-я
операция является оптимальной по Парето.
,
то из графика на рисунке 14. видно, что
3-ая операция доминирует 2-ую операцию,
а 1-ая операция доминирует 3-ую и 2-ую
операции. Но 1-ая и 4-ая операции несравнимы,
т. к. доходность 4-ой операции больше, но
и риск ее тоже больше, чем доходность и
риск 1-ой операции, следовательно, 1-я
операция является оптимальной по Парето.
Для
нахождения лучшей операции можно
применить взвешивающую формулу, которая
для пар ![]() дает
одно число, по которому можно определить
лучшую операцию. Допустим, что взвешивающей
формулой будет
дает
одно число, по которому можно определить
лучшую операцию. Допустим, что взвешивающей
формулой будет ![]() ,
тогда:
,
тогда:
|
|
Отсюда видно, что 1-ая финансовая операция – лучшая, а 2-ая – худшая.
28. векторы,их классификация,действия над ними,скалярное произведение
Вектор - относительно новое математическое понятие. Сам термин "вектор" появился в 1845 г. у ирландского математика Уильяма Гамильтона в работах по построению числовых систем. Гамильтону принадлежат такие термины как "скаляр", "скалярное произведение", "векторное произведение". В том же направлении проводили исследования английский математик Уильям Клиффорд и немецкий математик Герман Грассман. Клиффорд сумел объединить два подхода в рамках общей теории, включающей в себя и обычное векторное исчисление. Окончательный вид оно приняло в трудах американского физика и математика Джозайи Уилларда Гиббса, который в 1901 г. опубликовал обширный учебник по векторному анализу.
Вектор - это направленный отрезок, который имеет начало и конец. Понятие вектора возникает там, где приходиться иметь дело с объектами, которые характеризуются величиной и направлением.
К множеству векторов необходимо добавить еще один объект, который мы будем называть нулевым вектором. Его можно рассматривать как отрезок, у которого начало и конец совпадают. Длина такого вектора равна нулю, направления он не имеет. Все нулевые векторы равны друг другу. Так как нулевой вектор лежит на любой прямой, то, по определению, он считается коллинеарным любому вектору и перпендикулярным любому вектору.
В математической литературе векторы обозначаются обычно одним из следующих способов: . В двух последних случаях - обозначение точки, являющейся началом вектора, - концом вектора. Если же вектор нулевой, его принято обозначать нулем (0).
Так векторы выглядят на чертежах:
1.2 Определение векторов
Существует несколько видов определения векторов:
1. Два вектора называют равными, если их соответствующие координаты равны, или же они имеют одинаковую длину и направление (рис.3). Понятие равенства векторов позволяет отвлечься от расположения отрезка на плоскости или в пространстве и выделить длину и направление " в чистом виде".
2. Два вектора одинаковой длины, но противоположного направления, называются противоположными (рис.4). Вектор, противоположный вектору , обозначается через вектор .
3. Векторы называют коллинеарными если они лежат на параллельных прямых или на одной прямой (рис.5). Нулевой вектор считается коллинеарным любому вектору.
4. Три вектора считаются компланарными, если соответствующие им направленные отрезки расположены в одной плоскости или же в параллельных плоскостях (рис.6). Векторы компланарны только при условии что точки лежат в одной плоскости.
5. Длиной или модулем вектора называется длина соответствующего направленного отрезка, или расстояние между началом и концом вектора. Обозначается как или .
1.3 Действия над векторами
1.3.1 Сложение векторов
Суммой векторов и называется вектор .
Теорема: Каковы бы ни были точки А, В, С, имеет место векторное равенство .
Доказательство: Пусть , , данные точки. Вектор АВ имеет координаты , вектор ВС имеет координаты . Следовательно вектор АВ+ВС имеет координаты. А это и есть координаты вектора АС. Значит, векторы АВ+ВС и АС равны. Теорема доказана.
Свойства суммы векторов
1. Переместительное свойство: для любых векторов
2. Сочетательное свойство: для любых векторов .
3. Свойство нулевого вектора: для любого вектора
4. Существование и единственность противоположного вектора: для любого вектора существует, и притом только единственный, вектор , такой, что . Вычитание векторов - это операция обратная операции сложения. Вычесть из вектора вектор - значит найти такой вектор , который в сумме с вектором , даст вектор .
1.3.2 Скалярное произведение векторов
Скалярным произведение векторов и называется число .
Теорема: Скалярное произведение векторов равно произведению их абсолютных величин на косинус угла между ними.
,
где - угол между векторами.
Определение. Угол между двумя ненулевыми векторами - это величина образуемого ими угла, когда они отложены от одной точки. Угол между векторами не зависит от выбора той точки, от которой он откладываются:
Свойства скалярного произведения
1. , для любых векторов ;
2. для любых векторов и любого числа х;
3. для любых векторов ;
4. когда или хотя бы один из векторов нулевой;
5.
28.ЛИНЕЙНАЯ ЗАВИСИМОСТЬ ВЕКТОРОВ [vectors linear dependence] — частный случай по отношению к общему понятию линейной зависимости. Рассмотрим в качестве примера два произвольных ненулевых вектора, a и b, принадлежащих векторному пространствуV.
Если можно подобрать такие не равные нулю числа α и β, что αa + βb = 0, то векторы a и b называются линейно зависимыми. Причина этого ясна: с помощью полученного равенства можно выразить, напр., вектор a через вектор b. Это значит, что a зависит отb. Можно обобщить это определение и на произвольное число векторов: если существуют такие отличные от нуля числа α1, ..., αn, что ∑αiai = 0, то векторы называются линейно зависимыми, если же такая система чисел отсутствует, то линейно независимыми.
Линейное,
или векторное
пространство ![]() над полем
над полем ![]() —
это упорядоченная четвёрка
—
это упорядоченная четвёрка ![]() ,
где
,
где
![]() — непустое
множество элементов
произвольной природы, которые
называются векторами;
— непустое
множество элементов
произвольной природы, которые
называются векторами;
— (алгебраическое) поле, элементы которого называются скалярами;
![]() —
операция
сложения векторов, сопоставляющая
каждой паре элементов
—
операция
сложения векторов, сопоставляющая
каждой паре элементов ![]() множества
единственный
элемент множества
,
обозначаемый
множества
единственный
элемент множества
,
обозначаемый ![]() ;
;
![]() —
операция
умножения векторов на скаляры,
сопоставляющая каждому элементу
поля
и
каждому элементу
—
операция
умножения векторов на скаляры,
сопоставляющая каждому элементу
поля
и
каждому элементу ![]() множества
единственный
элемент множества
,
обозначаемый
множества
единственный
элемент множества
,
обозначаемый ![]() ;
;
причём, заданные операции удовлетворяют следующим аксиомам — аксиомам линейного (векторного) пространства:
 ,
для любых
,
для любых 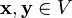 (коммутативность
сложения);
(коммутативность
сложения);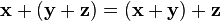 ,
для любых
,
для любых 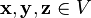 (ассоциативность
сложения);
(ассоциативность
сложения);существует такой элемент
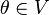 ,
что
,
что 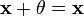 для
любого
для
любого  (существование
нейтрального элемента относительно
сложения),
в частности
не
пусто;
(существование
нейтрального элемента относительно
сложения),
в частности
не
пусто;для любого существует такой элемент
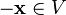 ,
что
,
что 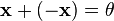 (существование
противоположного элемента относительно
сложения).
(существование
противоположного элемента относительно
сложения).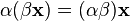 (ассоциативность
умножения на скаляр);
(ассоциативность
умножения на скаляр); (унитарность:
умножение на нейтральный (по умножению)
элемент поля F сохраняет вектор).
(унитарность:
умножение на нейтральный (по умножению)
элемент поля F сохраняет вектор).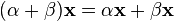 (дистрибутивность
умножения на вектор относительно
сложения скаляров);
(дистрибутивность
умножения на вектор относительно
сложения скаляров);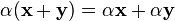 (дистрибутивность
умножения на скаляр относительно
сложения векторов).
(дистрибутивность
умножения на скаляр относительно
сложения векторов).
Таким образом, операция сложения задаёт на множестве структуру (аддитивной) абелевой группы.
Векторные пространства, заданные на одном и том же множестве элементов, но над различными полями, будут различными векторными пространствами.
В качестве дополнительной (девятой) аксиомы векторного пространства иногда используют следующую: размерность пространства равна некоторому натуральному числу (если существует максимальнаялинейно независимая система векторов данного пространства или, что тоже самое, существует конечная порождающая система векторов данного пространства), и тогда такое пространство называютконечномерным, или говорят, что пространство бесконечномерное (если не существует конечной порождающей системы векторов данного пространства). В соответствии с этим, теория линейных (векторных) пространств разделяется на две различные части: теорию конечномерных пространств, в которой существенным оказывается алгебраический аспект, и теорию бесконечномерных пространств, где главным оказывается аспект анализа — вопрос о разложимости данного элемента по заданной бесконечной системе функций.
Простейшие свойства[править | править исходный текст]
Векторное пространство является абелевой группой по сложению.
Нейтральный элемент является единственным, что вытекает из групповых свойств.
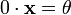 для
любого
.
для
любого
.Для любого противоположный элемент является единственным, что вытекает из групповых свойств.
 для
любого
.
для
любого
.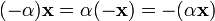 для
любых
для
любых 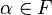 и
.
и
.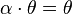 для
любого
.
для
любого
.
