20. Числовые характеристики системы двух случайных величин

Две случайные величины называются независимыми, если закон распределения одной из них не зависит от того, какие возможные значения приняла другая величина. Из этого определения следует, что условные распределения независимых величин равны их безусловным распределениям. Укажем необходимые и достаточные условия независимости случайных величин.

Теорема 5.1. Для того чтобы случайные величины   и   были независимыми, необходимо и достаточно, чтобы функция распределения системы   была равна произведению функций распределения составляющих:

Теорема 5.2. Для того чтобы непрерывные случайные величины   и   были независимыми, необходимо и достаточно, чтобы плотность вероятности системы   была равна произведению плотностей вероятностей составляющих:

Для описания системы двух случайных величин кроме математических ожиданий и дисперсий составляющих используют и другие характеристики, к которым относятся корреляционный момент и коэффициент корреляции.

Корреляционным моментом   случайных величин   и   называют математическое ожидание произведения отклонений этих величин:

Для вычисления корреляционного момента дискретных величин используют формулу

а для непрерывных величин

Корреляционный момент служит для характеристики связи между величинами   и  .

Теорема 5.3. Корреляционный момент двух независимых случайных величин   и   равен нулю.

Из теоремы 5.3 следует, что если корреляционный момент двух случайных величин   и   не равен нулю, то   и   — зависимые случайные величины.

Коэффициентом корреляции   случайных величин   и   называют отношение корреляционного момента к произведению средних квадратических отклонений этих величин:

Очевидно, коэффициент корреляции двух независимых случайных величин равен нулю (так как  ).

Корреляционный момент

Характеристикой зависимости между случайными величинами   и   служит математическое ожидание произведения отклонений   и   от их центров распределений (так иногда называют математическое ожидание случайной величины), которое называется корреляционным моментом или ковариацией:

Для вычисления корреляционного момента дискретных величин используют формулу:

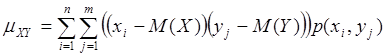
а для непрерывных величин – формулу:

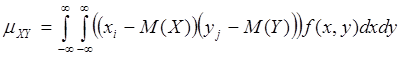
Эту формулу можно интерпретировать так. Если при больших значениях более вероятны большие значения, а при малых значениях   более вероятны малые значения  , то в правой части формулы положительные слагаемые доминируют, и ковариация принимает положительные значения.

Если же более вероятны произведения  , состоящие из сомножителей разного знака, то есть исходы случайного эксперимента, приводящие к большим значениям   в основном приводят к малым значениям   и наоборот, то ковариация принимает большие по модулю отрицательные значения.

В первом случае принято говорить о прямой связи: с ростом   случайная величина   имеет тенденцию к возрастанию.

Во втором случае говорят об обратной связи: с ростом   случайная величина   имеет тенденцию к уменьшению или падению.

Если примерно одинаковый вклад в сумму дают и положительные и отрицательные произведения  , то можно сказать, что в сумме они будут «гасить» друг друга и ковариация будет близка к нулю. В этом случае не просматривается зависимость одной случайной величины от другой.

Теорема. Корреляционный момент двух независимых случайных величин   и   равен нулю.

Доказательство. Так как   и   – независимые случайные величины, то их отклонения   и   также независимы. Пользуясь свойствами математического ожидания (математическое ожидание произведения независимых случайных величин равно произведению математических ожиданий сомножителей) и отклонения (математическое ожидание отклонения равно нулю), получим:

Ковариацию можно представить в виде:

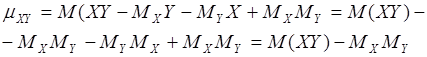
Из определения корреляционного момента следует, что он имеет размерность, равную произведению размерностей величин  и  . Другими словами, величина корреляционного момента зависит от единиц измерения случайных величин. По этой причине для одних и тех же двух величин величина корреляционного момента имеет различные значения в зависимости от того, в каких единицах были измерены величины. Такая особенность корреляционного момента является недостатком этой числовой характеристики, поскольку сравнение корреляционных моментов различных систем случайных величин становится затруднительным.

Для того, чтобы устранить этот недостаток, вводят новую числовую характеристику – коэффициент корреляции.

Коэффицие́нт корреля́ции или парный коэффицие́нт корреля́ции в теории вероятностей и статистике — это мера линейной зависимости двухслучайных величин.

ОпределениеПравить

Пусть   — две случайные величины, определённые на одном вероятностном пространстве. Тогда их коэффициент корреляции задаётся формулой:

,

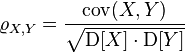где   обозначает ковариацию, а   —дисперсию, или, что то же самое,

,

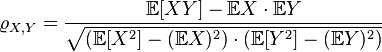где символ   обозначает математическое ожидание.

СвойстваПравить

• Неравенство Коши — Буняковского:

.

• Коэффициент корреляции равен 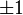  тогда и только тогда, когда 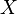  и 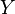  линейно зависимы:

,

где  . Более того в этом случае знаки   и   совпадают:

.

• Если   независимые случайные величины, то 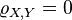 . Обратное, вообще говоря, неверно.

Статистическая совокупность - объект статистического изучении, состоящий из качественно однородных единиц, но отличающихся по каким-то другим признакам.

Генеральная совокупность - совокупность единиц, подлежащая изучению, ее численность обозначается N.

Выборочная совокупность - часть единиц генеральной совокупности, отобранная в случайном порядке, ее численность обозначается n. Выборочное наблюдение - не сплошное наблюдение, при котором обследованию подвергается оп­ределенная часть единиц изучаемой совокупности, отобранная в случайном порядке.

Преимущества выборочного наблюдения:

1) при обследовании слишком больших совокупно­стей, когда сплошное наблюдение требует огромных затрат труда и средств;

2) при необходимости получения информации в сжатые сроки;

3) при невозможности сплошного наблюдения.

Основные принципы выборочного наблюдения

1) обеспечение случайности - заключается в том, что при отборе каждой из единиц изучаемой совокупности обеспечивается равная возможность попасть в выборку

1) -обеспечение достаточного числа отобранных единиц.

Репрезентативность выборки - представительность отобранной из всей изучаемой совокупности части в отношении тех признаков, которые изучаются или оказывают влияние на формирование обобщающих характеристик.

Суть выборочного метода - получение первичных данных наблюдением выборки, анализом и их распространением на всю генеральную совокупность, с целью получения достоверной информации, об исследуемом явлении.

Характеристики генеральной совокупности - средняя, дисперсия, доля - называются генеральными и соответственно обозначаются х,  , р, где р - доля, отношение числа Мединиц, обладающих данным признаком, ко всей численности генеральной совокупности, т. е. р = М/N.

Обобщающие характеристики в выборочной совокупности называются выборочными и обозначаются соответственно x,  ,  , где   - частость, отношение числа единиц, обладающих данным признаком, в выборочной совокупности л, т.е.   = m/n.

Разность x - х=  _x, называется ошибкой репрезентативности выборочной средней, соответственно разность   - р =   называется ошибкой частости и разность   -   =  - ошибкой дисперсии.

Ошибка репрезентативности - расхождение между выборочной характеристикой и предполагаемой характеристикой генеральной совокупности.

Систематические ошибки репрезентативности - ошибки, возникающие в связи с особенностями принятой системы отбора и обработки данных на­блюдений или в связи с нарушением установленных правил отбора.

Случайные ошибки репрезентативности ошибки, возникающие в результате случайных различий между единицами, попавшими в выборку, и единицами генеральной совокупности.

Стандартная ошибка выборки:

Предельная ошибка выборки:   (t-коэффициент доверия).

Величина случайной стандартной и предельной ошибки зависит:

1) от принятого способа формирования выборочной совокупности;

2) от объема выборки;

3) от степени колеблемости изучаемого признака в генеральной совокупности.