3.10 Обработка результатов при многократном измерении одной и той же величины

Для определения параметров возьмем партию деталей, состоящей из n штук.

Измерим диаметр детали и, расположив их в порядке возрастания величин, получим ряд случайных дискретных величин.

Измерение значений (диаметров) наблюдаемых объектов называют парированием.

Если исследуемая функция принимает конечное значение, то ее называют дискретной.

Если она может принимать любые значения в некотором интервале, то ее называют непрерывной.

Расположение размеров в порядке возрастания или убывания называют ранжированием.

Число, показывающее сколько раз число встречается в ряде наблюдения, называют частотой и обозначают n.

Отношение частоты n к общему числу наблюдения N называют частностью

. (3.61)

А разность между наибольшим и наименьшим размерами называется размахом колебаний

. (3.62)

Для упрощения расчетов размах колебаний разбивают на к интервалов. Для определения оптимального значения величины интервалов h используют формулу Стейчжера

, (3.63)

(3.64)

Если k<8, то при дальнейших расчетах k=8.Если k>15, то k=15. Если 8<k<15, то принимают то, что получилось.

За начало первого интервала рекомендуется принимать величину

, (3.65)

за начало второго

. (3.66)

за начало третьего

(3.67)

Характер рассеивания значений случайной величины определяется гистограммой или эмпирической кривой, называемой полигоном, представленными на рисунке 3.11.

Рисунок 3.11- Гистограмма

Случайными величинами считаются размеры x_i, равные среднему арифметическому из диаметров каждого интервала. Тогда

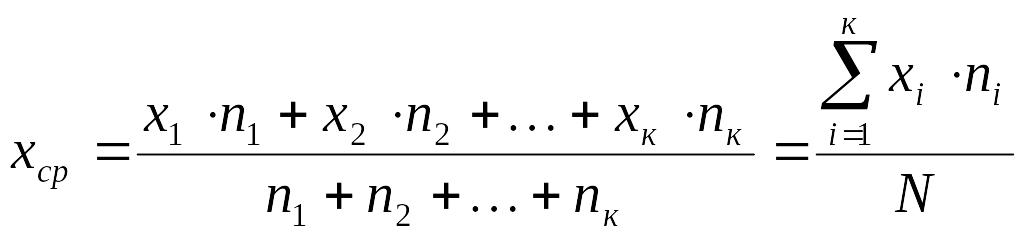, (3.68)

где x_i – среднее значение интервала, мм;

n_i – количество деталей в данном интервале.

Рассеивание значений относительно центра группирования характеризуется эмпирическим среднеквадратическим отклонением S .

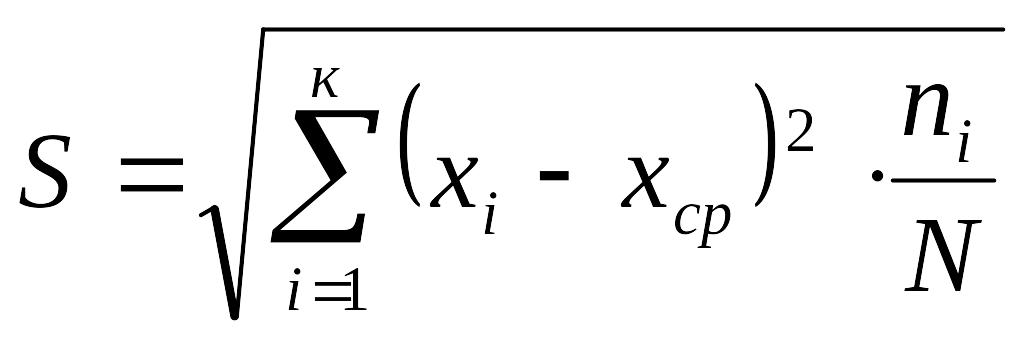. (3.69)

Эта формула справедлива, если число деталей в партии N<30. Если N>30, тогда

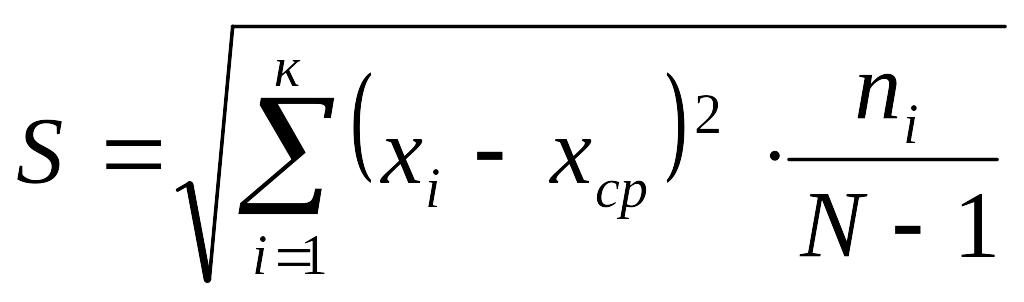. (3.70)

3.11 Статистическая проверка статистических гипотез

Полученные эмпирические данные необходимо подвергнуть статистическому анализу. Это делается с помощью выдвижения гипотез. Эта гипотеза может быть правильной или неправильной, поэтому возникает необходимость ее проверить. При проверке могут быть допущены ошибки двух родов. Первая заключается в том, что будет отвергнута правильная гипотеза. Вторая – что будет принята неправильная гипотеза.

Ошибку первого рода обозначают t_ – уровень значимости.

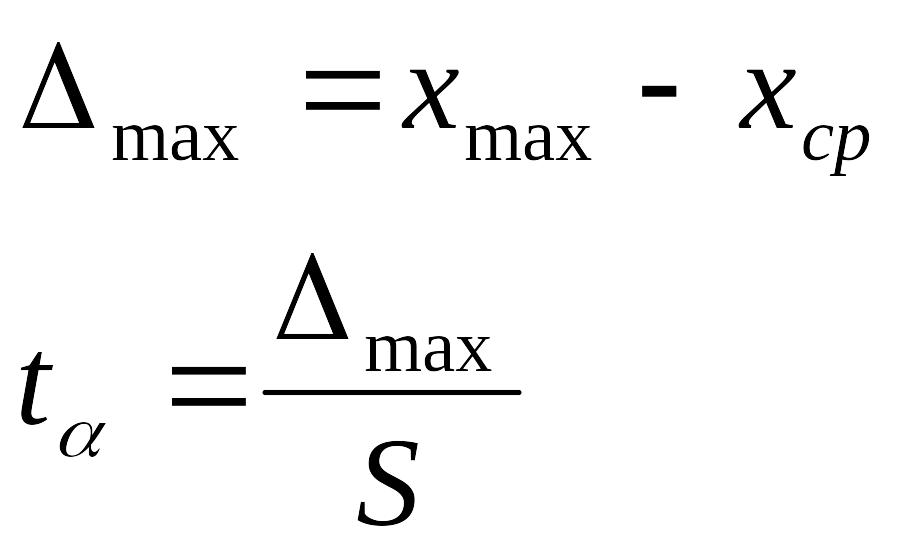. (3.71)

В таблицах приводятся численные значения критериев Стьюдента t(P, n).

Если действительное значение t_ меньше теоретического критерия Стьюдента, то считают, что наибольшее значение содержит грубую ошибку.

После исключения грубых ошибок выдвигают гипотезу о законах нормального распределения.

Часто в метрологии используют критерий Пирсона

, (3.72)

где k – количество интервалов;

n_i – количество деталей в i-том интервале,

N – общее количество деталей,

P_i – вероятность попадания в i-тый интервал.

Критерий Пирсена имеет число степеней свободы

, (3.73)

где z_i – левая граница i-того интервала, мм.

, (3.74)

где x_i – среднее значение i-того интервала, мм.

Левую границу наименьшего интервала z_i = z_min заменяют на (-). z_i = z_min-, а z_i = z_max+.

Если критерий Пирсена , то гипотеза о нормальном распределении случайной величины принимается.